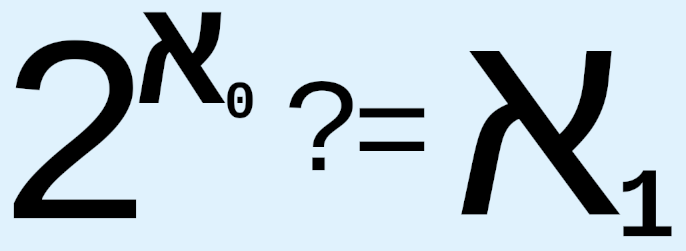After its initial development in the last quarter of the 19th century, Cantor’s theory of the infinite has grown to become an essential part of the now broadly-accepted standard version of set theory. But even in Cantor’s time, and since then into the present, various mathematicians and philosophers have rejected Cantor’s theory of the infinite as inherently flawed, on the ground that completed, that is, finitized, infinities cannot exist (e.g., the set of natural numbers ℕ = {1, 2, 3, 4, … } does not and cannot exist as a completed entity), and the terms finitism and constructivism – to the extent that these terms refer to coherent concepts – have been used to describe the philosophical position and mathematical practice which is based on the strong curtailing, and sometimes outright denial, of the logical legitimacy of what Cantor believed he had done, i.e., the finitizing of the infinite, though this curtailing and denial were more prominent a century ago. In fact, Cantor’s theory of the infinite is inherently flawed, and the flaw is based on a subtle confusion of concepts. At the heart of this confusion is the continuum hypothesis (CH), which, unlike much of standard set theory and broader mathematics, is not a statement that only indirectly and approximationally relies on the assumption of the existence of finitized infinity; rather, it depends directly and intrinsically on this assumption. As such, CH is directly affected by the flaw in Cantor’s theory of the infinite, and this difference shows itself in certain ways: for example, CH has remained unsolved for a more extended period of time than typical problems and questions in mathematics and set theory, and will remain so as long as the flaw in the foundations of the theory continues to be implicitly accepted as true. If a problem is foundational, rather than strictly mathematical, then every mathematical effort to resolve the problem will ultimately fail, because such effort will always be made in the context of the flawed foundation; and a foundation, being those most essential principles, patterns, and assumptions on which all other ideas and conclusions are based, is always the part of our thought, and our worldview, that we cling to most stringently, and is thus the part most difficult to recognize as flawed if it is flawed, and the most difficult to change, especially if nontrivial parts of that foundation are valid and lead to fruitful areas of research, correct conclusions about the natural world, and logically consistent and meaningful mathematical results.
When Cantor proposed CH in 1878, he expended extraordinary effort to try to provide an answer, but, as we know, he failed. Since then, various results related to CH have been obtained, such as Gödel’s 1938-40 proof that CH cannot be disproved from the axioms of ZFC and Cohen’s 1963 proof that CH cannot be proved from the axioms of ZFC, which, respectively, are meant to prove that CH is both logically consistent with and independent of the axioms of ZFC. Other results include using the axiom of determinacy to show that 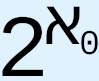 is not an aleph;1 that generalized CH entails the axiom of choice;2 that “the generalized continuum hypothesis is consistent with ZF ... and this result is stable under the addition of many large cardinal axioms”;3 that the axiom of constructibility implies generalized CH;4 the use of various large cardinal axioms, or, effectively, stronger axioms of infinity, that are tacked onto ZFC in order to propose the existence of larger and larger cardinals, such as “(in increasing order of size) strongly inaccessible, strongly Mahlo, measurable, Woodin, and supercompact cardinals,”5 in the hope that doing so will provide more information about the nature and structure of infinity, which we hope will in turn give us a greater chance of understanding and resolving CH and generalized CH; Woodin’s hypothesis known as the Star axiom, which would make
is not an aleph;1 that generalized CH entails the axiom of choice;2 that “the generalized continuum hypothesis is consistent with ZF ... and this result is stable under the addition of many large cardinal axioms”;3 that the axiom of constructibility implies generalized CH;4 the use of various large cardinal axioms, or, effectively, stronger axioms of infinity, that are tacked onto ZFC in order to propose the existence of larger and larger cardinals, such as “(in increasing order of size) strongly inaccessible, strongly Mahlo, measurable, Woodin, and supercompact cardinals,”5 in the hope that doing so will provide more information about the nature and structure of infinity, which we hope will in turn give us a greater chance of understanding and resolving CH and generalized CH; Woodin’s hypothesis known as the Star axiom, which would make 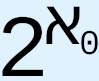 equal to
equal to 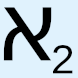 , invalidating CH, though “Woodin stated in the 2010s that he now instead believes CH to be true, based on his belief in his new ‘ultimate L’ conjecture”;6 the result of Saharon Shelah that “was able to reverse a trend of fifty years of independence results in cardinal arithmetic, by obtaining provable bounds on the exponential function. The most dramatic of these is
, invalidating CH, though “Woodin stated in the 2010s that he now instead believes CH to be true, based on his belief in his new ‘ultimate L’ conjecture”;6 the result of Saharon Shelah that “was able to reverse a trend of fifty years of independence results in cardinal arithmetic, by obtaining provable bounds on the exponential function. The most dramatic of these is 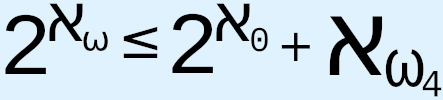 . Strictly speaking, this does not bear on the continuum hypothesis directly, since Shelah changed the question and also because the result is about bigger sets. But it is a remarkable result in the general direction of the continuum hypothesis”;7 the fact that Martin’s Axiom for
. Strictly speaking, this does not bear on the continuum hypothesis directly, since Shelah changed the question and also because the result is about bigger sets. But it is a remarkable result in the general direction of the continuum hypothesis”;7 the fact that Martin’s Axiom for 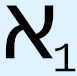 , i.e.,
, i.e., 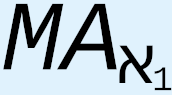 , "implies
, "implies 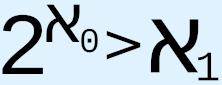 , the negation of the Continuum Hypothesis”;8 and many others. But results such as these either assume CH or generalized CH to be true in order to see what results follow from this assumption, or else take for granted that different levels of infinity exist and that infinite sets can be treated, a la Cantor, as finite, complete, conceptually concrete, mathematically manipulable entities. In the first case, if CH itself is a logically flawed statement, then one cannot prove the truth or falsity of CH by first assuming its truth or falsity, since no amount of logical deduction from this starting point will lead to valid logical conclusions that can be identified with valid logical conclusions from other areas of mathematics; also, since such comparisons, should we attempt to make them anyway, would depend on the validity of these other conclusions, they would be regressivist in nature and so subject to the potential uncertainties involved in regressivist arguments. In the second case, as we shall see, the assumption that infinity can be finitized is flawed, which means that mathematical investigations that are based on this assumption will always fail to resolve the continuum hypothesis.
, the negation of the Continuum Hypothesis”;8 and many others. But results such as these either assume CH or generalized CH to be true in order to see what results follow from this assumption, or else take for granted that different levels of infinity exist and that infinite sets can be treated, a la Cantor, as finite, complete, conceptually concrete, mathematically manipulable entities. In the first case, if CH itself is a logically flawed statement, then one cannot prove the truth or falsity of CH by first assuming its truth or falsity, since no amount of logical deduction from this starting point will lead to valid logical conclusions that can be identified with valid logical conclusions from other areas of mathematics; also, since such comparisons, should we attempt to make them anyway, would depend on the validity of these other conclusions, they would be regressivist in nature and so subject to the potential uncertainties involved in regressivist arguments. In the second case, as we shall see, the assumption that infinity can be finitized is flawed, which means that mathematical investigations that are based on this assumption will always fail to resolve the continuum hypothesis.
Other researchers take a different approach. For example, Solomon Feferman has argued that CH is not decidable, based on the idea that the concept of an arbitrary set of the reals – or any set with the same cardinality – is inherently vague and cannot be made more precise without violating the nature of an arbitrary set; and since the meaning of CH is tied to the concept of an arbitrary set of reals, CH is not a precise enough statement to have a truth value.9 Let us examine this argument more closely, as well as certain other things Feferman says in his writings on the subject. For example, Feferman states, “Levy and Solovay (1967) showed that CH is consistent with and independent of all such large cardinal assumptions, provided of course that they are consistent. So the assumption of even (Large) Large Cardinal Axioms (LLCAs) is not enough; something more will be required.”10 This is another indication, however indirect, that there is something different about CH when compared to many other problems in set theory. Feferman describes a certain perception among set theorists regarding CH: “There is no disputing that CH is a definite statement in the language of set theory, whether considered formally or informally. And there is no doubt that that language involves concepts that have become an established, robust part of mathematical practice. Moreover, many mathematicians have grappled with the problem and tried to solve it as a mathematical problem like any other. Given all that, how can we say that CH is not a definite mathematical problem?”11 He further states that “one can try to sidestep [difficult issues in trying to finitize infinity] by posing the question of CH within an axiomatic theory T of sets, but then one can only speak of CH as being a determinate question relative to T.”12 Notice the use of the phrases “in the language of set theory” and “relative to T,” which imply that CH can be thought of as a meaningful question within the context of a set theory that already assumes that it is possible to finitize the infinite, i.e., that it is meaningful to use and manipulate a symbol that represents infinity, such as ω or 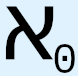 , in the same way that we would use and manipulate symbols that represent finite quantities. Feferman’s assessment is correct here, and more will be said about this later. Further, in discussing the modeling of large cardinals and the components of CH in second-order logic, Feferman states, “Clear as these results are as theorems within ZFC about 2nd order ZFC, they are evidently begging the question about the definiteness of the above conceptions required for the formulation of CH… . But in relying on so-called standard 2nd order logic for this purpose we are presuming the definiteness of the very kinds of notions whose definiteness is to be established.”13 (Italics mine.) Again, this is correct: arbitrarily assuming that a concept is clear and definite, and using it as if it is, does not make it so. Feferman further states, “But it is an idealization of our conceptions to speak of 2ℕ, resp. S(ℕ) [the power set of ℕ], as being definite totalities. And when we step to S(S(ℕ)) there is a still further loss of clarity, but it is just the definiteness of that that is needed to make definite sense of CH.”14 (Italics mine.) This is also correct, as Feferman points to the incorrectness of the idea that we can treat infinities as finite things, and at least implies that there is inherent, i.e., ineradicable, vagueness in the conception of multiple levels of infinity; and he also points to the fact that logical validity and clarity of concepts is needed in precisely these things if the statement of CH is to be meaningful, and therefore to have an objective truth value (and not just a truth value in the context of an arbitrary set-theoretical framework which already assumes that infinities can be treated as finite quantities and that there are multiple levels of infinity). Again, more on this later.
, in the same way that we would use and manipulate symbols that represent finite quantities. Feferman’s assessment is correct here, and more will be said about this later. Further, in discussing the modeling of large cardinals and the components of CH in second-order logic, Feferman states, “Clear as these results are as theorems within ZFC about 2nd order ZFC, they are evidently begging the question about the definiteness of the above conceptions required for the formulation of CH… . But in relying on so-called standard 2nd order logic for this purpose we are presuming the definiteness of the very kinds of notions whose definiteness is to be established.”13 (Italics mine.) Again, this is correct: arbitrarily assuming that a concept is clear and definite, and using it as if it is, does not make it so. Feferman further states, “But it is an idealization of our conceptions to speak of 2ℕ, resp. S(ℕ) [the power set of ℕ], as being definite totalities. And when we step to S(S(ℕ)) there is a still further loss of clarity, but it is just the definiteness of that that is needed to make definite sense of CH.”14 (Italics mine.) This is also correct, as Feferman points to the incorrectness of the idea that we can treat infinities as finite things, and at least implies that there is inherent, i.e., ineradicable, vagueness in the conception of multiple levels of infinity; and he also points to the fact that logical validity and clarity of concepts is needed in precisely these things if the statement of CH is to be meaningful, and therefore to have an objective truth value (and not just a truth value in the context of an arbitrary set-theoretical framework which already assumes that infinities can be treated as finite quantities and that there are multiple levels of infinity). Again, more on this later.
But then Feferman reverts to using familiar concepts from set theory and logic to propose (the beginning of) a solution. However, he breaks somewhat from the traditionalist set-theoretical assumption which says that all of set theory can be based on the concepts of classical logic, i.e., the system of logic in which the Law of the Excluded Middle (LEM) is assumed to be always applicable. In particular, he makes use of the ideas of intuitionistic logic, in which LEM is not taken as a universal given, to define “semi-intuitionistic” and then “semi-constructive”15 versions of set theory in which the truth of statements about quantification over definite or non-vague sets or collections is settled by classical logic, while the truth of statements that quantify over non-definite or inherently vague sets or collections, or perhaps uncountable collections, may possibly be settled by intuitionistic logic. He asks of the “statements of classical set theory that are of mathematical interest, one would like to know which of them make essential use of full non-constructive reasoning and which can already be established on semi-constructive grounds.”16 Finally, Feferman says that CH is a meaningful statement in the context of his modification of set theory that he calls SCS + (Pow(ω)), which is his semi-constructive set theory with the axiom of power set added but restricted to the power set operation only of the lowest level of infinity; and then he says that CH is a definite statement, which presumably means that it has a definite truth value in some sense, in the context of his SCS + (Pow), which is his semi-constructive set theory with the full axiom of power set added, i.e., the axiom of power set as applied to all levels of infinity. Then he states that the concept of the power set of ω is “clear enough,”17 but that the concept of an arbitrary subset of this power set is not clear, and that it is precisely this lack of conceptual clarity that makes CH an “essentially vague statement, which says something like: there is no way to sharpen it to a definite statement without essentially changing the meaning of the concepts involved in it.”18
Feferman sees the truth through a glass darkly. He understands that there is some sort of essential vagueness in the statement of CH, but he does not provide any real clarity on the nature and source of this vagueness. Feferman writes, “Presumably, CH is not definite in SCS + (Pow(ω)), and it would be interesting to see why that is so.”19 In other words, presumably his semi-constructive set theory with the power set operation restricted to the power set of the lowest level of infinity cannot contain a definite statement of CH about which we could draw some kind of definite conclusion, which possibly makes intuitive sense given that CH relates the lowest level of infinity to the next higher level of infinity, and perhaps just like first-order logic Feferman’s Pow(ω) operation does not encompass the next higher level of infinity in a way that makes it “useful” in making a definite statement about CH; however, there is a certain lack of clarity in Feferman’s statement, in that, given Cantor’s theorem that the cardinality of a set is always strictly less than the cardinality of its power set, and since the cardinality of the set ω is the cardinality of the infinite set of natural numbers, this means (in standard set theory) that the cardinality of Pow(ω) must be strictly greater than the cardinality of ω; and since Pow(ω) is included as a valid entity in Feferman’s SCS + Pow(ω) set theory, isn’t SCS + Pow(ω) itself already powerful enough to make at least CH “definite,” if not generalized CH? But this lack of clarity, as will be shown, is itself a symptom of an insufficient grasp of both the nature of infinity and the nature of the uncountable, and, in particular, of the nature of the supposed difference between countable and uncountable infinity as represented most memorably by Cantor’s famous diagonal argument.
In his concluding statement that CH is inherently vague, Feferman says, “But to formulate that idea more precisely within the semi-constructive framework, some stronger notion than formal definiteness may be required.”20 This is correct, but likely not in the way Feferman thinks. Feferman states that he is interested in finding a more precise formulation of the vagueness of CH “within the semi-constructive framework,” and the implication is that by using intuitionistic logic in the right way, we may be able to formulate the notion of “vagueness” in a precise manner, i.e., in the form of mathematical symbolism, and with this precise expression of vagueness we may be able to settle CH in a satisfactory way, and, in particular, to prove that CH is inherently vague. But there is a problem here, and it is in the incorrect understanding of the value and usefulness of intuitionistic logic. Intuitionistic logic cannot “settle” the truth of any idea, i.e., it cannot draw definitive conclusions about something – if it could, it would be no different from classical logic. At best, intuitionistic logic can only be used to provide a formal mathematical or symbolic representation of our lack of knowledge about something. Assuming a statement is based on clear (i.e., not vague) concepts, then the more knowledge we gain about the subject matter of the statement, the closer we come to being able to determine definitively whether the statement is true or not, i.e., to determine its truth value classically. There are many statements, such as typical statements about the natural world in science, whose truth value may never be definitively determined in the sense of classical logic no matter how much we know about such a statement’s subject matter, and no matter how confident we are in such a statement’s truth (e.g., the statement “gravity is always an attractive force”), and in this sense we can say that we may never be able to determine the truth value of such a statement in the classical sense. In such a case, we may represent our lack of perfect knowledge using intuitionistic formalism, but doing so does not increase our knowledge beyond what we already had before we took recourse to the intuitionistic formalism. At best, it provides us with a false sense that we have gained knowledge in some way by representing our current lack of knowledge more concretely. This is the case in general when the methods of intuitionistic logic are applied to a statement, and in particular to CH. If CH is inherently vague, as Feferman claims, then perhaps we may be able to represent this vagueness “more concretely” by the methods of intuitionistic logic, but such concretization in no way gives us a clearer understanding of the nature and source of the vagueness; at best, it gives us a false sense of having gained knowledge about the statement being analyzed, because we have invested a nontrivial amount of thought to produce the result, and have manipulated symbols into a form they were not in before, all of which is certainly an achievement, just not the particular achievement we sought. This is not to mention the fact that Feferman’s system of set theory itself already includes at least Pow(ω) as part of its axiomatic framework, and so ω and Pow(ω), which are infinite quantities, are from the beginning being treated in certain ways by Feferman’s system as finite, mathematically manipulable quantities, which, as Feferman indirectly indicates when he says that the concepts underlying CH are inherently vague, is a starting point for flaws, blind spots, and self-imposed limitations on our thinking about and understanding of the subject matter. Given these considerations, though Feferman’s assessment that CH cannot be given a definite truth value is correct, his approach to finding the reason for this will ultimately fail no less than the approach of appending ever stronger axioms of infinity to ZFC in the hope that by doing so we will learn more about the “hierarchy of infinities” and be able thus to use this new knowledge to finally resolve CH. In both cases, though in different ways, the reasoning is based on the unsubstantiated assumption of the validity of the very concepts that make CH vague and that prevent it from having a definite truth value. Such proposals still fall back on the flawed but familiar conceptions of completed infinite sets and different levels of infinity, even in the context of the recognition that there is a flaw in the notion of completed infinity, as in Feferman’s case, and the reason we still fall back on these flawed but familiar conceptions is simply that in our effort to grasp infinity, and to finally resolve CH, we can think of nothing better to put in their place.21
In a later article,22 Feferman again makes certain statements that show he is on the right track, but also that he still does not see how the different pieces fit together. Specifically, he says, “Briefly, mathematics at bottom deals with ideal world pictures given by conceptions of structures of a rather basic kind. Even though features of those conceptions may not be clearly definite, one can act confidently and go quite far as if they are; the slogan is that a little bit goes a long way. Nevertheless, if a concept such as the totality of arbitrary subsets of any given infinite set is essentially indefinite, we may expect that there will be problems in whose formulation that concept is central and that are absolutely unsolvable. We may not be able to prove that CH is one such ... but all the evidence points to it as a prime candidate.”23 Feferman’s general statement regarding indefiniteness and unsolvable problems is correct, and, as with some of Feferman’s other commentary on the CH issue, it touches upon the core of the problem, yet again without providing any clarity on the source of the indefiniteness in the case of CH. He then goes on to outline his proposed logical framework based on intuitionistic logic by which we may possibly be able to formally prove that CH is indefinite, and thus cannot be assigned a truth value. The framework he outlines in this newer article is no different from that outlined in his older article. However, he does report a new result, specifically that “Rathjen (2014) established my conjecture using a quite novel combination of realizability and forcing techniques.”24 He then goes on to describe certain additional consistency and broader set-theoretic applicability results of Rathjen’s finding, and implies that this finding perhaps makes things more manageable by stating that whereas earlier results ω1 or infinitely many Woodin cardinals, Feferman’s and Rathjen’s work shows that similar results can be obtained by the much smaller infinite value of Pow(ω). Feferman concludes with, “I do not claim that his work proves that CH is an indefinite mathematical problem, but simply take it as further evidence in support of that. Moreover, it shows that we can say some definite things about the concepts of definiteness and indefiniteness when relativized to suitable systems; these deserve further pursuit in their own right.”25 We must note here for emphasis that Feferman does not claim to have actually understood the source of the vagueness that is inherent in CH, only that certain results in the context of his SI version of set theory reinforce his belief that the inherent vagueness is real, by supporting the idea, via Rathjen’s 2014 work, that CH is not “definite” in the context of his version of set theory, i.e., that CH cannot be resolved in the context of his version of set theory in terms of classical logic, and, therefore, at best CH’s inherent vagueness can be formally stated in the context of his system’s implementation of intuitionistic logic. But as Feferman himself suggests, this does no more than provide an additional hint that his sense that CH is vague is correct, and does nothing to touch upon the underlying reason for the vagueness, which it is necessary to understand in order to actually resolve CH. As stated above, intuitionistic logic can do no more than provide a formal symbolic expression of our lack of knowledge about something. As such, it cannot be used to directly prove the truth or falsity of any statement. In other words, for any system of logic, whether intuitionistic, classical, or otherwise, the only possible way to prove something is to draw logically valid deductions based on logically valid premises. But in the case that one is able to do this, one has no need for what intuitionistic logic offers, i.e., one is able to state one’s result definitively, in the context of classical logic, that is, in the context of a system of logic that treats LEM as a universal given. Only if one does not have a clear understanding of the subject matter might one think that intuitionistic logic could be useful, in order to perhaps “clarify” one’s lack of understanding. But the reality is that the idea of intuitionistic logic being able to definitively prove anything, including that a particular statement is inherently vague or indefinite, is a contradiction in terms; definitive proof precludes the very nature of and need for intuitionistic logic.
Feferman also makes a comparison between standard set theory and his semi-intuitionistic and semi-constructive versions of set theory (which he call KPω, SI-KPω, and SC-KPω, respectively), and with regard to these he states, “The main result in [one of Feferman’s 2010 articles on the subject] is that all of these systems are of the same proof-theoretical strength… . Moreover, the same result holds when we add the power set axiom Pow as providing a definite operation on sets, or just its restricted form Pow(ω) asserting the existence of the power set of ω.”26 Okay. But note that this is a regressivist argument, not an argument for the independent, i.e., objective, validity of Feferman’s set-theoretic axiomatic constructions; furthermore, the truth of this argument depends on the validity of the axioms and framework of proof theory. Feferman’s result simply states that according to proof theory his SI and SC constructions of set theory and standard ZFC are equiconsistent. In other words, this result is an indication that Feferman’s constructions of set theory accurately mirror standard set theory in essential ways, so that results obtained in Feferman’s constructions, at least in regard to those things which standard set theory covers, may perhaps be treated as valid in standard set theory as well. Such an equivalence should not be construed as providing any reason to believe that Feferman’s constructions of set theory are more true, more accurate, or, in particular, more capable of solving CH, than any other known variant of set theory; at best, we may say that this result shows that nothing in Feferman’s constructions of set theory will explicitly contradict any of the statements of standard set theory.
As stated at the beginning, there is a confusion of concepts that is at the center of why CH is so difficult to resolve. As such, if we take some time to clarify these concepts, we can understand the source of the confusion and provide a satisfactory resolution to CH and generalized CH. It should be noted at this point that certain of the concepts and descriptions to follow will be unorthodox from a traditional mathematical point of view. It should also be noted that certain of the concepts and descriptions to follow may initially seem to be within a certain philosophical tradition, such as, in particular, constructivism or finitism, but the reader, especially one whose philosophical inclinations lean in an opposing direction, is asked to be patient and allow the explanation to proceed to the end without resort to any prior understanding of the often confusing and contradictory natures of the variants of a particular philosophical tradition which this paper may seem to be espousing. For a problem such as CH, which has been resiliently opaque and intractable for such a long time, it should be expected that it will be necessary to resort to certain unorthodox ideas, and certain reinterpretations of familiar ideas, in order to find a resolution. That being said, the argument to follow does not employ any complicated or extensive set-theoretic or mathematical formalism; as a result, it is relatively easy to follow, even for those not schooled in set theory or advanced mathematics.27 And this, too, is expected. When clarity is obtained on a subject, it becomes much easier to understand its essential nature (this itself is what it means to obtain clarity about something), and it is also easier to see when an argument on the subject is off base, or based on flawed assumptions, or will not achieve the desired end. As a result, explanation can be simplified.
We will begin with a basic discussion about the nature of infinity. Infinity is the quality of being not finite, i.e., it is the opposite of “finite,” and this understanding is implicit in important ways in much of mathematical thought, though in other ways it is not. As such, we may understand that if we take a sequence of numbers defined by an easily recognizable pattern, such as the sequence 1, 2, 3, 4, … which is produced by what in set theory is called the successor function, and stop this iteration at any point, we are left with a finite, i.e., a non-infinite, collection of numbers, no matter how large. Such a finite collection of numbers is a finished thing, and it is thus possible to conceive, without logical contradiction, that a single entity, which we may call a set (or otherwise a collection, group, class, or any other similar term), explicitly contains every single one of these items, and, further, that since the number of items is finite, the set itself is finite in extent as well, i.e., it is bounded or circumscribable in a meaningful sense of these terms. Note that “extent” does not necessarily mean spatial extent; in the case of this example it means conceptual extent, though the two are inherently related.28 However, the same argument can be made for such a collection of items or objects in physical space – say, billiard balls: no matter how many billiard balls are added to our collection of billiard balls (assume they are added one at a time, though this is not strictly necessary), if we stop at any point, we have a finite collection of billiard balls taking up a finite amount of space, i.e., having a finite extent in space, no matter how large. As such, it is not a logical contradiction to say that such a collection is fully bounded or circumscribable.
However, this is not the case with the infinite. In fact, it cannot be the case, because by definition “infinite” means “not finite” – any other definition of this term would make it devoid of meaning. Therefore, for a “set” or “collection” to be infinite one would have to not stop at any point in the addition of further items or objects, whether in conceptual space or in physical space.29 This means that an infinite “set” would have the characteristic of being not bounded and not circumscribable in any meaningful sense of these terms. It is therefore a logical contradiction, and therefore an impossibility, to have a finite object, such as a set or collection that we treat in our thought and mathematical manipulations as a bounded or circumscribable or complete entity which can, for example, have relations of various kinds with other such entities and can itself be a member of other such entities, be an infinite quantity. At most we may represent an infinite quantity by a finite symbol, such as ℕ to represent the infinite quantity of the natural numbers, or call this never-ending collection of elements a “set” or an “infinite set,” in order to make our thought about these collections and our mathematical manipulations in certain ways more convenient. There is no logical contradiction in a representation. The problems begin when we start treating this practical conceptual tool as if it were a concrete reality (either conceptually or physically); in doing so, we stretch this practical tool beyond the bounds of its applicability. When this is done, subsequent results will have logical flaws in them, and questions and statements of problems that are made on the basis of this concretization will have the remarkable ability to resist all efforts at solution decade after decade and remain, essentially, always just as opaque and intractable as when they were first articulated. It is this subconscious stretching of a practical conceptual tool beyond the bounds of its applicability that, gradually over time, allows us to become comfortable with the idea that an infinite quantity can actually be a finite, manipulable, bounded, circumscribable thing, that, in other words, there is no contradiction in such a conception, or else helps us develop a mental framework within which we can, for all practical purposes, forget that there is a contradiction, or treat the contradiction as insignificant.30 Part of understanding why CH has not yet been solved in all this time is to backtrack on this concretization in order to return to an accurate understanding of the limitations that should be placed on the use of finite symbols, such as ℕ or 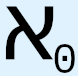 , to represent infinite quantities. It will also be of benefit to come to a better understanding of why there is such a strong desire to make these concretization efforts in the first place, which understanding will make us better able in the future to prevent such concretization from happening, or to recognize sooner when it is happening.31
, to represent infinite quantities. It will also be of benefit to come to a better understanding of why there is such a strong desire to make these concretization efforts in the first place, which understanding will make us better able in the future to prevent such concretization from happening, or to recognize sooner when it is happening.31
Let us now take a moment to reexamine, in light of the preceding discussion, certain key aspects of the items in standard set theory known as cardinals and ordinals. We will also discuss here the concepts of transfinite induction and transfinite recursion. First, we understand that in standard set theory, “Every natural number is an ordinal.”32 We also understand that in standard set theory, “Finite sets can be defined as those sets whose size is a natural number… . By our definition, cardinal numbers of finite sets are the natural numbers.”33 So the definitions of ordinal number and cardinal number include the natural numbers. The difference between the two is that ordinal numbers are the numbers themselves as entities or objects (typically envisioned as being written in order from smaller to larger), and cardinal numbers are the magnitude or size of each ordinal number. For the natural numbers, i.e., the finite quantities, the ordinal and its corresponding cardinal always match, e.g., the ordinal 2 has magnitude, or size, 2; this is, however, not always the case with ordinals and cardinals that are infinite. In set theory, it is common practice to “extend” the sequence of natural numbers into what is called the transfinite, i.e., beyond the finite. It is imagined that we may use a symbol to represent the ordinal number that is one unit beyond the “end” of the natural numbers, and in standard set theory the symbol typically used for this is ω. At first this may seem counterintuitive, but one may accustom oneself to the idea by analogy with how each finite number is merely one unit beyond the end of the sequence of all smaller finite numbers. Also, the idea of an “end” of the natural numbers can be made more palatable by equating ℕ to ω, i.e., defining ω = ℕ, since ℕ is another symbol used to represent the natural numbers as a whole, i.e., we are already accustomed to the idea that ℕ represents an infinite quantity. But once we have grown accustomed to this idea, it is not so great a leap to the idea that we may “extend” the arithmetic operation of addition by one, i.e., of the successor function, which is a well-defined notion in the context of finite numbers, into the transfinite, and thus that it is meaningful to define the quantity ω+1; and once we are at this point, it is easy to see how the same algorithm may be applied again, since 1 is a finite number, and it is well understood how to increase a finite number by one. We therefore must do very little at this point conceptually to convince ourselves that it is meaningful also to define the quantities ω+2, ω+3, ω+4, etc. But this is now clearly a pattern, and since the first ω is defined as the number right after the “final” number of the natural number sequence, we convince ourselves that it is meaningful to take the second term in these transfinite expressions all the way to ω as well and define the transfinite “number” ω+ω, which is also represented as ω⋅2, i.e., the scalar product of ω and 2.34 In this way, we can then define subsequent expressions, such as ω⋅3, ω⋅4, … ω⋅ω = ω2, ω2 + 1, ω2 + 2, … ωω … ωω+1 … ωω2 … ωωω ... ωωωω … .35 But we can go beyond this. We can say that the number after the very “end” of this infinite sequence of transfinite ordinals can be represented by another letter, say ɛ, and then proceed down the same road with ɛ, creating ɛ+1, ɛ+2, etc.36 It is clear that this process can never end, because it is always possible to take the very “end” of whatever sequence of transfinite numbers we are looking at (in set theory this would be called the sequence’s supremum), arbitrarily denote the number “after” this by yet another finite symbol, and start the pattern of increase all over again from that yet “higher” point. We don’t even have to use symbols that are in any of the known alphabets. We could use a glibbor, a letter in a made-up alphabet that no human civilization has ever used and whose symbolic form is a character unfamiliar to anyone in history. We could keep making up new symbols and alphabets after we had exhausted all the known ones, and continue this process until we are blue in the face and our chairs and our desks have completely fused with our bodies, and we still would not have reached, nor could we ever reach, an actual end. The process of evaluating these expressions is known as ordinal arithmetic, which is widely accepted as a valid practice in standard set theory. Nonetheless, the process of ordinal arithmetic is a prime example of what can be called pathological behavior, if we modify the definition a little to say that “pathological” means “an outgrowth, or a symptom, of one or more flawed premises,” rather than what it sometimes means, viz., “a counterintuitive mathematical result that is a symptom of a certain amount of imprecision in one’s founding definitions of one or more terms.” What has caused this pathological behavior is the initial assumption that it is possible, and not logically contradictory, for there to be an “end” to the sequence of natural numbers. Once we deny that there is a logical contradiction here, we may begin to treat this infinity, which here we call ω, as if it is a finite number, which can then be the subject of arithmetic operations. But this is logically impossible, because the sequence of natural numbers is infinite, i.e., not finite, and so there is, and can be, no end to the sequence, no “greatest” or “last” number in the sequence. This then means that there can be no number “beyond the end” of the sequence, and, in particular, that the term ω as used in standard set theory, as well as any arithmetic expression using it or any other symbol that is meant to be equivalent to a completed infinity, is meaningless.
In other words, the ultimate goal of representing infinity by a sequential progression of transfinite ordinals, that is, the goal of conquering, or circumscribing, the infinite so we can feel that we have a grasp or handle on it, can never be achieved by this means. This is a sign of the connection of infinity to the concept of pattern, by which is meant a finite, and therefore fixed in nature, process that can be repeated as often as we like, i.e., that we can circle or loop back to the beginning of and perform again as often as we like. In the case of the natural numbers in canonical order, this process, this pattern, is known is set theory as the successor function. Once the pattern, or finite, repetitive algorithm, of the successor function is understood, we simultaneously understand that the application of it can never have a definite or complete end. In carrying the operation of successor addition over from the finite numbers to the transfinite numbers, we have really done nothing but continued, in a disguised way, the pattern of the successor operation that was well-defined among the finite numbers, while at the same time believing that we have added nontrivially to the store of knowledge about number and quantity. But if we strip from the operations of transfinite arithmetic the flawed assumption that an infinite sequence can have an end, and any implications of this assumption, and make no other changes to our process, we are left with nothing but the natural numbers themselves, and their arithmetic properties and expressions.
The same can be said for transfinite cardinal numbers. The symbol 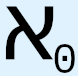 is typically used to represent the cardinality of ω, i.e., the “number of elements” in the set of natural numbers considered as a whole, i.e., as a completed entity. In fact,
is typically used to represent the cardinality of ω, i.e., the “number of elements” in the set of natural numbers considered as a whole, i.e., as a completed entity. In fact, 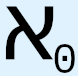 is the cardinal number for every one of the ordinal numbers in the long list of ordinals from two paragraphs ago, which means that every one of these incredibly large transfinite ordinals has, according to this scheme, the same number of elements, and furthermore, these elements are countable, i.e., they all have the same number of elements as the set of natural numbers. This itself is an example of pathological behavior, as defined above. The ordinal ω is then called the initial ordinal of all these other ordinals, because it is the first ordinal in the infinite sequence of transfinite ordinals that all have
is the cardinal number for every one of the ordinal numbers in the long list of ordinals from two paragraphs ago, which means that every one of these incredibly large transfinite ordinals has, according to this scheme, the same number of elements, and furthermore, these elements are countable, i.e., they all have the same number of elements as the set of natural numbers. This itself is an example of pathological behavior, as defined above. The ordinal ω is then called the initial ordinal of all these other ordinals, because it is the first ordinal in the infinite sequence of transfinite ordinals that all have 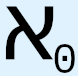 for their cardinality, and as such ω is sometimes called ω0 instead. But this itself is a contradiction, because ω is supposed to be the ending point of the natural numbers, meaning there are no more natural numbers after this point which can be used to index or identify the “place” in the linear sequence of any further ordinals; and yet each of these incredibly large ordinal numbers can, as a set, still be entirely enumerated by the natural numbers, even after all of the natural numbers themselves, the entire set of finite ordinals, have been completely exhausted in a partial enumeration. Then, by defining what are called Hartogs numbers, we can postulate ordinals that are beyond even the infinite sequence of countable ordinals with
for their cardinality, and as such ω is sometimes called ω0 instead. But this itself is a contradiction, because ω is supposed to be the ending point of the natural numbers, meaning there are no more natural numbers after this point which can be used to index or identify the “place” in the linear sequence of any further ordinals; and yet each of these incredibly large ordinal numbers can, as a set, still be entirely enumerated by the natural numbers, even after all of the natural numbers themselves, the entire set of finite ordinals, have been completely exhausted in a partial enumeration. Then, by defining what are called Hartogs numbers, we can postulate ordinals that are beyond even the infinite sequence of countable ordinals with 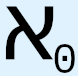 for their cardinality, i.e., ordinals with a cardinality greater than
for their cardinality, i.e., ordinals with a cardinality greater than 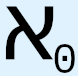 and thus whose set representations have more elements than the total number of natural numbers. But since the cardinality of these sets is greater than
and thus whose set representations have more elements than the total number of natural numbers. But since the cardinality of these sets is greater than 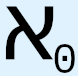 , we must use a different symbol to represent their cardinality. For this, we use
, we must use a different symbol to represent their cardinality. For this, we use 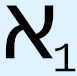 , which is known as the first uncountable cardinal, and the corresponding initial ordinal is called ω1. We will come back to the difference between countable and uncountable, and why, in fact, there is no such distinction, during subsequent discussion of certain topics, including the important topics of the real number line and Cantor’s diagonal argument. But for now, we may notice that with these definitions and symbol manipulations we have started yet another pattern, this time in the sequence of uncountable cardinalities and initial ordinals. As such, it can be expected that it will be possible to find a way to show that this sequence also can never end, which is what has been done in set theory: based on the definitions of Hartogs number and initial ordinal, as well as, crucially, on the extension of these definitions into the uncountable using the logically flawed concept of transfinite recursion37 (see below), we may conclude that “the Hartogs number of [a set] A exists for all A.”38 In other words, not only can we define ω1 as the first uncountable ordinal, but we can also now define ω2, ω3, ω4, … ωω, … – that is, an infinite, i.e., unending, sequence of initial ordinals, each with a higher cardinality than the previous one. This also means that we may define an infinite sequence of uncountable cardinals, each with a “greater” level of uncountability than the preceding one. But it doesn’t end there. We can then define what is called a limit ordinal, in which we envision that this infinite sequence of ever-increasing uncountable ordinals approaches a limiting point, in the manner of a limit in calculus, where the infinite sequence finally, at “infinity,” converges to the limit ordinal that has an infinitely higher uncountable cardinality than any of the initial ordinals in the infinite sequence that led up to it. But even this does not end the sequence. At greater levels still, there are such concepts as strong limit cardinal, inaccessible and strongly inaccessible cardinal, and various other types of so-called “large cardinals.”
, which is known as the first uncountable cardinal, and the corresponding initial ordinal is called ω1. We will come back to the difference between countable and uncountable, and why, in fact, there is no such distinction, during subsequent discussion of certain topics, including the important topics of the real number line and Cantor’s diagonal argument. But for now, we may notice that with these definitions and symbol manipulations we have started yet another pattern, this time in the sequence of uncountable cardinalities and initial ordinals. As such, it can be expected that it will be possible to find a way to show that this sequence also can never end, which is what has been done in set theory: based on the definitions of Hartogs number and initial ordinal, as well as, crucially, on the extension of these definitions into the uncountable using the logically flawed concept of transfinite recursion37 (see below), we may conclude that “the Hartogs number of [a set] A exists for all A.”38 In other words, not only can we define ω1 as the first uncountable ordinal, but we can also now define ω2, ω3, ω4, … ωω, … – that is, an infinite, i.e., unending, sequence of initial ordinals, each with a higher cardinality than the previous one. This also means that we may define an infinite sequence of uncountable cardinals, each with a “greater” level of uncountability than the preceding one. But it doesn’t end there. We can then define what is called a limit ordinal, in which we envision that this infinite sequence of ever-increasing uncountable ordinals approaches a limiting point, in the manner of a limit in calculus, where the infinite sequence finally, at “infinity,” converges to the limit ordinal that has an infinitely higher uncountable cardinality than any of the initial ordinals in the infinite sequence that led up to it. But even this does not end the sequence. At greater levels still, there are such concepts as strong limit cardinal, inaccessible and strongly inaccessible cardinal, and various other types of so-called “large cardinals.”
Notice that no matter where we stop, no matter how “large” we make our next uncountable cardinal (or ordinal), our implicit assumption is that even though the symbol for the transfinite number represents an infinite quantity, we are still justified in treating it as a finite, fixed, unitary, circumscribed, completed, mathematically manipulable object. And from such treatment it can be immediately perceived that there could be something still larger. This is a one-track kind of mindset, and it is a mindset that is (ironically) limiting, because in thinking that we can come to an understanding of the ultimate nature of infinity by continuing this process of finitizing the infinite, we make it that much harder to recognize and acknowledge in a nontrivial way the logical flaw on which this entire progression is based. In a complex set of interconnected ideas, such as that embodied by set theory and its interconnections with other branches of mathematics, many ideas are likely to be valid and based on sound assumptions and axioms, and in the case of infinity and how the concept is treated in set theory, not all is unsound. However, as we have been discussing, certain key parts of it are unsound, and have been from the moment the idea of the transfinite was introduced by Cantor. It has been said that in continuing the path of searching for ever “higher” levels of infinity, we are operating in the context of a “hierarchy postulating the existence of larger and larger cardinals” which provide “better and better approximations to the ultimate truth about the universe of sets,” and that ZFC is “just one of the stages”39 of this hierarchy. It is not impossible that one of the results of this effort will be a legitimately clearer understanding of the nature of sets and the nature of infinity. But in order for a clearer understanding to actually result from this effort, one of the steps along the way must be the recognition of the logical error of treating infinite quantities as if they were finite. The use of large cardinal axioms, ordinal arithmetic, cardinal arithmetic, and related concepts, in the context of a broader set of logically valid ideas, to uncover the truth about and connections between various mathematical concepts and constructs, may help mathematical investigative work in certain ways, but the more we rely on such flawed concepts, i.e., the deeper we dig ourselves in, the further we remove ourselves from the reality we are trying to describe and understand, and the more the mathematical symbols we manipulate become nothing more than symbols.
Before moving to the next topic, let us briefly discuss transfinite induction and transfinite recursion. Mathematical induction is a method of proof for items that can be placed in a sequence patterned in some way by the natural numbers, whereby we first prove that a statement about the first item in the sequence is true, then prove that if the statement is true about the nth item it must also be true about the (n+1)th item, and from these two results we conclude that the statement is true about all items in the sequence. On the other hand, recursion is the process of performing an operation on an initial input and then taking the output of this operation and making it the next input to the same operation; each time the operation (or function) takes an input, an index sequence is increased by one to keep track of the number of times this single operation has been applied. Now, both operations, induction and recursion, are well-defined when the nth item in their respective sequences is a finite number, i.e., a natural number. But it should be plain from the above discussion regarding the transfinite that when we try to take, for example, the ωth item, or operation, in the sequence, or the (ω+1)th item or operation, etc., we are not doing or saying anything meaningful. The only reason that the process of “extending” the operations of induction and recursion into the transfinite seems meaningful is that we have already accepted the dubious validity of the finitizing of the infinite that began when we assumed that there could be an end to the infinite sequence of natural numbers, and that the “number” just beyond this point could be represented by a finite symbol that can be manipulated meaningfully by arithmetic operations. Once we have done this, it is no great leap to the idea that it is valid also to extend the operations of induction and recursion into the transfinite. But as we have seen, the entire concept of such an extension is based on a logical error, and is thus fundamentally flawed. We may be able to deduce “interesting” mathematical results on the basis of the assumption that there is no logical error in finitizing the infinite, and, in fact, this is what has happened in set theory, with such results forming a significant part of set theory. But these results do not, and cannot, apply to reality, precisely because they are based on a logically flawed assumption, while reality is, and always must be, logically self-consistent.
As in the previous section, we will see here that the, typically subconscious, foundational assumptions that have made CH such an intractable problem are based partly on logical flaws and partly on imprecision in the definition of terms. We will begin our discussion with the topic of the real numbers and the real number line.
Real numbers are envisioned as being points on a straight line in order, from left to right, of increasing magnitude, such that every possible magnitude or fraction of a magnitude is represented by a point on this line, i.e., by a real number. A point on this line, i.e., the position of a single real number on this line, is approximated by a single dot that may be made by the tip of a pencil, though an actual point on the real number line is solely a position and has no breadth, width, or length, unlike a point that may be made by the tip of a pencil. As such, a point on the real number line cannot be said to exist in the physical sense. However, even in the conceptual arena in which a point on the real line is understood to be nothing more than a position, at a certain important level it cannot be said to exist in this sense either, and this is the beginning of a clarified understanding. Start by imagining the closed unit interval [0, 1]. If we arbitrarily assign each unit interval on the real number line the Euclidean distance of 1 in., then we may say that this unit interval has a 1 in. magnitude (i.e., length) in Euclidean space (or, equivalently, that its Lebesgue measure40 is 1 in.). If we divide this unit interval into two parts by a perpendicular line at a fixed point, and then take one of these two parts and divide it, and keep this process going, after a certain number of divisions the practical tools that we may be using to make these divisions (if we are using tools of some kind to actually divide a line that we have drawn) will reach the limits of their applicability and will no longer allow us to make further divisions; but conceptually we may imagine ever-increasing degrees of magnification on smaller and smaller stretches of the real line so that we can keep making these divisions for as long as we like. Imagine that after each division, the length of the stretch of line that we choose for our subsequent division is less than half the length of the the line segment we just divided. This process, as stated, can never end, precisely because there is no non-zero component of length that is the smallest possible length that one can reach; and the reason for this is that the definition of length implicitly includes the concept of infinity, such that, as with the natural numbers and their infinite increase, no matter how many times we choose to divide the real line, we will always be able to divide it further using the same pattern, the same function, operation, process, etc., as we have been using. Another way of stating this is that because every position at which we divide the real line is a position only and has no extension, however small, in any direction, a linear accumulation of such points, no matter how many of them we accumulate, will never become even the tiniest fraction of a non-zero length accumulation, i.e., of a line or line segment. We may imagine accumulating an infinite number of these points (which, as discussed above, can never actually be done since “infinite” means “without end” or “without bound”) and trying to place them next to each other to create a line, but even “after” such an infinite accumulation, there will still be literally nothing, since a point, which is of zero extent in any spatial direction, cannot add any length to anything, and in particular cannot add any length to another point. But then, there is still the seemingly intuitively valid idea that if enough real numbers are accumulated linearly they will create a non-zero, positive Euclidean length measure, so that, for example, if we draw a straight line that is supposed to be a continuous linear accumulation of real number points of 1 inch in length on a piece of paper, it can be measured against a ruler and found to be precisely 1 in. There is something incongruous about this.
The problem of understanding the continuum, i.e., the set of real numbers, typically thought of as being arranged in continuous linear fashion, has been a celebrated problem in set theory and analysis for over a century, beyond just the CH question. This in itself indicates just how difficult it is to pin down precisely what we mean by the real numbers and the real number line. There have been numerous definitions of real numbers, such as the familiar decimal representation, that based on Cauchy sequences, that based on the concept of a Dedekind cut, or the concept of a complete ordered field. Each of these definitions attempts to come to terms with the fact that though we envision the reals as being placed next to each other to make up a line (of infinite length), each number itself is only a position on that line and has no length of its own with which to extend the line. Nonetheless, each fixed, unchanging “point” on the line is defined by a single real number, and the real number is thought of as being synonymous with that fixed point, i.e., with a fixed and unique quantity or magnitude if we have imposed a Euclidean distance metric onto the line. In the case of a number whose decimal representation is finite, it is easy to see, in finite terms, how this number fits on the real line – for example, the fraction ½ has a decimal representation of 0.5, and it is no difficult task to see how this value of 0.5, as a finished, fixed quantity, can be marked on the real number line. But what about the fraction ⅓? This is, of course, a rational number, since it is a ratio of integers. But its decimal expansion, though it does repeat, never ends: 0.33333… . Is there any significance to this difference between these two rational numbers? In fact, there is. It is that the position on the real line of the number ⅓ when this number is represented by its decimal expansion cannot be determined in a finite way. Certain definitions of the reals express this by using the concept of a limit to define such real numbers, though this is typically done only for the irrational numbers, i.e., numbers whose decimal representations neither repeat nor terminate and thus which cannot be written as ratios of integers. And this is the key difference. The decimal expansions which are finite, i.e., terminating, are equivalent to numbers, i.e., finite, fixed quantities on the real number line; however, the decimal expansions which are not finite are not equivalent to numbers, because they are themselves not fixed points on the line; rather, each is an always-moving sequence of points that gets closer and closer to a fixed limit point as more and more numbers are added to the end of its decimal expansion, with the decimal expansion never actually reaching the fixed limit point. In fact, it is the limit point itself that is the number, not the decimal expansion, which can only ever be an approximation of the number. Here we must recall the definition of infinity given above, viz., the quality of increasing without bound. A number is a definite point on the real number line; that is, it is finite. A non-terminating decimal expansion is, as its name states, non-terminating, and thus contains within it an infinite sequence of numbers, and with each number added to the end of this sequence the approximation to the limit point being approached by this sequence changes position on the real line. The essential conclusion here is that because the sequence is infinite, it never stops changing position on the real line – no matter how many digits are added to the end of the expanding decimal sequence, an infinite number of digits can be added beyond them. In other words, if a number is defined to be a fixed point on the real number line (and it makes no sense to say that a number on the line is anything other than a fixed point), then since an infinite decimal expansion that leads up to, but never reaches, such a fixed point is itself not a fixed point on the real line and never can be, it is not appropriate to call such a sequence a number at all. In other words, finite, fixed quantities such as 300, -186.8979, -19, 0.33, 1, 1.5, 2, 2.4, 2.9, 3, 3.141, 4, 5.099, etc., on the one hand, and infinite decimal expansions, such as -9.44444…, 0.33323332…, 0.25252525…, 2.71828182845904…, 3.141592653…, on the other, are not the same type of mathematical object. To be clear, the limiting values of the in-finite decimal expansions are themselves finite quantities, since it is a well-defined conception that does not run afoul of logical errors to conclude that each of these limiting values has a single, fixed position on an imaginary straight line that has an arbitrarily marked reference point, and as such it is appropriate to call the limiting values numbers. But it must be emphasized that the infinite decimal expansions themselves are not equivalent to the limiting values, and never can be, because, as stated, infinity means to never end, and thus the decimal expansions themselves can never reach the limiting values.
But this analysis is missing something. If, as stated above, no amount of points could ever produce any length beyond zero, then how is it possible to say that there could be a continuous, i.e., without gaps, linear sequence of these points such that we can mark off varying positions of Euclidean distance on this linear sequence that correspond to different lengths or numbers? And here we get to the crux of the matter. There is a psychological conflation of these two concepts, the concept of Euclidean distance and the concept of an infinite linear sequence of points of zero length that can somehow create positive length in their linear aggregate and can thus be made to correspond to the familiar notion of Euclidean distance. But the reality is that, as stated above, no amount of points of zero length could ever be made to aggregate linearly to anything more than zero length. It is a logical error to believe otherwise. In our conflation of these two concepts in, e.g., calculus and differential equations, or even in basic algebra when, e.g., we are graphing a polynomial in the Cartesian plane, we are able to gloss over and effectively ignore this logical error, and thus treat these two concepts as equivalent, because these branches of mathematics do not need to be precise enough for this logical error to become relevant; they can, in other words, do all that they need to do based on the high degree of similarity in certain relevant respects between the concepts of linear Euclidean distance and continuous geometric lines, on the one hand, and the, as we must emphasize, logically imprecise, concept of the “real number line,” on the other, without having to take account of the fact that at their core these two things are not equivalent, and never can be. We may say, for example, that the irrational number π is clearly defined as the ratio of the circumference of a circle to its diameter. So how is this not a number? But this question confuses a fixed Euclidean length or distance with an infinite, ever-changing sequence of numbers. The ratio itself is finite and fixed, and thus equates to a single well-defined magnitude, but the decimal representation of this number will never end, i.e., it will never reach the equivalent of the magnitude of the ratio’s Euclidean distance. We believe we are using the symbol π to represent one thing, but this finite symbol really represents two distinct things, a finite, and thus fixed, Euclidean distance and an infinite sequence of digits, that have been conflated and are treated as if they were the same thing. These two things are similar enough out to the appropriate finite number of decimal places that we can make accurate approximate calculations based on the formula C=πd with our scientific tools, and thus similar enough that we can simply gloss over the fact that one of the things that the π symbol in the formula C=πd represents is an infinite, and thus always changing, sequence of digits. Therefore, we can also gloss over the fact that it make no logical sense to try to multiply this infinite sequence with the fixed, finite diameter of a circle in order to obtain the circle’s fixed, finite circumference, since for the concept “multiply” to have any meaning the numbers being multiplied must both be fixed quantities, i.e., they must be represented numerically in their finite form, if they have one – in the case of rationals, as fractions, or alternatively as decimals if their decimal expansions terminate.41 This goes for the values of C and d as well – if these are non-terminating in their decimal expansions, then when we make concrete calculations with them, at most we will only be able to calculate using finite approximations of these numbers, not the numbers themselves, except in the case of such numbers as can be exactly represented in numerical form as ratios of integers. And yet, as we have said, the limit points of such non-terminating decimal sequences are finite, being fixed positions on a geometric line, and these limit points represent, from a 0 reference point, the exact values of the fixed magnitudes, whether the numbers are rational or irrational. This precise distinction is not relevant for much mathematical work, but for CH it is essential.
The foregoing is the most counterintuitive statement in this entire paper. We are so used to equating the infinite decimal expansion, which when thought about or written is necessarily finite, typically with an ellipsis at the end which is intended to mean “all the rest of this infinite sequence of numbers,” with the fixed, finite limiting value that our approximate, ellipsized version of the infinite decimal expansion is supposed to represent. But there is a fundamental difference between these two things, the one having an essentially infinite character, the other having an essentially finite character. In fact, the fact that we are already comfortable with such equating in the realm of individual numbers with finite magnitudes makes it that much easier to ignore the logical error in treating the natural numbers in their totality as a finite thing, and makes it that much easier to accept other logically flawed ideas and conceptions beyond this, such as the idea that there could be such a thing as a “limit ordinal,” or that there could be numbers even beyond this. It is important to note again that the concept of a limit itself is not being challenged, and, as we understand from calculus, analysis, differential equations, etc., the concept of a limit is useful in a wide variety of circumstances, and produces correct results. The point here is not to challenge any of these results, but rather to spotlight an essential misconception in certain of our foundational ideas that, while irrelevant to many mathematical pursuits, is nonetheless highly relevant to others, and, in particular, to CH. The logical error which causes the misconception that an infinity, such as the natural numbers, can be treated as if it were a completed entity and manipulated in various ways as such, is the same logical error that leads us to believe that an infinite decimal expansion can be treated as if it were a finite number, rather than as what it is, viz., an infinite sequence of smaller and smaller magnitudes which approaches a finite number, but which never actually reaches it. We may say then that the practical conceptual tool in mathematics of treating an infinity as a finite thing, such as we do in, e.g., integration and differentiation in calculus, has certain bounds of applicability, and within these bounds this equating of an infinity with a finite thing does not interfere with the soundness of our results because our results do not in any way directly or essentially rely upon or make reference to the logical error inherent in such equating, so that this equating is used in such cases solely as a convenience to make mathematical work easier. Another way of saying this is that the process of taking a limit42 involves a smoothing over and ignoring of the logical error of equating an infinity with a finite thing, and that this is acceptable in many circumstances because the practical results of such an operation with regard to things in the real world that we might wish to measure are seen to accord as accurately as we like, subject to the limitations of our scientific tools, to the process of successive finer and finer approximations to a limiting value as expressed formally in the mathematical concept of a limit, and also because a limit itself is nothing but an expression of a pattern that has been found in an infinite sequence. In other words, we do not need to take the actual limit (which is impossible) in the real world which we are measuring and trying to understand, but are able to feel satisfied with a finite, though perhaps highly accurate, approximation, or with the fact that we can see a pattern in the infinite sequence, which then allows us to see whether the sequence approaches a finite number or not, and in the former case to know the finite number which the sequence ever more closely approaches. We then see this high degree of accord between the practical measurements and the idealized mathematical expectations, and, given that such accord is the primary goal in our mathematical pursuits (i.e., in the practice of mathematics we seek, either directly or indirectly, to describe and explain the real world’s essential logical makeup and the behavior of matter within this context), we simply do not think further, or at all, about the essential flaw in equating an infinity with a finite thing, since such considerations in this conceptual and practical context are irrelevant. But because, for powerful emotional reasons, we desire absolute certainty to the extent we can possibly obtain it, we then go back to the underlying mathematics and define things even more precisely with concepts like Dedekind cuts and Cauchy sequences, and this added “precision” makes us feel that much more confident that our equating of infinities with finite things is justified, which then makes it easier in our investigations in other areas to ignore or downplay the significance of this problem.
But any logical error in our premises will eventually show itself, often well before we recognize it for what it is. When statements, such as CH, are made that directly relate to or essentially depend upon the logical error, and whose meaning and significance and nature can only be understood after recognizing the logical error for what it is, i.e., whose solution cannot be obtained by a “reasonable approximation” that glosses over the logical error, then we have a different sort of beast, and then our investigations in the context of the systems of mathematical thought that produced such statements and that are themselves partly based on this logical error must be understood as being partly based on a logical error, so that we may come to step outside these systems and learn to see things from an unconventional, and more accurate, angle.
We will next briefly discuss the concept of measure. The concept of measure in mathematics is a generalization of the familiar concepts of length, area, and volume to n dimensions (as well as of other things, such as “magnitude, mass, and probability of events,”43 etc., which we will not discuss here). As such, it attempts to extract and preserve the essential properties across all these familiar concepts and express them in the language of set theory, e.g., the measure of the sum (union) of two sets must be equal to the sum of the measures of the individual sets, or the measure of the empty set (i.e., {}) must be 0, or the measure of a smaller set must be smaller than the measure of a larger set. In a particular formulation used in set theory which has relevance for CH, the measure of a single-element set is defined to be 0, and the measure of a countably infinite union of sets (i.e., a union of sets whose total number equals that of the natural numbers) is the sum of the individual measures of each of the sets.44 “A consequence of [these two parts of this definition of measure] is that every at most countable [i.e., finite or countable in number of elements] [set] has measure 0. Hence, if there is a measure on [a set], then [the set] is uncountable. It is clear that whether there exists a measure on [a set] depends only on the cardinality of [the set]… .”45 We should note also that a key part of the definition of measure for a set is the maximum value that a measure can be. For convenience, Hrbacek, in their definition, make the maximum possible measure of a set, whether finite or infinite, equal to 1, though, as they say, this is only a convention: other measures, such as the “counting measure,” would have an infinite set have a measure of.46 Further, Hrbacek mention the open question “whether the Lebesgue measure47 can be extended to all sets of reals,” relating this to what they call the measure problem, a technical question regarding the definition of measure given, and then go on to say, “The measure problem, a natural question arising in abstract real analysis, is deeply related to the continuum problem, and surprisingly also to the subject we touched upon [earlier] – inaccessible cardinals. This problem has become the starting point for investigation of large cardinals, a theory that we will explore further in the next section.”48 This definition of measure and the subsequent comments show key signs of the essential logical error underlying modern set theory’s investigation of infinity, in that (a) the definition has been made in such a way as to reflect the underlying feeling that, somehow, it just feels right to make all at most countable sets have measure 0, while any measure above 0 must correspond to an uncountable set, and (b) the comments that Hrbacek make have shown that this area of investigation, i.e., that of understanding the relationship between the familiar concept of Euclidean length or distance, on the one hand, and the set of points that make up the real line, on the other, is particularly thorny in set theory and analysis; in fact, it is foundational.
But let us recall the discussion above regarding stringing together an infinite number of points of zero length. We concluded that, as makes logical sense, no line, or even the tiniest part of a line, could ever be created in this way, much less a line of infinite extent as the real line is imagined to be. How, then, would it ever be possible to find a way to reconcile the concept of a linear sequence of points with a non-zero, positive measure of Euclidean length? In fact, these two things cannot be reconciled, because they are incommensurable – they are two fundamentally different types of thing, and there is no way to bridge the gap between them at a foundational level. We may bridge this gap at an approximational level; not at a foundational one. Euclidean distance of any positive measure, no matter how small, can never be equated to a linear sequence of points of zero length that have no gaps between them, since the latter will always remain zero, i.e., 0 + 0 + 0 + 0 + … will always be zero, no matter how many 0s are added to this sum. This irreconcilability is implicitly recognized in the defining of the measure of any at most countable set to be 0. But then the definition and concept of measure take things too far and plant their flag on the same fundamental logical error that we have been discussing, i.e., they assume that it is possible to somehow go beyond this in terms of length by simply adding more points “after” a countable number of points have been added to the linear sequence. The measure of such a post-countable number of point strung together linearly is now defined to be greater than 0. After all, this makes sense, doesn’t it? If a countably infinite set has a measure of 0, and if uncountable infinity is, in some way, fundamentally above or beyond countable infinity, then its measure should be considered to be fundamentally above or beyond the measure of countable infinity. The only problem with this is that the first sequence, the countably infinite sequence, is infinite, and as such it can never end; therefore, it is impossible to add points to a linear sequence that are beyond the points in the countably infinite sequence. This is not even to mention the fact that in adding points to the linear sequence beyond the countably infinite sequence of points, we are adding, well, points to the linear sequence, i.e., entities of zero length, and so adding such points still will not be able to increase the length of the line beyond 0. Therefore, under the assumption that uncountable infinity exists it is more correct to say that both countable and uncountable infinity have measure 0. If one objects by saying that in adding points “beyond” the end of the natural numbers in the way just described we are adding them in a “countable way,” and so of course the measure never rises above zero by doing this, then one has stumbled upon the main point of this paper, which is that the only possible way to add points, or to add numbers or elements to a set, is to do so countably, because the concept of uncountable infinity is logically meaningless.
It is significant that the idea that uncountable infinity has a non-zero, positive measure is part of the definition of measure that Hrbacek provide, and not a logical conclusion based on the actual measuring of an uncountable set or a direct argument about uncountable sets and their measures. Recall that the definition of measure states explicitly that any at most countable set has measure 0. The implication, as Hrbacek state, is that if a set has a non-zero, positive measure it must be an uncountable set. But this does nothing to guarantee that uncountable sets exist; the implication assumes that there is a difference between countable and uncountable infinity, and, in particular, that the reals are uncountable as a result of the diagonal argument and therefore serve as a concrete example of an uncountable set, and as such assumes that comments about sets with non-zero, positive measures in the context of this definition of measure are about sets that can actually exist. If there is no difference between countable and uncountable infinity, if, in fact, this difference is nothing but a pathological result that is an outgrowth of a logical error at the foundation of set theory, then in the context of this definition of measure it is a logical error to say that any set, however large, can have a measure greater than 0. In fact, from the preceding discussion it should now be clear that this is the case, because the level of so-called “uncountable” infinity can never be reached, since the “highest point” of countable infinity can never be reached. But we will come back to this point in the next section when we directly examine Cantor’s diagonal argument, the argument that in the late 1800s essentially started the theory of multiple levels of infinity by seeming to prove about infinity something substantial, profound, and highly unexpected, and by means of a simple argument to boot – i.e., by being what in the mathematical world would be called an elegant, beautiful, or powerful result. We will pinpoint the essential flaw in the diagonal argument, and will thus show why it, too, is founded on the same logical error as everything else we have so far discussed.
Before turning to a discussion of the power set operation, one further thing should be noted. The quotes above from Hrbacek indicate the importance to the mathematical mind and to mathematical practice of finding an ideal or perfect analytical representation of Euclidean distance, since distance is a common and essential aspect of our understanding of, and our navigation within, the world around us, and, after all, the usefulness of mathematics, both to mathematicians and non-mathematicians, ultimately depends on its utility in helping us understand and navigate the world. It is also true that the real number line is a well-tried, ubiquitous, foundational, and deeply revered concept in mathematics. It is a typical mode of thought in the human psyche to seek similarities between things, especially things that are significant or important to us; this allows us to locate patterns in the world, and thus to be able to use these patterns to find better ways to navigate the world, achieve our goals, avoid danger, and find happiness. But in this quest to find patterns, which is often overlain by high emotional stakes, it is sometimes, or even often, the case that we see two things that appear to be similar, but in actuality are fundamentally different. However, due to the often significant need to find patterns, we may conflate such superficially similar things in our minds and our concepts and treat them as the same thing, or essentially the same thing, especially if the two things are similar to each other in ways we can notice and which are relevant to us, and if their differences, at least for a time, perhaps a long time, never show themselves in ways that affect the practical benefits we derive from such a conflation. But if we choose to dig deeply enough, we will eventually find that the two things are, in fact, fundamentally different in one or more ways, and that we had simply not noticed these fundamental differences until it became absolutely necessary, for one or another of our practical purposes, to do so; and we will start to realize that we had seen signs of these essential differences early on but had not, at the time, understood their true significance.49 Such superficial conflation which glosses over a fundamental distinction is the case with the conflation in mathematics of the concept of Euclidean distance and the concept of the real number line. Such a conflation is highly useful within the bounds of its applicability, but once these bounds are breached, we start to see pathological behavior and impossible mathematical results. It is at such breach points that the usefulness of this conflation, this practical conceptual tool, begins to break down, and if our mathematical investigation beyond such points continues assuming the validity of the conflation, flaws, errors, and contradictions will persist in our results, i.e., flawed results will persist until we make the necessary conceptual correction.
In the final topic of this section, we now turn to a brief discussion of the power set operation in set theory. The power set operation is simply the operation that creates a set out of all the subsets of a given set. If the set is called S, then the power set operation can be written as P(S) (though, as we saw earlier in the discussion of Feferman’s ideas, different authors may use different symbols to represent this operation). For example, if S = {a, b, c}, then P(S) = {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}, where ∅ is the empty set, i.e., the set with no element (also written as {}), and the set S itself is also considered a subset of S. Note that the number of elements in the power set of S is 8, and the number of elements in S is 3. We can see that there is a relationship here, in that 23 = 8. In fact, this is the case for every power set, i.e., if S contains n elements, then the number of elements in the power set of S is 2n. However, what if S = ℕ? In fact, given the preceding discussion, we can say right away that it is logically impossible to take the complete power set of S in this case, because the number of elements in ℕ is infinite; also, it does not make mathematical sense to raise 2 to the power of infinity. There will be objections to this statement, because it is a very common thing in set theory to do precisely this, and set theorists are very familiar with the concept of raising a number, finite or infinite, to an infinite power. However, familiarity does not mean correctness. In fact, the taking of a power of a number crucially depends on the exponent being a fixed, i.e., unchanging, and therefore finite, quantity. But in the case of the magnitude of the set of natural numbers, this quantity is not fixed, unchanging, or finite, and never can be, and so in fact there is no such magnitude, because for the concept of “magnitude” to be meaningful in the first place the magnitude in question must be fixed. To repeat, the “set” of natural numbers does not have a magnitude. The use of the finite symbol ω or the finite symbol 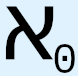 to represent this infinite quantity does nothing to resolve this issue, but rather unceremoniously glosses over it instead. The concept of the magnitude, or “cardinality,” of ℕ is, in fact, not meaningful, because an essential part of the definition of ℕ is that its membership increases without bound, i.e., an essential part of the definition of ℕ is the concept of infinity, and therefore as we keep adding elements to the set without bound its magnitude will be always changing. This must be the case, because if we stop at any point in order to stop the set’s magnitude from changing, then the set which results is only a finite set, meaning that it does not include all the natural numbers and therefore is not equal to ℕ.
to represent this infinite quantity does nothing to resolve this issue, but rather unceremoniously glosses over it instead. The concept of the magnitude, or “cardinality,” of ℕ is, in fact, not meaningful, because an essential part of the definition of ℕ is that its membership increases without bound, i.e., an essential part of the definition of ℕ is the concept of infinity, and therefore as we keep adding elements to the set without bound its magnitude will be always changing. This must be the case, because if we stop at any point in order to stop the set’s magnitude from changing, then the set which results is only a finite set, meaning that it does not include all the natural numbers and therefore is not equal to ℕ.
But then let us take a moment to analyze, in light of the above ideas, the key expressions involved in CH and generalized CH. If we recall, CH states the following:
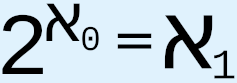
That is, the number 2 raised to the infinite power of the “number” of natural numbers50 is equal in magnitude to the first uncountable cardinal number. Recall, further, that generalized CH states the following:
For every infinite cardinal in the sequence of infinite cardinals, CH holds; that is,
for all ordinals α, starting at α=0.
The problem since 1878 has been that, despite the seeming precision with which CH is stated, no one (let’s be honest with ourselves) has been able to get a handle on what, precisely, CH seems to be saying. It is not the same with other mathematical problems, such as, e.g., Goldbach’s conjecture, which simply states that every even natural number greater than 2 is the sum of two primes. This statement is clear and unambiguous, i.e., we have a clear understanding of what it says, regardless of whether it will ever be proven. CH and generalized CH do not give us the same kind of unambiguous clarity.
But it is now possible to see why this is so. First, the concept of a fixed infinite quantity, such as 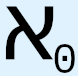 , is logically meaningless, because fixed means finite, finite is the opposite of infinite, and therefore it not meaningful to say that something can be both infinite and finite at the same time, i.e., that something can both increase without bound and not increase without bound at the same time. Since, then, the concept of
, is logically meaningless, because fixed means finite, finite is the opposite of infinite, and therefore it not meaningful to say that something can be both infinite and finite at the same time, i.e., that something can both increase without bound and not increase without bound at the same time. Since, then, the concept of 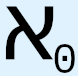 is not logically meaningful, it is also not logically meaningful to treat
is not logically meaningful, it is also not logically meaningful to treat 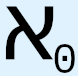 as if it were a number and proceed to raise 2 to the
as if it were a number and proceed to raise 2 to the 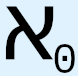 power. Further, since
power. Further, since 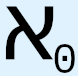 is itself supposed to be an “infinite” quantity or magnitude, it is not logically meaningful to raise 2 to the
is itself supposed to be an “infinite” quantity or magnitude, it is not logically meaningful to raise 2 to the 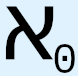 power for another reason, namely that the operation of raising a finite number to a power is itself only logically meaningful if the number that is used as the exponent is unchanging, which means that the exponent must be finite; an infinite quantity, such as
power for another reason, namely that the operation of raising a finite number to a power is itself only logically meaningful if the number that is used as the exponent is unchanging, which means that the exponent must be finite; an infinite quantity, such as 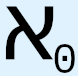 , on the other hand, has within it, as part of its inherent nature, that it never stops changing. Additionally, the concept of
, on the other hand, has within it, as part of its inherent nature, that it never stops changing. Additionally, the concept of 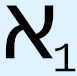 has no logical meaning, first because, like
has no logical meaning, first because, like 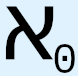 , it is a symbol which is treated as a fixed, bounded, unchanging, finite thing that is manipulable in set-theoretic operations as one would manipulate any actually finite thing, even though inherent in the meaning of the symbol
, it is a symbol which is treated as a fixed, bounded, unchanging, finite thing that is manipulable in set-theoretic operations as one would manipulate any actually finite thing, even though inherent in the meaning of the symbol 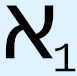 is the concept of infinity, and this conflation of the finite with the infinite is a logical contradiction; and second, because
is the concept of infinity, and this conflation of the finite with the infinite is a logical contradiction; and second, because 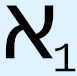 is supposed to represent “uncountable” infinity, which we are told is an inherently or fundamentally different “kind” or “level” of infinity than countable infinity, and this also is a logical contradiction, i.e., a logical error, because there is no such thing as more than one level of infinity – as we have discussed, “countable” infinity is all there is, because “countable” is equivalent to the “cardinality” of the natural numbers, and the natural numbers never end, so it is impossible to add any points to a linear sequence of points, or any numbers to a sequence of numbers, beyond the “end” of the natural numbers. The belief that it is possible to do this is nothing more than wishful thinking in the guise of rigorous mathematical formalism. Also, these same conclusions apply equally to the
is supposed to represent “uncountable” infinity, which we are told is an inherently or fundamentally different “kind” or “level” of infinity than countable infinity, and this also is a logical contradiction, i.e., a logical error, because there is no such thing as more than one level of infinity – as we have discussed, “countable” infinity is all there is, because “countable” is equivalent to the “cardinality” of the natural numbers, and the natural numbers never end, so it is impossible to add any points to a linear sequence of points, or any numbers to a sequence of numbers, beyond the “end” of the natural numbers. The belief that it is possible to do this is nothing more than wishful thinking in the guise of rigorous mathematical formalism. Also, these same conclusions apply equally to the 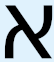 symbols in generalized CH. Finally, since the two sides of the equation in the statements of CH and generalized CH are both logically meaningless, it is also logically meaningless to attempt to equate them, since equating two numbers implies the ability to unambiguously know their magnitudes so that it can be determined whether or not they are equal. Since neither side has an unambiguously determinable magnitude, it is impossible to know the magnitudes of the two sides of the equations in order to compare them.
symbols in generalized CH. Finally, since the two sides of the equation in the statements of CH and generalized CH are both logically meaningless, it is also logically meaningless to attempt to equate them, since equating two numbers implies the ability to unambiguously know their magnitudes so that it can be determined whether or not they are equal. Since neither side has an unambiguously determinable magnitude, it is impossible to know the magnitudes of the two sides of the equations in order to compare them.
The result, then, is clear: CH and generalized CH are meaningless statements, because they are based on logically flawed assumptions, concepts, and definitions. In other words, it is impossible to assign a definite truth value to these statements, since assigning a truth value to a statement presupposes that the statement is based on clear and logically valid assumptions, concepts, and definitions. This is the source of the vagueness that Feferman noticed and sought to explain. In his earlier paper, Feferman commented that the operation of the power set of ω is “clear enough,” but that the further operation of the power set of the power set of ω is not clear, and that “the meaning of CH depends essentially on quantifying over all such subsets.”51 Here Feferman is essentially correct: CH states that the magnitude of the power set of a set of infinite magnitude is equal to the magnitude of the next higher “level” of infinity; the power set of ω is the set of all subsets of the natural numbers, and CH postulates the magnitude of this power set to be equal to the magnitude of the first uncountable level of infinity; but what does it mean to quantify over an uncountable quantity? And yet, if we wish to understand CH, we must be able to understand all its component parts, and this includes having an intuitive understanding of what it means to quantify over an uncountable set. Or even not considering the difference between uncountable and countable, what does it mean to have a set that has a number of elements that equals 2 raised to an infinite power? Additionally, generalized CH states that the magnitude of the power set of the power set of ω is equal to the magnitude of the second “level” of uncountable infinity, and so on. Again, what does it mean to take the power set of a set whose number of elements is the cardinality of the first level of uncountable infinity? In fact, as we have shown, such things are impossible, because they are all based on logically flawed assumptions and definitions, and therefore these statements and operations have no meaning which one might be able to grasp after sufficient thought and reflection; this is the reason Feferman could not make sense of how to quantify over the set of the power set of ω. Another way of looking at this is that since the reals are supposed to be uncountable, this means that they cannot be placed in one-to-one correspondence with the natural numbers; but if, in the process of taking subsets of the reals in order to produce the power set of the reals, we look at each of the subsets produced, we see that it has been produced by selecting, one by one, numbers from the set of reals. But from this it is clear that each real can be made to correspond one-to-one with a natural number, since no matter how many reals we select for a particular subset, and how many subsets we create, we can always match each real, and each subset, to a natural number in an index sequence; and because the natural numbers never end, no matter how many reals we add to each subset or how many subsets we create, we will never reach the “uncountable” realm because we will never exhaust the natural numbers. However, because this makes both the reals and the power set of the reals countable, and the reals, not to mention their power set, are supposed to be uncountable, then it must be wrong to map, as we have done, the reals or the subsets of them to the natural numbers; that is, doing so inevitably leads to the conclusion that these sets are countable. But if we strip from the process of creating the power set of the reals the ability to enumerate the elements pulled from the reals to create the subsets, and the ability to enumerate the subsets, then how could the process of creating the subsets happen at all? In fact, it makes no sense to say that it could. The process of creating subsets of the reals, or simply listing out the reals themselves, entails the ability to enumerate the reals and the subset so created, and it cannot be otherwise. The implicit denial of this fact is a source of the vagueness, the indefiniteness, to which Feferman refers in his discussion of the power set of the reals.
But Feferman does not carry the analysis far enough. He states, in a vague sort of way, that the operation of the power set of ω is “clear enough.” This we may take to mean that it is easy to imagine combining elements of the set of natural numbers into subsets of the natural numbers, and making each such subset an element of a new set called the power set of the natural numbers; and it is easy to imagine this because the natural numbers are countable, and so we have no conceptual qualms with being able to enumerate them, or even – in an imprecise way, because the power set thus created is supposed to be uncountable – to enumerate the subsets of the naturals that we are creating. However, is it not just as easy to imagine taking each of these sets in the power set thus created and combining them as elements of new sets, and adding each of these new sets to a third set that we call the power set of the power set of the natural numbers? At both of these levels of the power set operation we begin with an infinite sequence of concrete, i.e., finite, elements, and we are asked to start making combinations of them into new sets that are then made the individual elements of another set. Therefore, any difficulty we may encounter in conceptualizing the operation of creating subsets at either one of these levels will be equally encountered at the other level, without exception. A key reason why Feferman believes that there is a difference in conceptualizing the power set operation between these two levels, that is, that it is relatively clear how to perform the operation at the lower level but not at the higher level, is that he still holds onto the assumed validity of the idea that there are different levels of infinity, however much he indirectly notices that there just might be something anomalous, something inherently unaccountable, about this notion. Once it is understood that there is no such thing as different “levels” of infinity, the picture begins to clear. But the idea that there are different levels of infinity is a very difficult concept to relinquish, given that a substantial portion of the results in set theory thus far are based on this notion, and given how many years and decades of thought, dedication, and energy have been devoted by many set theorists and philosophers to set-theoretical work under the assumption that there is no logical contradiction in this account of infinity.
The diagonal argument can be made in more than one way. One version of it is as follows. Imagine an infinite list of all the non-terminating decimal sequences in the open interval (0, 1), where each number in the list appears exactly once.52 Also, assume the list is countable. We may use the following as an illustration of part of this list, keeping in mind that it is not necessary for the numbers to be in any particular order:
0.19238242349234…
0.2342389432333…
0.003323423222…
0.99238423234…
0.0000000013323…
0.9999440000001…
0.3333333333333…
0.500000000003…
0.000000000007…
0.77777777777775…
⋮
Now imagine we index these decimal expansions in the order in which they appear from top to bottom, so that the first is indexed to 1, the second to 2, the third to 3, etc.; i.e., we map the natural numbers one-to-one with these decimal expansions in the order in which they appear in the list. Starting with the top element in the list, imagine that we record the number in its first decimal place (in this case, 1), then take the number in the second decimal place of the second element (in this case, 3) and record it to the right of the 1 we took from the first element, and continue this sequence ad infinitum – take the third digit from the third element, the fourth from the fourth element, etc. Let us put 0. in front of this sequence and call this new number b. Therefore, b = 0.1333043007… . Now imagine that we change each of the digits in b by adding 1 to it, and let us call the resulting number c; therefore, c = 0.2444154118… . But this new number c is now different from every number in the above infinite list, because it is different from the nth number in the list in decimal position n for all n, and yet clearly the new number c is the non-terminating decimal expansion of a number in the open interval (0, 1). Thus, it is concluded that there is a contradiction in the initial assumption that these decimal numbers can be mapped in a one-to-one correspondence with the natural numbers, and, in particular, that there must be more real numbers than natural numbers, since the sequence of reals from which we took the number b and to which we added the number c was already assumed to be countably infinite, i.e., to be mapped in one-to-one correspondence with the entirety of the natural numbers; and, furthermore, the reals in our argument were entirely contained within a unit interval, so the list of reals in our argument does not even include all the reals in the rest of the real number line. Therefore, even after the natural numbers are entirely exhausted for the purpose of indexing, the reals as a set or list continue growing. The natural numbers are sometimes called the counting numbers, for obvious reasons, and so due to this supposed distinction between the number of natural numbers and the number of reals, it is said that while the natural numbers are countable, the reals must be uncountable.
But we can already see that there are flaws in this argument: the one-to-one correspondence made in the argument between natural numbers and real numbers does not, in fact, consist of a correspondence between numbers and numbers; it consists of a correspondence between numbers and infinite sequences, which, being infinite, are always changing, and thus the diagonal argument runs afoul of the same logical error that makes it seem valid to say that an infinity, such as the sequence of natural numbers, can be fully circumscribed and bounded, and thus made finite. For the infinite sequences in the diagonal argument are treated as finite things, as being particular, fixed numbers on the real number line, and thus as being fixed, unchanging magnitudes that can be uniquely assigned to particular natural numbers in the index sequence. But it is not the case, and never can be the case, that there are such unique assignments for infinite decimal expansions. A number only has meaning as a fixed, unchanging quantity – if it was not fixed and unchanging, then every time it changed it would change into a different number. But these infinite, non-terminating decimal expansions can do nothing but change, i.e., it is an inherent part of what they are to be changing, and this can never stop – every time another number is added at the end of the decimal expansion the value of this “number” that the decimal expansion is supposed to be equivalent to changes, and because the decimal expansion is infinite, this changing will never stop, i.e., this decimal expansion will never have the only essential quality of being a number, viz., that of being a fixed, unchanging magnitude. Therefore, as noted above, it is not appropriate to call these decimal expansions numbers at all. We may gloss over this by saying that each time a number is added to the end of the decimal expansion, the magnitude added is approximately one-tenth that of the magnitude of the previous addition, and that this quantity becomes “infinitesimally small” as numbers keep getting added and as the decimal expansion gets nearer to the limit of the fixed number it is approaching. But we only react this way because in mathematics we are so accustomed to thinking of infinity in terms of the familiar concepts of infinitesimals and limits that in making this counterargument we are not as aware of the significance of the fact that an infinite decimal sequence cannot ever reach its fixed, finite limit point as we imagine ourselves to be. The limit is, by its nature, a point that a sequence always approaches but never reaches. An infinite decimal sequence is like a rational function, or the trigonometric tangent function, and its limit point on the real line is like the asymptotes in the Cartesian plane – we may say that “at infinity” the curve “touches” the asymptotic line, but of course the reality is that “infinity” is literally that – infinity, i.e., that which can never be reached, never completed. The only reason we are able to say that a sequence ever “reaches” its limit is that, as discussed in the previous section, for our typical practical purposes, whether scientific or mathematical, it has been sufficient to treat the concept of Euclidean distance and the concept of an infinite sequence of points of zero length as if they were the same, even though these two things are fundamentally different; i.e., it has been sufficient in many cases to use an approximation to the truth based on a, frankly superficial, similarity between these two things – the idea of an infinite decimal sequence “reaching” its finite limit point does not cause us any distress because we can clearly see that the finite magnitude in the real world of Euclidean distance and scientific measurement matches a sufficiently fine finite approximation of this infinite decimal sequence, and we therefore have minimal incentive much, or all, of the time to be interested in things at a finer level – the remainder of the decimal sequence that extends out beyond our approximation point may simply be called “noise” or be “rounded off” and then ignored, if it is even thought about at all. But we must reach out to this finer level and accurately understand its nature if we are to answer the deeper questions.
The diagonal argument conflates Euclidean distances or magnitudes, which are fixed, unchanging points on the line, with infinite, non-terminating decimal sequences, which are never fixed or unchanging. In other words, it equates quantities with non-quantities, numbers with non-numbers. This is crucial. The diagonal argument conflates the fixed, finite limit point with the sequence of closer and closer approximations that lead up to it; this is the same thing as saying that the Cauchy sequence that approaches an irrational is equivalent to the irrational number itself, or that the sequence of rationals in a Dedekind sequence that lead up to an irrational is equivalent to the irrational – the reality is that these sequences are each an infinite set of points on the real line none of which is ever, or can ever be, equal to the fixed point that is the irrational itself; and the same goes for rationals whose decimal expansions never terminate. Because the approximations may get “as close as we like,” then in our minds beyond a certain point the infinite decimal expansion is “just, effectively, the same thing” as the limit point, i.e., we conflate two things that are not the same type of thing and that are incommensurable at a fundamental level, with each other and treat them in our mathematical investigations and proofs, and think of them, as if they were the same thing. The diagonal argument is supposed to tell us that the collection of real numbers is greater in magnitude than that of the natural numbers, but in reality it does not say anything about the real numbers. Real numbers are the finite limit points of these decimal sequences, not the decimal sequences themselves, and because each real number, i.e., each limit point, is a finite, unchanging, fixed quantity, which can unambiguously be represented in real-world Euclidean space as a fixed, unchanging length or magnitude, the entire collection of these limit points plus all numbers whose decimal expansions terminate, i.e., the entire set of real numbers, can be placed in one-to-one correspondence with the natural numbers. In other words, there is no difference in “cardinality” be-tween the natural numbers and the real numbers.
We may think about this a different way. What the diagonal argument actually does is place the natural numbers in one-to-one correspondence with infinite decimal sequences, but it is disguised as an argument that places natural numbers in one-to-one correspondence with real numbers, or a subset of them. But what each number in the index sequence in the argument actually corresponds to is an always-changing sequence of numbers, i.e., an always-changing magnitude, i.e., an always-changing numerical value, in which the changes never terminate because the decimal sequence is infinite. But this violates the initial assumption of the argument that each number in the index sequence is being made to correspond to a real number, i.e., an unchanging, fixed, finite quantity or numerical value. Since this is a contradiction in the initial assumptions of the diagonal argument, i.e., each element in the list is treat-ed by the argument as both a fixed number and a non-fixed, ever-changing number at the same time, it is not surprising that paradoxical “discoveries,” such as that there are “more” real numbers than natural numbers, result from these assumptions. In particular, while it is true that c, in the example above, is not in the original list of decimal sequences, we may not use this fact to conclude that there are more real than natural numbers, because c is itself not a number, but rather an infinite, i.e., never-ending, decimal sequence that approaches, but never reaches, a number, i.e., a fixed, unchanging magnitude that can correspond to a fixed Euclidean magnitude or distance. Again, the concept of a limit in mathematics is an idealization that allows us to formalize the perceiving of a pattern in a sequence of numbers, the pattern itself being that the numbers in the sequence get arbitrarily close to, without ever actually reaching, a fixed, finite limiting point, i.e., the finite number to which the sequence approaches. But for most practical purposes, it doesn’t matter that the sequence never reaches the limiting point, so long as the mathematics allow us to make sufficiently accurate approximations to what it is the numbers are supposed to represent. And because we, as humans, seek to conquer the infinite, that is, to make it finite in an emotionally pleasing way, because doing so makes the infinite, and thus immortality in a crude but powerful emotional sense, attainable, we have a tendency to think of the concept of “limit” as “the point that the infinite sequence of numbers reaches ‘at infinity,’” and in this way we have, to a certain degree, finitized infinity, by giving ourselves a way to talk about infinity and think about it as if it were, in certain ways, a finite thing. But also, the desire to attain to infinity can easily make us de-incentivize, at a powerful emotional level, any thoughts or investigative work that might lead to the finding of an essential character of finiteness in something we thought was fundamentally infinite. These two forces oppose each other, which means that we are incentivized to finitize infinity, but to do so in a way that ensures that we have not completely finitized it, which would be emotionally dissatisfactory. So when we find or settle on something that seems to have some potential for solving this optimization problem, such as the concept of a limit in calculus, or the diagonal argument which seems to show that there are different levels of infinity, our minds latch onto such ideas and findings and incentivize us to conflate the finite with the infinite on the basis of these ideas and findings, because it is emotionally satisfactory to do so, and this emotional incentive makes it harder to understand or consciously think about the fact that such conflation is happening at all, much less to tease out the source of it. This does not mean, of course, that it is impossible to tease out the source of such conflation; only that it is more difficult, because emotionally distressing, to do so than it would otherwise be. The idea that an infinite decimal sequence can be equated with its finite limit point is both mathematically and emotionally useful, but we must remember that this equating does not correspond to any-thing in reality, because the limit points are always finite, while the infinite decimal sequences are always infinite.
As stated in the previous paragraph, it is not correct to say that the items in the list in the diagonal argument are numbers at all, since the defining characteristic of a number is that it is a fixed, unchanging magnitude, and is therefore always and inherently complete. Imagine a long but finite list of terminating decimal sequences, all in the open interval (0, 1). Given that all the elements themselves in this list are finite, i.e., they are terminating decimal sequences, no matter how far out any one of them might extend before reaching its termination point, then it is appropriate to call the elements in this list numbers, because each is a fixed, unchanging magnitude. It is therefore appropriate to identify each element in this list as an element in the list. The entire concept of an “element” of a list presupposes that what is called an “element” is finite, i.e., it is a whole, bounded, circumscribable thing which, as a whole, can be manipulated in various ways, such as being placed into a set as one of its members. This is why the concept of a set that contains itself53 is so troublesome to set theorists and philosophers – if the set itself is an element of the set, then if the element is finite this is a contradiction, because the act of placing a “copy” of the set into the set changes the set so that the copy is no longer a faithful reproduction of the original set; if, on the other hand, we desired to try to force the concept of a set that contains itself to not be a logical contradiction, then we would need to modify this element so that it contained a full copy of the original set as one of its elements – but then the original set will have changed again, so that though the original set is supposed to contain as an element a set that contains the original set as an element, the first-level element that is supposed to be a copy of the original set contains only one level down, not two, i.e., it contains an element that is supposed to be a copy of the original set, but this deeper element does not contain an element that is a copy of the original set, and so the first-level element is, in fact, still not a faithful copy of the original set. With each such attempt to nest further and further into this first-level element, the original set is changed, because one of its elements has now changed; but the first-level element will always be one step behind it, and so will never be able to be a copy of the original set. We might think to say that, like a finite limit point in calculus, “at the limit,” i.e., “at infinity,” the original set is finally faithfully reproduced by this first-level element within it. But, as with the limit concept in calculus, this would be a logical error, because infinity, by definition, can never be completed, i.e., no “infinity point” can ever be reached. If we stretched the analogy a little, we might say that the most that this progression could ever hope to achieve is that the element of the original set that is supposed to be an identical reproduction of the original set approaches, as closely as we like, to an identical reproduction of the original set, but never actually reaches it. For example, if at a certain point in this infinite regress we have gone through 5,000,001 levels of nesting, it will be the case that the first-level element and the original set differ by only 1 out of 5,000,001 levels of nesting, and are identical otherwise; but the limit point is still never reached by this progression of nesting, just as with a non-terminating decimal sequence, whereby no matter how many decimal numbers are added to the end of the sequence it will still never reach its limit point, i.e., regardless of the quantity of decimal numbers which have been added so far, an infinite number of additional numbers can still be added. Furthermore, for the concept of one set being equal to another to have any meaning, the two sets have to be finite, because only things that are finite, i.e., things that don’t change, can actually be compared. Thus, because to avoid the contradiction inherent in the keeping of this first-level element finite we are forced into an infinite regress, this first-level element that is supposed to be a faithful reproduction of the original set is always growing, which is, again, just another way of saying infinite, and which also means it is always changing; therefore, no actual comparison between this first-level element set, as a whole or a completed entity, and the original set, again, as a whole or a completed entity, can ever be made, since such a comparison is not meaningful. Note that this would be the case even if only one of the items we are attempting to compare was infinite; but in the case of this example, both are, because with each new level of nesting in this infinite sequence of nesting, both the original set and the first-level element are changed.
To continue the example, in the finite list of terminating decimal sequences that we have constructed it is, of course, possible to match natural numbers, starting with 1, in a one-to-one correspondence with the numbers in this list. Further, since this list is finite, the list of natural numbers that make up the index sequence for this list will be finite. Now imagine continuing to add more and more real numbers to this list, all with terminating decimal expansions. For each new number added, we increase the index sequence of natural numbers by 1. But for each number of decimal places, say 1 decimal place, 2 decimal places, 3 decimal places, etc., no matter how high the number of decimal places is we will always exhaust the entire set of numbers that can be in the given number of decimal places, i.e., such a list of numbers will always be finite. For example, the total number of numbers possible with only one decimal place in their terminating sequence, i.e., whose infinite decimal expansions contain nothing but 0s after the first decimal place, is nine – we leave out 0.0 because the open interval (0, 1) does not include 0. In the case of decimal expansions that terminate after only two decimal numbers, the total number of possible numbers is 99, again because we leave out 0.00. In the case of three decimal places, the total number is 999, in the case of 4 it is 9,999, in the case of 5 it is 99,999, etc. Notice that no matter how high the number of decimal places gets, this total number is still always finite, and these numbers can therefore still always all be placed in a one-to-one correspondence with a finite list of natural numbers. Further, if we order the numbers in the list so that all the numbers that terminate after only 1 digit are at the top, then below them all the numbers that terminate after only two digits, then below them all those that terminate after only 3 digits, etc., then this entire list, no matter how large it grows, can always be placed in one-to-one correspondence with the natural numbers. In fact, this is equivalent to saying that the natural numbers and the real numbers are both countable. Why? After all, we have only considered the reals in the open interval (0, 1). But the point here is that we are now listing numbers, i.e., each of the elements in the list is a number rather than an infinite sequence of numbers that never stops changing value, and so not only are the elements in the list precisely what they claim to be, viz., real numbers, no matter how many of these we add to our list we can always keep increasing the index sequence by 1 for each number we add. If we wished to add, for example, the numbers 0 and 1 to this list, so that the interval over which we are listing real numbers is now the closed interval [0, 1], we could do so simply by adding 0 and 1 to the top of the list. This does not change the cardinality of the list, because all we have done is bump the first number in the list, say, 0.1, down to the third position in the list, and all number thereafter have also been bumped down by two in the list, and thus in the index sequence. This is easily understandable, and it also does not give us any justification for saying that the list has somehow become greater than can be indexed by the natural numbers, since, again, the natural numbers are infinite, and can thus easily handle an increase of two beyond any point at which it might be at a given time in the indexing.
But what if we wished to add the interval (1, 2] to this list? This could easily be accommodated, first by adding 2 to the top of the list underneath 0 and 1, and then duplicating each number below this point that is already in the list, placing a 1 in front of it (e.g., 1.1 instead of 0.1), and adding this additional number just below the one its decimal expansion was duplicated from in the list. And if we wished to add the interval (2, 3]? The same procedure would suffice, and would suffice for all such intervals, positive and negative. But one might object that if one attempted to do this for all intervals, which is an infinite number of intervals, then one would never get beyond the natural numbers themselves, as the highest or first elements in the list; or, if one chose to add the natural numbers at some other point lower in the list, one would never get beyond first number in the first decimal place in the list, and thus would never reach even the second number in the first decimal place to continue this process for the rest of the numbers, including the natural numbers; e.g., in this latter case one would never reach beyond the “.1” decimal expansion in the list, because it would take an infinite number of numbers, 1.1, 2.1, 3.1, 4.1, 5.1, …, before we would be able to get to the point of adding the numbers for the next single-digit terminating decimal sequence, e.g., 1.2, 2.2, 3.2, 4.2, 5.2, … . But this is to miss the point. This is to fall back into the same logical error that makes the diagonal argument seem valid in the first place. The point here is that no matter what number is added to the sequence at any given time, or in what order the numbers are added, the numbers being added are always finite, and therefore it is always justified to call them numbers. Further, these numbers are always added to the list one at a time, and so, since the natural numbers are infinite, there will always be yet another natural number that can be assigned as an index number to the next real number that is added to the list, however we might choose to interleave the numbers in the list when we add them. The objection takes the “whole” or the “entirety” of the numbers 1.1, 2.1, 3.1, 4.1, 5.1, … and tries to reason about this entirety as if it were a unitary, completed thing, but this is a logical mistake because an “entirety,” a “whole,” is a fixed, unchanging thing, and this infinite sequence is, and will always be, non-fixed and changing. The point is that, unlike in the diagonal argument, the list that is created by our procedure involving terminating decimal sequences actually adds numbers to the list, i.e., fixed quantities, and since with each new fixed quantity added to the list yet another natural number in the index sequence can be made to correspond to it, no matter how large the list grows the index sequence will grow by exactly the same amount. Furthermore, note that no matter how large the list grows, the list will always be finite, i.e., it will never “reach” the point of infinity; i.e., it will never be a complete list of real numbers. Cantor made the mistake of assuming that the list in his argument was a completed infinite list of real numbers, i.e., an infinite list of real numbers that could be reasoned about and manipulated as a whole, and thus the diagonal argument is flawed for this reason too. To think that such completion is possible is, once again, to fall into the same logical error we have been discussing; as with the natural numbers, we are so used to treating and thinking of ℝ as a “whole,” an “entirety,” and reasoning about it as if it were a completed, bounded, circumscribable, unitary thing, that we don’t miss a beat when we assume that it is possible to arrange literally all of the reals, or an infinite subset of them, into a completed list that we can then attempt to analyze to determine its fixed properties, such as its cardinality or its cardinality’s relation to that of the natural numbers. But the ability to arrange all the pieces of something in the first place so that we may analyze and determine the fixed properties of the collective depends crucially on there being a finite number of pieces; since by definition infinity means to increase without bound, i.e., to always be adding elements or pieces to a given finite collection, it is never possible to have all the pieces of it such that they can all be arranged together, in a list or in any other way, in order that the fixed properties of the collection as a whole may be analyzed or determined; such a conception is specious. There can only ever be the finite. At most we may determine the properties of the pattern which produces the elements in the list; we cannot determine the properties of the entirety of the list itself, treated as a completed thing, because the list can never be an entirety whose inherent or unchanging properties can be determined. This is a crucial difference to keep in mind. The one-to-one matching between the reals and the naturals that we have spelled out using terminating decimal sequences works precisely because it represents the reals as what they are, i.e., as numbers, and it does not presume to capture infinity in a finite shroud, in any way. Once it is grasped that such capturing, in any form, is logically flawed, and thus impossible, the confusion begins to abate, and we begin to see how it is possible to make sense of things again, instead of continuing to concoct more and more elaborate schemes that ultimately do nothing but more deeply bury the fact that the foundation on which such schemes are built is hollow.
The diagonal argument rests on a misrepresentation of the real numbers, as well as on the flawed assumption that it is possible to have a completed set that contains an infinite number of elements, i.e., in both cases on a misrepresentation of infinity. It is because of these misrepresentations that the diagonal argument seems to give us reason to believe that multiple levels of infinity exist. Once we believe this, it is not a great leap to say that, though we do not know exactly how, nonetheless somehow the entire set of natural numbers, infinite though it is, must be “finite” in at least some sense, because the diagonal argument “shows” that there is a level of “quantity” of some kind beyond or above that of the natural numbers, and so it must be that the natural numbers, in some way, “end” at some point, so that it is then possible to go beyond them. But if the diagonal argument is flawed, then the entire basis on which we place our faith in the concept of multiple levels of infinity becomes nothing more than a grand illusion. The diagonal argument depends crucially on our willingness to gloss over the essential difference between an infinite, always-changing magnitude, on the one hand, and a fixed, unchanging magnitude on the other, and, in fact, depends crucially on our being so inured to this glossing over that we hardly ever, if ever, think about this essential difference in a nontrivial way or consider it worthy of notice. But when something walks like a duck, quacks like a duck, swims like a duck, etc.,54 especially over the course of almost 150 years of intelligent, driven people trying to prove that it is not a duck, chances are that there is something amiss in how we are perceiving things, and thus chances are we may be able to solve our longstanding problem by allow ourselves to consider the possibility that something more foundational needs adjusting.
Before we close this section, let us look at some additional ways by which we may see the flaw in the diagonal argument. First, consider the sequence of numbers 0.1, 0.01, 0.001, 0.0001, … . We can see that the finite limit point of this sequence is 0, although, as we know, because this sequence is infinite, it can never reach its finite limit point. Now imagine these numbers as representing Euclidean measures of distance, say, inches. But no matter how many times we iterate this sequence, the Euclidean distance will always have a non-zero, positive measure, though after a point, of course, even our most precise scientific tools would not be able to measure any further changes in magnitude. Now imagine the infinite decimal sequence 3.99999… . Is this sequence equal to 4? Could it ever be equal to 4? The answer is no, because no matter how many 9s we add to the end of this decimal sequence, the sequence of numbers 3.9, 3.99, 3.999, 3.9999, … will never reach exactly 4, even, assuming these numbers represent Euclidean distances, far after we are unable to distinguish one measure of distance from the next using our most precise scientific tools. Again, an infinite sequence can never actually reach its limit point. Further, since any sequence such as these never ends, then no matter how far out we take it, a given such sequence as a whole can never be a fixed number that can represent a fixed Euclidean distance, i.e., the Euclidean distance for these “numbers” can never actually be measured. But such a measurement is precisely what the diagonal argument claims is possible, when it equates non-terminating decimal sequences with fixed real numbers. The diagonal argument claims that it is possible for a fixed, unchanging magnitude to simultaneously be a permanently unfixed, always-changing sequence of numbers. This is, of course, an absurdity.
Second, we may think of the diagonal argument as saying that we have found an infinite sequence of numbers that is “different” from all other infinite sequences of numbers in the given list, rather than that we have found a particular number that is not in the list of numbers given. But even this is flawed, because, as we have discussed, unless quantities are fixed, they cannot be compared, and so it is impossible to determine if they are the same or different, i.e., such a determination is not meaningful; at most we may say that the particular finite diagonal number obtained up to a certain point in the diagonal process is different in one or more decimal places from each of the finite list of numbers with the same finite number of decimal digits traversed up to this point, and in this way we may say that no matter what the decimal numbers are beyond this point, the diagonal number will never be equal to the number or numbers with which it differs in one or more of the earlier decimal places. But notice that in this conclusion we are ignoring the infinite nature of the decimal sequences, because we do not need to consider their infinite nature to determine whether these particular finite decimal sequences are different; we are, in other words, not actually comparing the two infinite decimal sequences, but finite approximations of them. The infinite decimal sequences in the diagonal argument that are supposed to represent real numbers can never be compared in this way, because each of these sequences is always changing value, and in order to compare two numbers to determine if they are different, they must both have fixed values – in the comparison above, not only do the decimal sequences being compared have to themselves be finite in number of digits, but each digit in each decimal place must also be finite, e.g., a prerequisite for determining if two finite decimal sequences differ from each other in the 5th decimal place is that the number in the 5th decimal place of each decimal sequence be unchanging, i.e., fixed. If the number in the 5th decimal place of one or both of these sequences was constantly changing, then it is easy to see that the two finite decimal sequences could never have their magnitudes compared to determine if they are the same or different. It is like having a list of single-digit elements, and then having a number that is not in the list, but with the condition that an inherent property of each of the elements in the list, as well as of the number not in the list, is that the value of the number keeps changing, i.e., never stops changing; it is clear that it is impossible to determine if the number that is not in the list matches any of the numbers in the list, because such determination requires that all numbers being compared be fixed in value, but since the values of the numbers involved are permanently changing, they are never fixed and thus can never be compared; it is, in fact, not valid to call these ever-changing entities numbers at all. However, the diagonal argument does exactly this, just in a way that is not as blatantly noticeable and absurd: it maps each natural number in the index sequence not with a single, fixed real number, as it claims to, but with an infinite number of different numbers; this has the result that for the first, say, 10 elements in the list, there are supposed to be exactly 10 numbers, but since each element can change its numerical value any number of times, we may say that there are more than 10 numbers in the first 10 elements, so that even after we have accounted for the first 10 numbers, we may say that each element has changed value, so actually there are 20 numbers in the first 10 elements, and we must therefore go back and account for these as well; but then, each element may change again, and again, ad infinitum. By treating each real in its list as a non-terminating decimal sequence, the diagonal argument creates the conditions which allow this kind of never-ending single-element value-changing to take place, i.e., it creates the conditions which allow each fixed, real number to be treated as if it were an infinity of different real numbers. But this is clearly not what we are told the diagonal argument does, viz., assign each natural number in the index sequence to a single, fixed real number. In other words, the diagonal argument is not what it is claimed to be. Given this, it is not surprising that the diagonal argument can be used to “prove” that there are more reals than naturals, since it is able to say, first, that it has for each element of the list mapped a particular natural number one-to-one with a particular real, and second, that, at the same time, each of these naturals is not mapped one-to-one to a particular real, but rather one-to-many, and, in fact, one-to-infinitely-many. If we first assume that each natural is mapped to a single real, and that all the naturals are accounted for in this way because the sequence of reals being indexed is presumed to be infinite, but then add on top of this that there are now suddenly more reals than what were previously listed because each natural number can be mapped to a different real than it was originally mapped to, then of course if the “totality” of the naturals is “already accounted for” by the original list, the addition of new real numbers on top of this would mean that there must be “more” reals than naturals. However, this argument is flawed, because it treats the set of naturals, which is infinite, as if it could be completed, and, as we have been discussing, it treats infinite, and thus ever-changing, sequences of numbers as if they were equal to single, fixed, finite quantities. The diagonal argument contradicts itself by saying first that naturals and reals are mapped one-to-one in its list, but at the same time implying, and making essential use of this implication, that the naturals are, in fact, not mapped one-to-one with the reals in its list, but one-to-many.
A valid version of the diagonal argument is one which is restricted to a finite list of terminating decimal expansions – we may take the diagonal and change each number in the resulting sequence to something different, per the diagonal argument, and then conclude, correctly, that the resulting number is different from every number in the list. But the flaw in the actual diagonal argument is that it does not appreciate the fact that this process of taking the diagonal and changing each of the resulting numbers cannot be extended to an infinite list of infinite decimal expansions, because doing so conflates the finite with the infinite, and therefore does not make logical sense; in such an effort, in the traversing of the diagonal of the list we would be attempting to obtain a number that we could then compare with the other numbers in the list whose diagonal we are taking. But (a) we would never be able to obtain a number from this infinite diagonal process – remember that an infinite sequence is not, and can never be, equal to its finite limit point – which we could then compare against the numbers in the list, and (b) the “numbers” in the list are not numbers anyway, since their magnitudes are always changing, i.e., each element in the list will never stop changing, and so it is meaningless to try to compare the “magnitude” of one of these “numbers” to another magnitude. The diagonal argument makes the mistake of assuming that because a process, i.e., the taking of the diagonal of a list of decimal expansions and producing a number as a result, makes sense when all pieces involved are finite, it is therefore legitimate to conclude that this process must also make sense when we are considering an infinite extension of these pieces. But this is to make the logical mistake of conflating the finite with the infinite and treating them as if they were the same thing, when, in fact, they are not.
Another way of looking at this is the following. Each “number” in the diagonal argument is imagined to be entirely contained in the list of numbers, and this is represented by the ellipsis at the end of each decimal expansion which is meant to indicate that all the rest of the decimal digits for the given number are to be imagined as being included, even though they are not explicitly shown. In other words, it is implicitly understood in the diagonal argument that what is supposed to be included as elements in the list are the individual, singular, fixed magnitudes of the real numbers, i.e., numbers that can be mapped one-to-one with the natural numbers; it is simply that these numbers are being represented by approximating decimal sequences. There is nothing wrong with doing this, so long as we always remember that the ellipsized decimal sequence itself only represents the fixed limit point that is the real number, and is not and can never be equivalent to it. But if we are to treat the decimal expansion as if it were equivalent to its limit point, then this would mean that in order to ensure that the limit point is accurately represented as an element in the list by its decimal expansion, we would have to include the entirety of the infinite number of decimal digits in each element that we wish to treat as a real number, and this is, of course, impossible. The reason we feel we can get away with including only the first few numbers of the decimal expansion followed by an ellipsis and calling this ellipsized expansion a real number is that when we look at the decimal expansion we can easily see that it approaches a finite limit point, which makes it easy to conflate the decimal expansion with the finite limit point and conclude that we can treat the decimal expansion as if it were the finite limit point. We then proceed to make the diagonal argument based on the approximating decimal expansions, completely forgetting that the only reason we feel that the decimal expansion can be thought of and treated as equal to the real number which it approaches is the fact that the real number itself is a single, fixed, unchanging point, i.e., a finite, unchanging quantity that can clearly map to a single natural number, and that the decimal expansion approaches this fixed, unchanging point as closely as we like, making it as easy as we wish to conflate the two and treat them as equal. The diagonal argument exploits this false equality in order to represent the finite, fixed point of a particular real number as an infinite decimal sequence that is never, and can never be, fixed, in order to “prove” its result. But in order to represent the entirety of a particular real number, that is, the real number itself, by its infinite decimal expansion, as the diagonal argument claims to do, an infinite number of numbers would need to be written just to finish “adding” a single element to this list; then, beyond this, another infinite number of numbers would be needed to add the second element to the list, and then again for the third, etc. With the claim that each decimal expansion in the diagonal argument is equal to a real number, and can thus be treated for all purposes as if it were the real number which it approaches, the diagonal argument also claims that an infinite number of numbers can be written in a finite space and time so that the “full” non-terminating decimal expansion of a real number can be entirely encapsulated in a single, fixed element of the list. This is, of course, impossible, which is why in the diagonal argument the decimal expansions are always written with just a few initial numbers followed by an ellipsis. The structure of the diagonal argument itself implicitly acknowledges that its assumption that an infinite decimal expansion can be treated as being equal to the finite, fixed real number which it approaches is absurd. The argument, however, does not heed its own implied advice.
Yet another way of looking at this is the following. Imagine that, per the diagonal argument, we take the diagonal for an extended period of time, e.g., across 5,000 numbers, but we temporarily stop at this point. Then imagine that we change each of these 5,000 numbers in the diagonal sequence so that it is different from all sequences in the list of sequences that we have so far traversed, again, per the diagonal argument. We now know that the modified number is different from all of the first 5,000 numbers in the list, because it is different from the nth number in at least the nth position. But then imagine that the first 5,000 numbers in the sequence all terminate after 5,000 places, and that the diagonal number thus also terminates after 5,000 places. We would then have the situation in which the new number we have created from the diagonal is a number, i.e., a fixed, finite quantity, and we could correctly say that our new number is different from each of the 5,000 numbers in the list that we have run through so far. But then, imagine that we allowed the decimal expansions of these 5,000 numbers to increase by one, to 5,001 numbers, and also added a 5,001th item to the list. First of all, each of the first 5,000 numbers is now a different number than it was before we added the 5,001th digit to it. Second, the 5,001th item in the list could be exactly equal in its first 5,000 digits to our new diagonal number sequence, and, in fact, let us imagine that it is, and that it also has been extended by another digit to 5,001 digits. If we take the diagonal again, it will be 5,001 digits this time, and let us modify each digit in this sequence, add the new sequence to the list, and add another digit on the end of each of the now 5,002 items in the list. This process could continue as long as we like, one element and one decimal digit at a time. Now, if we did not allow the number of digits in each list element to be increased at each iteration after the first 5,000, then it would be possible to run through the same process a finite number of times before we had exhausted all possible changes to the diagonal, which would always be 5,000 digits in length, and added these new decimal sequences to the list; and this would be the case regardless of at which number in the list we started taking the diagonal, assuming that at any point in the process we wished to take a diagonal starting at a list element other than the first one. In other words, it would be possible to completely list, i.e., exhaust, all possible 5,000-digit sequences. But in the case that we are able to add another digit to the end of all decimal sequences upon each iteration of this pro-cess, then at each step the increase in the number of list elements it takes to exhaust the entirety of per-mutations of digits in sequences of that length is always overmatched by again increasing the total number of decimal places by one, though the overmatch at each step still always only allows for a finite increase in the number of numbers that can be added to the list. What this means is that if the decimal expansions that we are approximating more and more closely at each step are non-terminating, then this process can never end, i.e., we will never be able to include all numbers in the list, and instead will only ever be able to grow the list beyond what we have already grown it up to a given point. Further, since it is clear that this process can never end, it should also be clear that with each iteration of the process we are changing the value of the number in each position of the list, i.e., we are changing the number that sits at each position of the list.55 But this violates one of the initial assumptions of the diagonal argument, viz., that each number in the list is unchanging, i.e., that it is a number. The implication of the diagonal argument is that when the diagonal is being taken it is being taken across a list of numbers, but actually it is being taken across a list of always-changing, always-growing sequences of numbers. The diagonal argument treats each fixed, finite real number as an infinity, which is a contradiction. Imagine that instead of adding a single sequence of digits to the list after taking the diagonal at each step, we decided to add all possible sequences of digits of that length – say, 5,000 – at that one step, and then add an equivalent number of digits to the endpoints of all decimal sequences in the resulting list so that the list is again “square” before we take the diagonal again, and thus the next diagonal will still traverse all element in the list. But no matter how many times we perform even this modified, “upgraded” process, we can always perform the process again. Because we can always extend the decimal place of each element of the list by one, no matter how far we have already extended it, then we can always come up with new numbers not already in the list. But this fact is not the result of the “uncountability” of the reals. It is the result of the fact that at every iteration of the process of taking the diagonal, when we add digits to the end of the elements in the part of the list that we have already run through we are effectively adding net new capacity to the list for the production of numbers, i.e., capacity for the production of numbers that did not exist before in the elements of the list we have already traversed, and implicitly assuming that this net new capacity is also available in all subsequent elements we add to the list; and we do this even though we assume that both the numbers we have already traversed and those we have not yet traversed are fixed from the beginning, i.e., that they never change, since they are assumed to be numbers. And because these decimal sequences are non-terminating, this adding of net new capacity for the production of numbers never ends. A real number itself, however, is finite, and thus is a representation of something which has terminated, i.e., has ended. It is a logical error to equate these two types of thing, one inherently infinite, the other inherently finite. Finally, it is important to emphasize that no matter how many steps, how many iterations, of this process we go through, it will always be the case that the total number of numbers added at each step is finite, and can thus be mapped one-to-one with the natural numbers; and since the natural numbers are infinite, this process will never exhaust the natural numbers. In other words, Cantor’s argument is able to “show” that the total number of reals exceeds the total number of naturals because what the argument treats as a single, fixed number actually has the capacity to be forever changing, forever growing, and so since within a single element of his list it is possible to map the digits of this element one-to-one with the natural numbers out as far as we like, this process of one-to-one mapping will never complete even for the first element of the list. But if we then assume that somehow it can complete, so that we are then able to write down a second element in the list that is also non-terminating, then a third after the second one completes, then a fourth, etc., then we have already implied, i.e., already built into the setup of the argument, the result that we subsequently obtain, viz., that the reals are greater in number than the naturals, because we have already assumed at the outset that it is possible to extend the concepts of number and quantity beyond the “end” of the natural numbers. This is a circular argument. Nothing can be proved true by first assuming that it is true, however implicitly and subconsciously we assume it. And since it is impossible to extend beyond the “end” of the natural numbers, given that the naturals, being infinite, have no “end” to extend beyond, the initial setup of the diagonal argument is flawed. It is no surprise, then, that a logically impossible conclusion results from the argument.
Another way of looking at the flaw in the diagonal argument is by reversing the position of the decimal place in each of the numbers in the list, i.e., instead of the decimal place always being on the left of the expanding sequence of digits, have it be always on the right. In this way, it is clearer, i.e., more obvious, that the argument is flawed, because each time we add a digit to the left of this left-expanding sequence of numbers, it is obvious that the magnitude increases by a factor of 10, and we can clearly see that the expanded sequence of numbers for a given element in the list is a different number than the number which that element was before we added the left-most digit. Further, we can clearly see that the new number is, from the perspective of what is normal and familiar to us, substantially different in magnitude compared to the previous number that the same element was at the previous step, and these differences for a given list element multiply rapidly as we perform more and more iterations of the process. Clearly, if each element in this list of numbers is supposed to be a number, i.e., a fixed, unchanging magnitude, then we are way off base in thinking that an infinite, ever-left-expanding sequence of numbers could fit this bill. But when the decimal point is on the left, and the sequence of numbers is ever-right-expanding, we do not notice that the same argument applies. And the reason we do not notice is that, instead of each step in the process increasing the magnitude of the change by a factor of 10, each step in the right-expanding process decreases the magnitude of the change by a factor of 10, and also that the left-expanding process, as would be said in calculus, “diverges to infinity,” while the right-expanding process gets ever closer to a finite limit point. These outward differences, combined with a powerful need to finitize infinity in an emotionally appealing way, can completely mask the fact that in certain essential ways these two expansions are the same, i.e., they are both infinite sequences that never reach their limit points, and can thus never logically be equated to their limit points – in the left-expanding case to the limit point of “infinity,” which can never be reached, and which itself is not a fixed point that can be approached anyway, and in the right-expanding case to the limit point of the finite number which the sequence is approaching. If we agree that a single list element in the left-expanding case can never be equal to, and thus treated as, a fixed, finite number, then we must conclude that this is true for the right-expanding case also.
Yet another way of looking at all this is that the diagonalization procedure is itself a pattern that is specifically designed to produce a sequence of numbers that is not in the list of number so far traversed. Because the earlier decimal places are explicitly changed to be different from the earlier decimal places of all numbers so far traversed, then just by a comparison of these earlier decimal places we can know that the new sequence is different from all the previous sequences. If we then switch to thinking of the fixed limit points instead of the infinite decimal sequences that lead up to them, we can also see that the new fixed limit point is different from all previous fixed limit points, and therefore, in terms of numbers, this new number is different from all previous numbers. Because the pattern of producing these new numbers can be repeated as many times as we like, then no matter how many times we execute this pattern, a number different from all numbers traversed so far in the list will always be produced. However, we are unjustified in saying that there can be anything more than this; in particular, we are unjustified in saying that this process can somehow complete the accumulation of a countable number of repetitions of this pattern, so that the “new number” that is produced by this final repetition is now “beyond” the ability of the natural numbers to index. By explicitly designing a pattern, the diagonalization pattern, in order to ensure that every time the pattern is applied a new sequence of digits or a new number is produced that was not already in the list, all we are doing is ensuring that each time the pattern is applied we create something that did not exist in the previous finite list of things, i.e., we are adding one more unique thing to a finite list of unique things. But no matter how many times we do it, adding one more thing to a finite list of things can never accumulate enough things to “surpass” the “totality” of the natural numbers in terms of number of things. The desire to conquer the infinite made Cantor, and makes modern set theory, conflate a pattern that can be applied as many times as we like with the infinite sequence of things produced by the pattern, and then conclude that the latter can be completed because the former can be. But since a pattern can be applied as many times as we like, there is no end to the number of possible applications of the pattern, and also no end to the number of natural numbers that can be used to index applications of the pattern.
Also, the key components of the diagonal argument can be used to prove that the natural numbers are uncountable. The argument says that because a pattern can be found that produces a number that is not in an existing countable list of numbers, this new number must be “beyond” the countable, and thus must be proof of the existence of the uncountable. But if we take the even natural numbers, which is a countable list of numbers, we may use this argument to say that since the number 3 is not in the given countable list of numbers, this must mean that the existence of the number 3 is proof of the existence of the uncountable – after all, all natural numbers are already “accounted for” by the process of indexing the countably infinite sequence of even numbers. The only reason we do not treat this as a valid argument is that it is clearly perceivable that there is a pattern that allows us to index both the even numbers and the odd numbers together as one countable sequence. On the other hand, the inclusion of the erroneous but implicitly accepted concept of finitized infinity, in the form of infinite decimal sequences that are treated as being equal to their finite limit points and the supposed logical validity of the concept of the completed set of natural numbers, combined with the fact that many reals can only be represented in decimal form by infinite decimal sequences, confuses matters when it comes to the reals, so that in the case of the reals it is no longer clear or obvious that the infinite sequence with which we are dealing is countable. This lack of clarity then provides opportunity which did not exist before to find a way to “prove” something that is impossible but emotionally comforting, should a person, e.g., Cantor, feel the desire or need to do so. But the reality is that once the logical errors and misconceptions that create this lack of clarity are removed, we are left with the fact that the reals, being fixed magnitudes each and all, are also countable; in other words, the clarity that makes us conclude that the argument given above for the evens and the odds does not prove that the natural numbers are uncountable becomes the same clarity that allows us to conclude that the real numbers themselves are also not uncountable.
This part briefly covers some of the broader implications of the clarification of concepts and the resolution of the continuum hypothesis that were presented in the previous part. We discuss things such as the Banach-Tarski paradox, Skolem’s paradox, infinitesimals and the hyperreals, the Cantor set, and numerous other topics for which the conclusions in this paper are relevant. We begin with a discussion of the nature of the continuum.
What is the continuum? In set theory and real analysis it is equivalent to the set of real numbers, typically envisioned as points or positions in a linear sequence with no gaps that is infinite in both directions, i.e., a line. We can then take certain subset of reals, such as particular finite sets of numbers, the natural numbers, the rationals, irrationals, algebraics, transcendentals, primes, square roots, etc. We can, in fact, take as many subsets, either mutually overlapping to one or another degree, or all mutually disjoint, of the reals as we like. But in light of what we have learned in this paper, there are certain things we can say about the continuum, or parts of it, that will allow us to clear up the confusion that has persisted since the idea of the continuum was first conceived, with regard to its supposed nature and how to define it. The problem of defining the continuum fully and clearly, i.e., in a way that does not always leave at least some things about its supposed nature seemingly intractably unclear, is caused by the same logical error that makes CH so difficult to wrap our heads around – we have, without realizing it, conflated the finite and the infinite, and we treat them, in various ways, as if they were the same thing. This conflation is a logical contradiction, and any mathematical (or philosophical) statement or theorem or proof that is based, partly or wholly, on this contradiction will itself be flawed and contradictory, and will, in idiosyncratic ways dependent upon the particular details of the statement and its subject matter, persistently defy satisfactory clarification of its meaning by what, for all we can tell, is sound, rational intuition and perception.
Let us then turn, in the next three sections, to some specific concepts related to the continuum.
Can the continuum actually be a line, i.e., an idealized gapless form of single spatial dimension and infinite length in both directions? For that matter, can a subset of the continuum be a line segment? The answer, as we have already discussed, is no, because this is a logical contradiction; even the smallest segment of a line we could possibly imagine would still be too large a stretch of length for any amount of zero-length points to accumulate to its length, since such a string of points cannot accumulate beyond exactly zero length. Any attempt to make the definition or concept of a real number more precise, such as with Dedekind cuts or Cauchy sequences, will always be insufficient to solve the problem of how we are to make a non-zero, positive magnitude equal to what can only always be a zero magnitude, however useful such a conflation may be as a practical conceptual tool in various mathematical contexts. By defining each irrational by the use of an infinite sequence with smaller and smaller differences or an infinite sequence of rationals, we make a little clearer the fact that to represent an irrational exactly in a numerical way requires an infinite sequence, and as such we cannot ever represent an irrational exactly by any finite numerical means; but at the same time we also make it conceptually easier for us to close the gap between the finite and the infinite for a given irrational number. We may do the same, if we like, for rationals whose decimal expansions do not terminate. And it is this closing of the gap between finite and infinite, i.e., the finitizing, or conquering, of the infinite, that we, as human beings built by the evolutionary process, greatly desire. This desire gives us a strong emotional incentive to ignore the fundamental difference between the finite and the infinite if we can find a way to make the difference seem insignificant. If we are able to do this, we can feel at least reasonably comfortable with the idea that there is no essential problem with concluding that an infinite sequence of zero-width points is able, somehow, to line up to a positive, and indeed any positive, measure of Euclidean distance; since the infinite decimal sequences we are considering are infinite, and thus as we proceed out to greater and greater decimal places they make ever more minor corrections to the value of the number at any given point, we can imagine that these sequences “eventually” close the gap with the points immediately on either side of them, and this then helps give us a sense of justification in saying that we have a continuous line of positive length made up of a sequence of zero-length points. The fact that we know that, technically, a point is of zero length and thus that a line is only an idealized representation of the real numbers does not necessarily mean we grasp the deeper implications of this understanding. An idea can be known at multiple levels, and each deeper level allows for a fuller, more intricate and nuanced, and more complete understanding of the idea than do the shallower levels. In fact, it is the psychological process itself of “closing the gap,” in a more general sense than that just specified regarding the real line, that allows us to feel justified in not digging deeper to seek out the fuller meaning of an idea, i.e., that makes us feel satisfied that our shallower-level knowledge is all the knowledge that is useful to have about the subject; since we have closed the gap comfortably in our minds, we have much less incentive to dig deeper than we would if we still felt that we were faced with an unsolved problem.
Let us now elaborate on the essential difference between a geometric line and a linear sequence of zero-length points. The real numbers themselves (as opposed to infinite sequences which lead up to but never reach them), which are always finite (since each number, without exception, is of fixed magnitude), are always only positions, and thus have zero length; therefore, they cannot ever accumulate to a line, however small, of positive length. Also, if we treat non-terminating decimal sequences as if they were equal to the real numbers which they approach, as the diagonal argument does, then since these decimal sequence do not terminate, i.e., are infinite, we will never be able to locate a fixed point on a line to which this infinite decimal sequence is supposed to be equal, since no matter how far out in the decimal sequence we go, the addition of yet another digit in the decimal sequence will cause the real “number” to yet again change position on the line. Therefore, if we treat each non-terminating decimal sequence as if it were the real number which it approaches, we will never be able to line up the points in the way that they are imagined to be lined up in order to create the real line, since for this to happen each preceding point must be fixed in position for another point to be added next to it, and the point added must also be fixed in position; but, in the case of real numbers whose decimal expansions do not terminate, if these real numbers are treated as being the same thing as their infinite decimal representations, the preceding point will never be fixed, and neither will the point being added, and thus, gaps between different numbers on the real line will always exist, no matter how close the infinite decimal sequences are to each other, and it will be the case that either the magnitude of the distance between two “successive” points on the line will be always changing, or else the two points will be the same point, in which case they are not two successive points at all. This itself is a symptom of the fact that points are of zero length, and therefore (a) there is no time at which two successive points, i.e., different points near each other, treated as infinite decimal sequences that start at different places, will “meet” in perfect continuity with each other and remain in this stable and fixed relation thereafter, and (b) even for points treated as fixed positions, rather than as infinite decimal sequences, they can never meet in perfect continuity and yet still remain two separate points; if they meet in perfect continuity, they become the same point, and thus relinquish their status as separate numbers. If we, therefore, think of infinite decimal sequences as being equal to real numbers, as the diagonal argument does, it is more appropriate to say that the real “line” consists of the following: (1) points that are fixed, which are those numbers whose decimal expansions eventually terminate; these fixed points may be spaced out according to a one-to-one mapping between them and their Euclidean distances from the 0 reference point; and (2) points that never settle down, and thus are always bouncing around, however restricted in range this bouncing becomes for any given infinite decimal sequence, and this include both irrationals and rationals with non-terminating decimal sequences. But even with this description, in which the reals are represented partly by fixed points and partly by ever-bouncing points, note that the only actual numbers are the fixed points; the ever-bouncing points are not numbers at all since they are never of fixed magnitude. Furthermore, the limit points which the ever-bouncing points approach but never reach are themselves fixed points, though we have not yet included these particular fixed points in the above description of the real line. But since the limit points themselves are fixed points, they, too, can be considered numbers. In other words, the only entities that may legitimately be called numbers are the fixed points, i.e., the terminating decimal sequences, and the limit points that the non-terminating decimal sequences approach; and note, as we discussed earlier in a different context, that each of the fixed points in the sequence of points of a particular infinite decimal sequence is itself a fixed point with a terminating decimal sequence, and thus is already included in our list of legitimate numbers. But since this covers all the real numbers, and since they are all fixed points on the real line, what this means is that the real numbers and the natural numbers can be placed in one-to-one correspondence with each other. Also, this way of describing the real line means that though the points are spread out in a linear way as far as we like in both directions, and are dense, still because each point is a point, there is literally nothing that we have spread out, i.e., the real “line” not only never finishes filling out, which is necessary for it to be considered continuous, it never starts to fill out. So, the real line can be thought of either as a linear sequence of positions that are spread out from each other by various fixed Euclidean distances and that extend as far as we like in either direction, but with the caveat that the positions, or points, never touch each other no matter how close they are to each other, and thus that the line itself is never continuous anywhere; or as nothing but a single position which, no matter how many other “positions” we add “next” to it will always remain in total of exactly zero Euclidean length. In either case, a line, as we understand the term from geometry, is never built, and never can be.
Because the real numbers are infinite, it is never possible to bring together, in one finished collection, all the real numbers, and since we are accustomed to treating and thinking about the reals as a finished set or finished thing and to thinking that we can string them together as a one-dimensional geometric line, the idea that neither of these things is possible can be counterintuitive. But it can also be emotionally distressing; in a certain sense the realization of this impossibility is tantamount to giving up a nontrivial measure of certainty and security in life. Also, the above ideas imply that it is no more or less difficult to aggregate all the real numbers together into one completed entity than it is to aggregate all the natural numbers together into one completed entity. Each of these represents infinity, and infinity is singular and unitary, not something that can be split into different types or levels; thus, each collection is equally incapable of becoming a completed entity, rather than the one being, in some nebulous sense, more incapable than the other. Our desire to conquer infinity, to finitize it, constantly spurs us to try to become as comfortable as possible with the logical error of equating the finite with the infinite, in this case by trying to make the set of reals correspond to a geometric line. Also, the practical usefulness of this equating makes it that much harder to backtrack, i.e., to see the logical error for what it is.
It is said that rationals are dense in the reals, by which we mean that between any two rationals, no matter how close they are to each other, there is always at least one other rational. Of course, this is true so far as it goes. But the truth of this depends crucially on the fact that numbers represent only positions on an imaginary line, and are of zero actual Euclidean length. So even though there is an infinite sequence of rationals between any given pair of rationals no matter how close to each other, if we were to try to “connect” them together so as to make the sequence of rationals a continuous line, we would not be able to do so, not only because there are infinitely many irrationals between any two rationals on the real line, but because even if we were to imagine removing all the rationals and trying to place them into a continuous line by themselves, since they are points of zero length it would be impossible to create any length of line at all in this way, no matter how small. Furthermore, even though there is an infinite number of irrationals between each pair of rationals, adding the irrationals to the rationals would not make the linear sequence of points continuous because, again, each number is a fixed, zero-length position (of course, treating numbers with infinite decimal sequences as their fixed limit points), whether rational or irrational, and so collectively they would still only be of zero length. In other words, fleshing out the rationals with the irrationals to create a line of non-zero, much less infinite, length with no gaps is impossible, even though the rationals plus the irrationals together make up all the reals. In fact, trying to create a continuous line by adding the irrationals to the rationals is yet another example of trying to finitize the infinite, in this case by treating an infinite sequence of zero-length points between any two rationals as if collectively they could become a particular finite segment of a geometric line after they had been completely aggregated. In relation to this, we may also say that in the above example where we imagined taking all the rationals out of the real line and trying to line them up, this task itself is impossible – there are an infinite number of rationals, and taking “all” of them out of the real line means we have taken the “complete” set of rationals out of the real line, but an infinite set can never be complete. Another way of thinking about this is that no matter how much we magnify smaller and smaller segments of this linear sequence of positions, we will always see that points are still being added in the linear sequence within those smaller and smaller segments, i.e., that the process of adding points to this linear sequence can never complete, because if we stop at any point, the total set of points would be finite, and so if we were to imagine that this infinite process actually “completed” within a given segment, we would be conflating the finite with the infinite, i.e., we would be concluding that the infinite process of adding more and more points to the linear sequence has somehow completed in the creation of a continuous segment of line and a total number of points, i.e., has somehow become finite. And, as we have learned, any attempt to finitize the infinite will inevitably en-counter flaws, errors, and contradictions. Note also that the same argument applies with the division of the reals into the algebraics and the transcendentals, or any other possible division. The real line, in other words, is not a direct or fully accurate representation of what we call the “real numbers,” but, at best, a useful approximation of them.
An infinitesimal is defined as a non-zero, positive quantity that is, nonetheless, smaller than any other positive quantity. But right away we can see that if we treat such an entity as a fixed quantity, i.e., as a number, we involve ourselves in a contradiction. It is impossible for this entity we are calling an infinitesimal to ever stop at a fixed quantity, because as soon as it does we may point to an even smaller positive quantity that it is larger than, thus contradicting the definition of infinitesimal. But then since an infinitesimal must always be decreasing and getting closer and closer to zero in order to avoid a contradiction, its magnitude will be forever changing, and thus it is not appropriate to call an infinitesimal a number. In fact, strictly speaking, the definition of infinitesimal contains a contradiction within it, and so based on this definition the concept of an infinitesimal is logically incoherent, and so not meaningful.
It is the same with the δ-ε definition of a limit, but from a different angle. With the δ-ε definition, we say that for a point (c, L) on a curve56 in the Cartesian plane, “the limit of f(x) as x approaches c is L” is equivalent to saying that for every positive ε, no matter how small, there exists a positive δ such that if x is within δ of c then f(x) is within ε of L. Because ε can be as small as we like, so long as it never reaches zero, we can get as close as we like to L along the curve. However, as with a non-terminating decimal sequence, this process of taking smaller and smaller ε can never end, because we have specified that x can never be c, but can only approach c, i.e., that ε can never reach 0. Similarly, f(x) can never reach L, but can only approach L. The fact that we think of the unique tangent line at that point on the curve being “finally reached” by ever-closer approximations to this tangent line, or of the point f(x) = L on the curve being “finally reached” by the infinite sequence of approximations of closer and closer points on the curve, is an artifact of the switching over in our thought from the infinite, in the context of infinite sequences, to the finite in the context of Euclidean position, distance, and slope measures. By saying that the infinite sequence of lines through pairs of points on the curve that get ever closer together can actually reach the tangent line at L, and by saying that x, as it approaches c through an infinite sequence of smaller and smaller ε, can, “at infinity,” actually be equal to c, or f(x) equal to L, is to conflate the finite with the infinite, and thus to involve oneself in a contradiction. Calculus is useful not because it actually conquers the infinite, but because, as with the idea that if “enough” points are accumulated linearly they will “eventually” close the gap and create a continuous line, the logical error of conflating the finite with the infinite is, in calculus, insignificant, and thus irrelevant for the purposes for which calculus is used, viz., the production of results that have a nontrivial practical value in helping us predict and explain patterns of structure and behavior in real-world phenomena.
So then, what are we to make of the so-called hyperreals? The idea of the hyperreals is to extend the real line by adding in both infinitesimals and transfinite ordinals to the sequence of fixed, finite real numbers, so that (a) there are an infinite number of points, or positions, on the hyperreal line that somehow sit “between” each pair of successive reals on the line; further, these numbers are not real numbers but infinitesimals, each with its own fixed position on the hyperreal line, with the sequence of the infinitesimals “near” a particular real number getting “ever closer” to that real number, but never actually reaching it; and (b) there is a point on the hyperreal line that represents the totality of the natural numbers, i.e., a point that is the “highest” of the natural numbers, and we label the unit point just “beyond” this ω, and then proceed with the extension of the real line to ω+1, ω+2, … , 5.83ω, … , ω2, …, and similarly in the negative direction. Further, each of the ω numbers is supposed to be its own fixed hyperreal number (if it was not it could not have a place, or a point, of its own on the hyperreal line), so that the same pair of infinite sequences of infinitesimals that we suppose surround every real number also surround every ω number.57
There are so many flaws with these ideas. First, as we have discussed, the idea of ω is itself logically contradictory, because it is an attempt to finitize an infinity so that we may be able to treat this infinity in the same manner as we treat finite quantities, e.g., by adding 1 to it, or by dividing by it so that we may say that 1/ω = ε, and vice versa. These operations make no sense if performed on an infinity. Second, in trying to make all hyperreals that involve ω be fixed points on a line in the same manner that finite quantities may be fixed on the line, we ignore the fact that ω represents infinity, and thus the only way to treat such a “number” that is not logically contradictory is to see it as an always-moving, always-changing sequence of numbers, and thus as something that can never have a fixed place on any number line or in any linear number sequence. Third, it makes no sense to say that there is a “progression” of infinitesimals on either side of any given real number such that these progressions get ever closer to the real which they “surround,” but never actually reach it. If ε is such an infinitesimal, then by definition it is smaller than any positive number, and so since in order to avoid a logical contradiction it must always be changing, it is not a number, and therefore there is no “unit infinitesimal” that could serve as the “smallest” fixed infinitesimal quantity of which all the other infinitesimals in the progressions leading up to a given real number could be multiples. Furthermore, even with the regular real line, without the hyperreal extensions, one can magnify the line as many times as one likes, and no matter how many times one does this, an infinite number of points can always fit within the tiny magnified space, and these will all be real numbers. Also, as soon as we fix the position of an ε, no matter how small, so that it could actually be a number, and thus serve as a unit multiple for an ε sequence, it would become a real number and would cease to be an “infinitesimal.” There is, literally, no room for anything other than real numbers in any linear sequence of numbers, i.e., it is impossible for there to be an “extension” of the reals to include any other numbers in the linear sequence. Arbitrarily deciding that such an extension is possible, and drawing out on paper the “extension” of the real line to “include” the infinitesimals and transfinite ordinals, does not make it so.
For the sake of illustration, imagine a sequence of these infinitesimals that approaches a particular real number. But because it is a contradiction to say that any of these infinitesimals is fixed on the number line, then this entire sequence of infinitesimals will be forever shrinking. This means that no matter how many infinitesimals are in this sequence, the “gap” that would exist at the “halfway point” between one real number and its successive real number would not only exist, i.e., there would be a discontinuity between the two supposedly successive reals, but if we ever stopped adding infinitesimals to either of these sequences the gap would begin to grow ever wider as the sequence of infinitesimals on either side of it continued to shrink. The only way to stop this gap from growing would be to continue adding infinitesimals on both sides, and this adding of infinitesimals could never stop, because otherwise an ever-widening gap would form, contradicting the presumed continuity of the hyperreal line (aside from the fact that even if we kept adding infinitesimals in this way, since they would only be positions of zero length, then even this process could never create or provide continuity, to any degree, between the two successive reals, or between any two “successive” infinitesimals). Furthermore, it is stated that “the hyperreal numbers satisfy the transfer principle, a rigorous version of Leibniz's heuristic law of continuity.”58 With respect to the infinitesimals, the law of continuity states that “infinitesimals are expected to have the ‘same’ properties as appreciable numbers.”59 Note that it would be inaccurate, of course, to not put the word “same” in quotes in comparing the infinitesimals to “appreciable numbers,” i.e., numbers that actually do have fixed magnitudes. It is further said that “In 1955, Jerzy Łoś proved the transfer principle for any hyperreal number system. Its most common use is in Abraham Robinson's nonstandard analysis of the hyperreal numbers, where the transfer principle states that any sentence expressible in a certain formal language that is true of real numbers is also true of hyperreal numbers.”60 Of course, if one is careful to define the hyperreals so that nothing true about the reals is false in the context of the extension of the reals known as the hyperreals, then everything that is true about the reals will also be true about the superset of the reals known as the hyperreals. However, it should be noted that because the concept of an “infinitesimal” being equal to a fixed magnitude is logically contradictory, then any “proof” or “theorem” that claims to show that this can, in fact, be the case, or that depends on this being the case, will itself be flawed, and will depend, in one way or another, on the glossing over of the essential difference between the finite and the infinite, i.e., on the treating of a reasonably accurate – at least, for certain purposes which we may be interested in at the moment – approximation between these two things as if it were an identity.
Also, there is literally no place on a line to put the first transfinite ordinal ω in order to extend the real line that would not involve a contradiction. As soon as we place it at a fixed point on the line, it becomes clear that there could be a single unit of distance measured beyond this point, and then another, and then another – i.e., that it is a logically valid operation to take the natural numbers beyond this point. In fact, this is exactly what is done when we say that the point ω+1 is 1 unit beyond ω, ω+2 is 1 unit beyond ω+1, etc. But this is a contradiction because ω is supposed to be the “highest” of the natural numbers, i.e., it is supposed to be the case that at this point all the natural numbers are “taken,” so to speak, and cannot be used any further to count or mark off equal units of distance. It is more correct to say that, as ω is defined, at the ω point the line not only comes to a complete end, but also that literally nothing at all could ever extend beyond this point. If anything at all could extend beyond this point, including the real numbers themselves, space itself – if we even had the coherent ability to conceive that “there could be something beyond this point” or “there could be numbers beyond this point” – then it would be possible to extend the natural numbers beyond this point as well, which would then mean that the ω point was not, in fact, the absolute end of the natural numbers after all. The only valid way to use ω is the same way we typically use the symbol ∞, i.e., as meaning that which nothing can be greater than. As such, the only valid ω “point” on the real line is a point that is never reached, because ω represents the “highest” natural number, and since the natural numbers are infinite, and thus increase without bound, there is, in fact, no such thing as a “highest” one of them, and thus it makes no sense to say that ω could ever have a fixed point in a linear number sequence, no matter how far we extend the line or how many numbers we include. The belief that it is possible to have a fixed point in a linear number sequence for ω and for all other transfinite ordinals is an outgrowth of the familiarity we have with treating transfinite ordinals in set theory as if they were finite. If we are already used to adding and subtracting transfinite ordinals, taking the transfinite ordinal power of a finite number or another transfinite ordinal, creating infinite sequences of infinite ordinal “numbers” that get larger and larger; if we are already familiar with concepts such as “limit ordinal,” completed infinite sets, and different “levels” of infinity; then it is no great leap to conclude that it is also a valid idea to extend the number line not just beyond the “highest” natural number, but infinitely beyond this point. In fact, it is no more or less contradictory to specify a fixed point for ω as it is to specify a fixed point for ω1, the first uncountable ordinal, and for every uncountable ordinal after that. One may not be quite clear on exactly how this is to be done – after all, ω is just the next “unit” number beyond the “ultimate” natural number, while ω1 is supposed to be uncountably infinitely beyond ω – but however it is done, it must be done in a way that cannot possibly involve the natural numbers, because these are envisioned to be completed at the ω point. How is one supposed to move upward beyond the end of the natural numbers so that one is able to reach this higher level of infinity, this “uncountable” level of infinity? But this lack of clarity itself is a consequence of the logical error in assuming that there are different levels of infinity that in some way can relate to each other, and that each “level” of infinity can be treated as a finite thing for which it is meaningful in the first place to try to compare its magnitude or cardinality to that of another “level” of infinity. Trying to understand where to place ω and where to place ω1 on an infinite number line both fall prey to the same logical error; it is only in assuming that there are different levels of infinity to begin with that we see the one as somehow an easier problem to solve than the other. Once we understand the source of the confusion, both of these issues clear up with equal alacrity. We should note also that saying that ω+1 is created simply by taking the completed set of natural numbers, which ω is equal to, and adding this set representation of ω as another element to the set, in the same way that set theory defines each finite ordinal by adding the preceding finite ordinal’s set representation as the next element in the total list of finite ordinals up to that point and setting this new set equal to the given ordinal, does not solve the problem of how to extend the natural numbers beyond the ω point, because this argument erroneously assumes that this operation which is logically valid in the realm of the finite can be extended to the so-called transfinite. In other words, this argument assumes that it is possible to reach the ω point in the first place, in order to go beyond it, but actually this is impossible.
We are told, however, that the theory of hyperreals has been developed to a substantial extent by certain mathematicians, and has certain applications outside analysis, such as with hyperreal fields and rings in algebra, and in topology.61 But so has the theory of different levels of infinity in set theory,62 and we have seen how well this theory holds up to scrutiny. We are also told that the use of hyperreals in undergraduate calculus courses makes it easier for mathematics students to grasp the concept of a limit than does the δ-ε method,63 and that it can make certain proofs or constructions in analysis simpler, e.g., with the definition of the derivative using the concept of “st,” or the “standard part” of a hyper-real, i.e., the real number that is closest to a given hyperreal; among other redefinitions of familiar con-cepts in calculus and analysis using the hyperreals.64 But as with the real line itself, or the δ-ε definition of a limit, these methods can at best be practical tools that make certain practical tasks easier for the mathematician or the mathematics teacher. As always, we must be careful not to confuse the practical conceptual tools which we use with the structure of reality itself – these conceptual tools may be reasonably accurate representations of parts of reality or may help us solve problems within certain bounds of applicability, but outside these bounds any use of these practical conceptual tools will inevitably encounter flaws, errors, and contradictions.
There is also the concept of the “extended real line,”65 which is defined to be [-∞, ∞], i.e., the traditional real line (-∞, ∞) but “extended” so that it is closed, that is, with the infinity “endpoints” included, as if they were somehow suddenly made finite. Whatever the didactic value or mathematical convenience of such a construction, it should be clear at this point that a contradiction is involved here – the equating of the infinite with the finite – and that if we wish to understand foundational truths, rather than to at most make good approximations to the foundational truth, then if our thought and analysis is based in any way on this construction, the so-called extended real line, we will inevitably be involving ourselves in CH-style opaqueness and intractability, because this construction is logically flawed; if we wish, on the other hand, to use this concept in an approximational manner only, then perhaps there is a certain amount of practical value that may be garnered from this construction. The same argument applies to the “real projective line with a point of nullity” as described in “wheel theory.”66
In discussing adding infinitesimals to the reals and treating infinitesimals as if they were actual numbers, rather than at most useful conveniences, Potter says, “But if we take that course … and treat infinitesimals as real, we lose even the limited stability we obtained ... and have no reason not to posit a new level of objects which are infinitesimal relative to the non-standard field… . If we do this, we arrive at a conception of the continuum which is very different from, and far richer than, the Weierstrassian one. But adopting this conception would have radical consequences too for the set-theoretic reduc-tion we have been contemplating in this part of the book. For the proposal now under consideration is that we should conceive of the continuum as indefinitely divisible in much the same way as the hierarchy is indefinitely extensible, and it seems inevitable that if this idea is thought through it will eventually lead us to abandon the idea that the continuum is a set of points at all.”67 Here, Potter perceives that there is something not quite right, not quite sound, about the theory of infinitesimals as being actual numbers on an extended number line, and even hints at the underlying reason why this is the case. We should note first that the conception of the hyperreal line as being “far richer” than the “real” real line is no different from the conception of the transfinite and different levels of infinity making set theory as a whole “far richer” in structure than it would otherwise be; in both cases, the greater richness in structure is due to a logical error, and when this error is appropriately hidden from us through enough layers of indirection – not unlike the laundering of money – we obtain a feeling of justification in conflating two things that are fundamentally different, and treating them as equal – in the one case treating nothing as if it were something, and in the other case treating the infinite as if it were finite. If we are not bound to respect that these are logical errors, then of course all sorts of results may be obtained that we would otherwise not be able to obtain. Effectively, the belief that such results are definitive and logically valid is no different from wishful thinking or daydreaming, and springs from the same emotional source as these things. Potter then states that a consequence of the addition of infinitesimals, treated as actual numbers, to the real line is that the continuum is now indefinitely divisible, and thus indefinitely extensible from within, which makes it impossible to hold onto the idea that the reals ex-tended in this way can ever form a set, by which is implied a completed collection of things. The implicit assumption here is that reals by themselves are such a completed collection, and are therefore not indefinitely divisible; i.e., once we get “down” to the point of a particular real number then there is no further division to be had, as we are now at the fully atomic level of the real line. But with the addition of infinitesimals, i.e., “fixed” non-zero quantities that are nonetheless smaller than any other quantity that can be explicitly marked as a position on the line, the line is indefinitely divisible because no matter what there is always a smaller infinitesimal next to a particular real number than any infinitesimal we may care to “locate.” Also, as Potter states, if we allow for such an “extending from within” of the real line, there is no reason why we cannot extend in the same way from within the hyperreal line, and in this way continue such a process of “extending from within” down to as many levels as we like. Potter draws the conclusion from this that it becomes at best difficult to think of the continuum extend-ed in this way as a set at all, because a set is supposed to be a completed collection of fixed elements or quantities.
Potter is correct in that there is something amiss regarding the addition of infinitesimals as if they were numbers on an “extended” real line, but the reason for this is not that infinite or unending “extension from within” is possible in such an arrangement, but that infinitesimals by definition are not numbers, i.e., they are not fixed quantities, and so it is logically absurd to try to “locate” or “fix” a “particular” infinitesimal’s position on a number line in the same way that we do for an actual number. Infinitesimals can at most be a conceptual mathematical convenience, and can never be fixed points on any number line, because their definition precludes them being fixed at all. Potter makes general reference to this when he says that “the pattern in mathematics has always been that elements which start out as mere posits become accepted and end up being treated as real.”68 However, regarding the idea of indefinite divisibility, we must clarify certain things. First, we will say that with a correct understanding of infinity, as presented in this paper, the concept of indefinite divisibility of a particular part of the real line is no less logically valid or intuitively comprehensible than the indefinite extensibility of the natural numbers, or the reals. In his comment, Potter does not quite see this, first due to the fact that the idea of an infinitesimal “number” is logically contradictory, and so trying to understand the precise nature of the indefinite divisibility that is entailed by the presence of infinitesimals will always be an exercise in futility; and second (though here I am postulating a little) Potter, like most thinkers regarding set theory, likely views non-well-founded sets as somehow fundamentally different, or in any case notably different, than infinite well-founded sets, and the idea of infinite “divisibility from within” of the real line due to the addition of infinitesimals is very similar to the idea of an infinite regress within a particular element of a non-well-founded set, and so since the latter is somehow different or special, the former feels as though it might be also. But with a correct understanding of infinity, i.e., that the only logically valid conception of infinity is one that views infinity as countable, we can see that the infinite regresses of non-well-founded sets are perfectly understandable as expressions of countable infinity, no different from infinite well-founded sets. (See the more detailed discussion of non-well-founded sets in the section on them below in this paper.) Further, since the real numbers themselves, being fixed positions of zero length a particular distance from a reference position, also of zero length, can never add up to a non-zero, positive length, then if we are to treat these real numbers as representing fixed Euclidean distances from a fixed reference point we must conclude that there is literally no line at all that these positions build up to create, even though the positions are all in a linear sequence according to their relative magnitudes. Therefore, the problem of “indefinite divisibility” is not actually an issue, since if we build up the “real line” from just the real numbers themselves, we do not create anything at all which could be divided. The idea that this can even happen is due to the conflation of the finite with the infinite, and is thus logically invalid. Therefore, the real numbers lined up in a sequence according to their magnitudes is, within a given interval, an infinitely increasing collection of positions, and as such we may say that even in the absence of the addition of infinitesimals to this linear collection of points, the reals by themselves are indefinitely divisible, or, more appropriately, indefinitely accumulative. But this in itself does not prevent us from creating a set of the reals, because each real that is accumulated in this linear sequence is always a fixed point, and thus a finite entity, the precise type of thing which it is acceptable to collect into a set in the first place. It is therefore not true that through successive magnification we could eventually “reach” a point on the “continuum” that is no longer divisible and that also is directly next to the two points on either side of it so that the three points together create, however small, a non-zero, positive accumulation of length, and so that there are no gaps between the points. The correct way to view the real “line” is as an ever-increasing collection, which at any concrete step in the increase process is a finite collection, of zero-length positions that get ever closer to each other but never touch each other, and which as a whole never allow for any length accumulation. These fixed positions known as the real numbers are indeed atomic, in the sense that they are not further divisible; but it is incorrect to say that when we have “reached” the atomic scale we will be able to perceive actual continuity as a line. The idea of these points collectively accumulating to a continuous line is a useful convenience, a practical conceptual tool, no more. We can therefore see that the problem with the idea that infinitesimals could be numbers has nothing to do with the indefinite divisibility of the real line that this idea could supposedly create, but rather with the fact that the conception of a fixed infinitesimal point is logically contradictory, and thus inherently non-understandable.
Among set theorists, there are some who propose the idea that multiple versions of set theory, with mutually contradictory sets of axioms, are all correct, each in its own vaguely-defined “universe” in the “multiverse” of set theories. Such an idea is motivated partly by the fact that depending on the axioms one chooses to add to ZFC, CH can be shown to be true, or shown to be false, and there seems to be no way to sort out which one is the “correct” extended version of ZFC – not unlike the irreconcilability of contrasting religious viewpoints. It is, of course, also partly based on the idea from modern quantum mechanics of a superposition of states of a wave function, and the “multiverse” hypothesis that is associated with this concept. However, it is an act of denial to assume that contradictory statements or things can, in any way, coexist in the real world. The world is, and must be, logically self-consistent in its entirety.69 The multiverse of sets idea is nothing but an attempt by certain philosophers and set theorists to take what appears to be a respectable idea from the most revered of sciences – at least in our time – modern physics, and capitalize on a superficial similarity between the “multiverse” of superposed quantum states and the collection of mutually contradictory versions of set theory. It is thought that perhaps because so many decades have passed without any real progress in understanding CH or in reconciling the mutually contradictory versions of set theory, these mutual contradictions just may be the natural state of things. But this is to blind oneself to a logical contradiction out of the need to find a solution to an ongoing, difficult problem, as well as out of the frustration with not having found a solution yet. The persistence of opaqueness, in this case of the inability to reconcile multiple mutually contradictory sets of ideas that all seem equally correct, or at least whose incorrectness we consistently fail to find a way to prove, is not, and cannot be, the result of the fact that a logical contradiction exists in reality. Such persistence is always the result of a logical error in our own thinking. Instead of trying to find a way to make a logical contradiction logically valid, we need to realize that reality, all of reality, is, and must be, logically self-consistent, i.e., that a logical contradiction cannot exist, precisely because it is a logical contradiction. By locating the source of the logical errors in our thinking, the way to untangle these seemingly impossible knots, to forge through to the other side of these dark and seemingly impenetrable thickets of half-ideas, is rather remarkably laid out before us in short order. Clarity can only come from logical thinking. It can never come from assuming that a logical contradiction is not a logical contradiction.
There has been substantial debate over the past century on whether it is coherent to say that a “set,” which is supposed to be in some important sense a completed, and thus finite, thing, can contain an infinite number of elements. In fact, this debate also involves a conflation of the finite and the infinite, and its consistent lack of satisfactory resolution is due to this conflation. The argument that such a set is well-defined is bolstered by the fact that it is easy to recognize the pattern by which elements are added to the set, and thus we can see that no matter how many elements are added to one of these sets, the pattern will allow for as many more as we like. The naturals, for example, are built by the successor operation, the integers by adding 0 and mirroring each natural with its multiplicative inverse, the rationals by taking ratios of integers, the reals by combining the rationals and irrationals, and the complex numbers by combining the reals and imaginary numbers.70 In each case it is easy to see the pattern by which further elements are added to the set. It is easy, for example, to quantify over various infinite sets in first-order predicate logic, and this is precisely because we can clearly see that (a) each element in the set is finite, and (b) each set has a simple pattern by which new elements are generated and added to the set. Because of this clarity, it can seem to us that we have been able to entirely encompass these infinite sets in our thoughts about them, and we then proceed to treat them as if they were, in certain ways, finite, i.e., complete and fully circumscribed. But, in fact, we have not actually fully circumscribed, and can never fully circumscribe, all the elements in these sets, because the number of elements is infinite, and thus increases without bound. When we feel we have entirely encompassed one of these infinite sets, what we have actually entirely encompassed is the pattern itself that defines the set, because the pattern is finite – e.g., the pattern of the natural numbers is to start with 1 and add a 1 to this number to get the next number, and then this pattern can be repeated in sequence without end. Simple, and finite. Then, by use of this well-understood, finite pattern we may proceed to make statements about all the natural numbers, because they all conform to this pattern, and so if a statement is true about the pattern itself, which, recall, represents the entirety of the numbers that the pattern can produce, it must be true about each number in the pattern – mathematical induction is an expression of this. Mathematical induction is a well-defined operation that does not contain any logical contradiction precisely because the pattern of the set of natural numbers is finite. The ability to think of the natural numbers, or any of these infinite sets, in terms of the finite patterns which produced them is useful in a wide variety of mathematics. At this point, there is no logical error in our thinking.
The problem comes when we try to treat this finite pattern that defines one of these sets as if it were the infinite “collection” of elements in the set itself. We are so used to being able to “quantify” over the naturals, the rationals, etc., that we do not notice that we have started to think of each of these sets of numbers as able to be completed, or fully bounded, or finished. The reality is that because each of these sets is defined by a pattern of generation, then it contains within its definition an infinity, and as such the number of elements in each of these sets increases without bound. This means that it is literally impossible to “collect” all of them together into a finite, bounded collection that can be manipulated as a whole or as a unit. We may “quantify” over the entire infinite set, but when we do this we are not treating the entire infinite set as a bounded whole; we are, rather, treating each element in the set individually, and the idea of quantifying over “all” the naturals, rationals, etc., is only shorthand for the successive individual operations made in sequence on each of the numbers in the set; that is, the idea of “quantifying over the entirety of an infinite set” is a practical conceptual tool, a convenience, to make analysis and proof easier by the recognition of the pattern by which all elements in a given set are constructed; it does not allow us to feel justified in the belief that we have been able to entirely encompass all the elements of this infinite set and thus “finish” the process of collecting them. Further, it is important to emphasize that the act of “quantifying” over an infinite set can never be completed – since each element in the set is treated individually in the actual tasks or operations which are represented by the sentential logic, and since the number of elements in the set is infinite, then the process of treating these elements, i.e., quantifying over them, will never be finished. We may legitimately draw general conclusions about all the elements in the set based on the recognition of the pattern by which the elements are constructed; but we are never justified in saying that we have actually quantified over all the set’s elements. This is the essential difference, and as with, e.g., the concept of an infinite decimal sequence approaching a finite limit point, we are often so accustomed to thinking of the two as the same thing that it can be difficult at first to recognize, or to admit, that there is any nontrivial difference between them. But if we are to have a clear and full picture of what we are trying to understand, it is crucial to recognize all nontrivial differences between thing we view as similar, as well as all nontrivial similarities between things we view as different. In the case of the various infinite sets of numbers, the pattern that defines the set is finite and thus circumscribable, but the number of elements that can be produced by the pattern is infinite, and thus not circumscribable. In conflating these two, we have created a debate where there is a certain level of validity in each side’s viewpoint, but where at the same time the different sides seem to be logically irreconcilable. Any time this type of situation arises, we must look for a logical error in our thinking as the source of this impossible state of affairs. The different sides of a debate cannot both (or all) be right if the sides take contradictory views on the subject. But debates such as this one can persist for as long as they do precisely because both sides are right at the same time.
The Cantor set is defined by starting with the closed unit interval, removing the middle-third as an open interval, and then repeating this algorithm, this pattern, ad infinitum on each of the remaining segments. “At infinity,” the total length removed is 1, i.e., everything, at least in terms of Euclidean length, is removed, and so one may think that after the process is finished there is nothing left. But in fact, since this segment removal process is infinite, it can never finish. We will not discuss every idea that has been considered in relation to the Cantor set. However, we will discuss a “proof” of the set’s uncountability.71 We are told that “it can be shown that there are as many points left behind in this process as there were to begin with, and that therefore, the Cantor set is uncountable.” We are told that it can be shown that the mapping of the Cantor set to the closed interval [0, 1] is surjective, meaning every element, every number, in the interval [0, 1] is mapped to by at least one element in the Cantor set. But since the Cantor set is clearly a subset of the interval [0, 1], then the Cantor set cannot be greater than the interval [0, 1] in number of elements. Therefore, by the squeezing property, the Cantor set must be equal to the interval [0, 1] in number of elements. But since the cardinality of this interval is uncountable, the Cantor set itself must also be uncountable.
We have discussed in this paper the logical contradiction of the idea that there are multiple levels of infinity. In fact, the “proof” that the Cantor set is uncountable resorts to the same conflation of the finite and the infinite as the diagonal argument does, i.e., it treats infinite sequences as if they were equal to finite magnitudes, rather than as what they are, viz., sequences of ever-changing magnitudes. The proof can be read in the Wikipedia article, but it starts by considering the endpoints of the intervals that remain after the “middle-third” is removed from any segment. These numbers are rational numbers that do not contain the digit 1 in their ternary expansions and whose ternary expansions end in either all 0s or all 2s. All other numbers in the Cantor set also do not contain the digit 1 in their ternary expansions, but these expansions do not end in all 0s or all 2s, instead ending in non-terminating combinations of these numbers.
The problem with the argument of the Cantor set’s uncountability is that it conflates the finite with the infinite, i.e., it treats these infinite ternary decimal expansions as if they were the fixed magnitudes that are their real number limit points. But because they are infinite decimal expansions, they can only ever approach their limit points; they can never actually reach them. Furthermore, it is also incorrect to equate the two because the infinite decimal expansions are always changing, while the limit points are fixed; and in order to equate two magnitudes, i.e., for this equating to be meaningful, both of the magnitudes being equated must be fixed. It is not a coincidence that we are told that the “set of end-points [in the Cantor set] makes up a countably infinite set.”72 (Italics mine.) The endpoints of the remaining intervals are not the only numbers in the Cantor set. But one quality the endpoints clearly have is that they are all fixed points, i.e., they are numbers, i.e., fixed magnitudes, and so it is clear that they can be lined up one-to-one with the natural numbers; and since the number of these endpoints never stops increasing, because the process of removing middle-thirds never finishes, it makes sense to say that they can keep being lined up one-to-one with the naturals for as large a number of endpoints as we choose to accumulate.
But the reason that the Cantor set is said to go beyond this, i.e., to be uncountable, is, as stated, that “the numbers in [the Cantor set] which are not endpoints also have only 0s and 2s in their ternary representation, but they cannot end in an infinite repetition of the digit 0, nor of the digit 2, because then [they] would be [endpoints].”73 In other words, the numbers in the Cantor set that are not endpoints are all represented by non-terminating sequences of digits. As a result of this, in their decimal representations they are not numbers at all, because no infinite decimal sequence can ever be equal to its finite limit point. Therefore, even when we add these numbers that are not endpoints to the growing list of numbers that we call the Cantor set, the only thing we may do that is not logically contradictory is to add the limit point itself – which is of fixed magnitude and therefore can rightly be called a number – rather than to add the imperfect decimal representation of the limit point, which, we may recall, itself can never be a complete or finished collection of digits, because the number of digits in the decimal representation is infinite. And, therefore, since we are only allowed to add numbers to the Cantor set, and numbers are always fixed values, i.e., in the case of the Cantor set they are always either endpoints, which it is clear are fixed points on the line, or the limit points of non-terminating decimal sequences, which are points that are not endpoints and for which it is clear are also fixed points, and since it is clear that for each such number added to the Cantor set we may increase our index sequence, i.e., the sequence of natural numbers, by 1, and since the sequence of natural numbers is infinite and thus never ends, we conclude that the Cantor set is, in fact, countable, not uncountable. Furthermore, we should take this opportunity to remember that because the number of elements in the Cantor set increases without bound, since the process of segment removal is never finished, then it is impossible to have a Cantor “set” that is completed or finished; to assume this is possible is to fall prey to the same conflation of the finite and the infinite that makes us think that the naturals, reals, rationals, etc., can be considered completed or finished collections just because we can clearly understand the pattern by which new numbers in the set can be forever generated. The Cantor set is produced by an easily-understood pattern, and this combined with our desire to tame the infinite makes us draw the illogical conclusion that we can, in certain important ways, build or create the Cantor set in its entirety, when actually all we can do is keep adding more and more elements to it without bound by continuing to apply the Cantor set pattern over and over. Also, even though “at infinity” the entire Euclidean length is removed by the Cantor set algorithm, we may say that (a) in reality the entire Euclidean length is not removed, and cannot be removed, because this would be equivalent to completing or finitizing infinity, and thus is a contradiction – at most, we may continue removing middle-thirds as long as we like; and (b) this serves as an illustration of the fact that points are zero-length, and as such we may accumulate as many of them as we like, and the sum total of their linear aggregate, whether they are placed “right next” to each other, which would mean they are the same point, or with gaps of empty space of various Euclidean distances between them, would still always be exactly 0. In other words, an ever-increasing accumulation of Cantor set points which result from continuing to remove middle-thirds would never contribute any Euclidean length to the resulting Cantor set. The standard argument concludes that the set of endpoints in the Cantor set is countable, which means the standard argument agrees that the set of endpoints measures 0 length. But we should note that the argument which concludes that the entire Cantor set is countable is in agreement with the geometric sum which says that the entire Euclidean length removal after “all” middle-thirds have been removed is 1, since, as is agreed by standard set theory, any countable subset of the real line has measure 0. We should just note, again, that because the process of removing middle-thirds is infinite, and thus never ends, the entire Cantor set can never exist alone in the unit interval – any process by which we imagine all such middle-thirds may be removed, particularly if we imagine them all being removed at once, instead of in succession, is an attempt to finitize the infinite, by removing an infinite number of segments of [0, 1] in a finite amount of time, and this is impossible. But the points that make up the Cantor set, being countable, exist within [0, 1] – though, again, never as a completed or finished collection of points, but only as an ever-accumulating collection of points – and, as is the case for all of the reals, both in this interval and in their entirety, the Cantor set points have, and must have, in their linear aggregate, a total measure of 0. In fact, the idea that the entire length removed from the unit interval by the Cantor set algorithm is 1 contradicts the conclusion that the Cantor set is uncountable, because one of the differences between countable and uncountable sets is supposed to be that while countable sets have measure 0, uncountable sets have positive measure, which then translates into a non-zero, positive Euclidean length accumulation on the real line.
Another way to look at the standard argument for the Cantor set’s uncountability is that we can list ellipsized approximations of the infinite decimal sequences which are erroneously equated with the actual Cantor set elements (which, recall, are numbers, and thus fixed magnitudes) that are not endpoints in the same way we did in the diagonal argument in the previous part of this paper, and no matter how many such sequences we add to the list, we can always create a sequence of numbers, per the diagonal procedure, that is not the same as any of the existing sequences in the list. But what we cannot do is create an infinite list of these infinite decimal sequences, and then take the diagonal of it with the result being a number that is not in the list, for the same reasons that this cannot be done in the diagonal argument: (a) it is impossible to have a completed infinite collection of elements, (b) the process of the taking of the diagonal would never complete, and so the “end result” of this process could never be a number whose magnitude could be compared with that of another number, i.e., the process of taking the diagonal of such a list is a process of perpetual change, and (c) the infinite sequences of digits that are the elements in the list are not numbers at all, because each one is an always-changing magnitude. In other words, if this argument does not work to prove that the set of reals in [0, 1] is uncountable, then it also does not work to prove that any set that has the same number of elements as the reals in [0, 1] is uncountable. Once again, after we have recognized that we logically erred in conflating the finite with the infinite, the opaqueness clears, and the seeming paradoxes that this conflation produces, such as the idea that even though a collection of numbers is less than another in magnitude, it can somehow also be more than the other collection in magnitude because a mapping can be found from the first set to the second set that is surjective but not injective, are shown to be just that, paradoxes,74 i.e., things that are logically contradictory, and that, therefore, cannot exist or be true.
It is not enough to say that results such as there being different “levels” of infinity or the idea that the Cantor set is uncountable are simply “counterintuitive but true,” and that we do not understand these results as clearly as we would like to only because of limitations, weaknesses, frailties, etc., in the human mind, i.e., because of human psychological and emotional shortcomings that can impede our full understanding of things, or because we are just not thinking about the results in the “right way.” This is to take the easy way out. Such a conception absolves us of having to explain the seeming paradoxes and contradictions. It is effectively no different from saying that something is the way it is because “God made it that way,” and depending on our particular emotional state and vested emotional interests, it may give us an excuse to not have to dig deep enough to find out that our tower in the sky, on whose peak we stand, is in actuality a flimsy house of cards whose precarious condition we never notice because all we ever do is look up. We must learn to be more humble, to look in all directions instead of just one; in doing so, we become wiser, and thus more aware of our own limitations, but we also find a great deal more of the truth we seek.
It has been shown that √2 is irrational by showing that it cannot be a ratio of integers, which is the definition of an irrational number. The proof is easily understood. The only comment here is that we must remember to distinguish between an infinite decimal expansion and the finite limit point to which it approaches. In writing 1.41421356…, we can never write a fixed magnitude that is equal to √2. This sequence of digits is unending and therefore represents an infinite sequence of changing magnitudes. But √2 is itself still a fixed, finite number and can thus meaningfully correspond to a fixed Euclidean distance, such as the hypotenuse of a right triangle with sides a and b equal to 1. We may conflate the two, the fixed Euclidean distance and the infinite decimal sequence, for certain practical purposes, so that the one is as close an approximation as we like to the other, but we should always remember that there is an essential difference between them, and that if we take things too far with this practical conflation we will, sooner or later, end up producing paradoxical results. Once again, conflation of two different things based on certain similarities between them can be a useful guide for us in understanding and thinking about the world. But conflation of two different things will always have its boundaries and breaking points, and as long as we continue to try to expand our understanding these boundaries and breaking points will eventually be encountered.
Point-free geometry can be seen as an attempt at overcoming the logical contradiction inherent in the conception that it is possible to have entities called points, of any quantity, which have zero dimension but which can somehow be placed next to each other in a way that produces a positive measure such as length, area, or volume.75 Instead of building up a space of some kind by collecting together points, we avoid explicitly mentioning points by talking about “regions” and “parts” instead. We say, for example, that neither “atomic regions,” i.e., regions that cannot be broken down further, nor “universal regions,” i.e., regions that contain everything, exist, so that the basic units of point-free geometry are regions that are parts of other regions and regions that have other regions as parts. We might say, for example, that a space that is made up of regions is continuous if, for every two regions A and B where A is a proper part of B, there is always a larger proper part C of B that entirely contains A, no matter how close A is to being equal to B. However, we get into murky territory when we start discussing what it is to be a boundary of a region or a part, because boundaries can, for example, be one-dimensional, as is the boundary of a closed area in the Cartesian plane. Is it possible for there to be such a thing as boundaries of regions or parts without running afoul of the initial assumption that we are not supposed to use the concept of points in point-free geometry? After all, how could a boundary curve be defined analytically other than as a sequence of points? Or perhaps we can get away with defining a “boundary” as that finite location which a region approaches but never touches. But even this definition is problematic, because it uses the concept of a finite limiting curve that forms the boundary of the region, even if the region is defined in such a way that it never actually touches the curve; and thus, indirectly, the definition uses the concept of a point, in the form of the sequence of points that make up the limiting boundary curve. Further, this definition conflates the finite with the infinite, and is logically flawed as a result, because it implies that the region is both static or finished, and at the same time ever-growing and thus ever-changing, i.e., this definition conflates the finite with the infinite in the same way that equating an infinite decimal sequence with its finite limit point does.
But one might try to get around this difficulty by saying that since there is no largest region (by definition), then before any “limiting boundary curve” is reached, a given region just becomes or transitions into a surrounding, larger region. But this is to negate the concept of region entirely, which is defined solely by its boundary. One may also define the boundary curve itself in the same way that one defines the interior of the boundary, by saying that it consists of “lengths” and “parts of lengths” such that the curve never gets down to the individual point level, with the variation that the “universal” length is the entire boundary curve of the region, so that universals in this case exist; but this would be to add a new element to the founding components of point-free geometry, since such a definition is (to my knowledge) not already included in point-free geometry. It would thus appear that point-free geometry as currently defined cannot be entirely point-free.
Even the definition of the space in question by saying that each region is made up of smaller regions and that this process can proceed to smaller and smaller regions as far as we like implicitly, if not explicitly, uses the concept of a point, viz., the limiting point of this infinite progression. But because this is an infinite progression of smaller and smaller regions of positive magnitude, the limit point is never reached, so that if we were to examine the regions at any point in this downward progression, we would always find that they had non-zero, positive magnitude (e.g., non-zero area in the Cartesian plane). This is the same as the δ-ε definition of a limit, where no matter how small an ε we choose, we can choose a δ such that if x is within δ of c then f(x) is within ε of L, without ever actually reaching L. Since the sizes of the regions can never reach the limiting point, then this part of the definition of point-free geometry effectively overcomes the explicit use of points, instead saying that the space in question is built up out of regions which are defined to already have non-zero, positive magnitude. And because we can continue splitting regions into parts as long as we like, we can split the original region into finer and finer parts that all approach, but never reach, “regions” of zero magnitude. To think that such splitting could ever actually reach the stage of “regions” of zero magnitude, i.e., of a collection of nothing but points, is more readily seen in this case to be absurd – specifically, to be a conflation of the finite with the infinite, and thus to be illogical. But as we have seen, such a conflation in other contexts can be more difficult to detect, and often goes undetected or partially undetected for many years or decades.
Whitehead’s point-free geometry attempts to avoid conflating the finite with the infinite by avoiding defining a space as a collection of points of zero dimension. But it is unclear whether this way of defining a space can produce better mathematical results than a sufficiently good approximation in standard point-based geometry that glosses over the conflation of the finite with the infinite. We are told that “point-free geometry was first formulated in Whitehead (1919, 1920), not as a theory of geometry or of spacetime, but of ‘events’ and of an ‘extension relation’ between events. Whitehead's purposes were as much philosophical as scientific and mathematical,”76 so this question may or may not have been relevant to Whitehead himself. But we may still look at point-free geometry as an attempt to locate and eradicate logical errors in our founding assumptions, and as such it is an expression of the overall philosophical and scientific effort to uncover the underlying truth about the world, as well as an expression of the effort to break the habit that we so often subconsciously keep walking back into of relying too heavily on familiar or comfortable concepts.
There are different formulations of the Banach-Tarski theorem, but they all basically state that a shape of a given volume can be disassembled in certain ways and then reassembled without any reshaping or stretching of parts in a way that produces a net increase in volume – for example, one unit sphere can be disassembled and reassembled into two unit spheres.77 But since the volume of, e.g., a unit sphere is a fixed quantity, how is it possible to take apart and reassemble it in a way that increases its volume without adding new or stretched pieces to the collection of parts that are reassembled?
It should not be surprising that the concept of an uncountable set is crucial to this paradoxical volume-increasing operation. In fact, we are told that “unlike most theorems in geometry, the mathematical proof of this result depends on the choice of axioms for set theory in a critical way. It can be proven using the axiom of choice, which allows for the construction of non-measurable sets, i.e., collections of points that do not have a volume in the ordinary sense, and whose construction requires an uncountable number of choices.”78 (Italics mine.) We will not discuss the proof in detail. However, just based on this quote we can see that the “proof” that a sphere can be doubled in volume without adding or reshaping any pieces just by the appropriate decomposition and reassembling conflates the finite with the infinite. The axiom of choice is used to choose an uncountable number of points of the unit sphere, and, in particular, these choices are made in such a way that the resulting “completed” set of an uncountably infinite number of points is non-measurable, i.e., it cannot be meaningfully assigned a Lebesgue measure, that is, a normal measure of Euclidean distance, area, volume, or magnitude. Of course this must be the case in order to produce the paradoxical result, because if the particular decomposition of the sphere that we chose was restricted so that it only produced Lebesgue-measurable pieces, no matter how small these pieces ended up being, then without stretching or reshaping the pieces it would, of course, be impossible to reassemble them into any volume that was not exactly equal to that of the original sphere. Thus, at least one of the “pieces” into which the original unit sphere is decomposed must be non-measurable; furthermore, this non-measurable piece must be uncountable, because it is clear that if we choose a countable number of points to make up this piece, its measure will be zero, and so such a piece is not of any use in a reassembly process that is supposed to increase the total volume of the sphere that was decomposed.
But is it even logically meaningful to have a collection of points that is non-measurable and yet at the same time can in any way represent a non-zero, positive magnitude when taken together? As we discussed in a previous section in the context of the real line, no matter how many points we place next to each other, because these points are of zero dimension we will always end up with exactly the zero measure with which we started. And it is no different with arranging points in order to try to create a two-dimensional surface or a three-dimensional solid that is embedded in a three-dimensional space. No matter how many points are arranged together, the end result, after as many iterations of the process of adding yet another point as we care to make, will always be zero surface area, zero volume. So, by ensuring that the collection of points which we create via the axiom of choice is non-measurable, we avoid having to face the impossibility of actually disassembling and reassembling a real sphere, either physical or conceptual – i.e., a sphere which does not contain any logical contradiction in its definition or construction – into two spheres each of which is the same size as the original. But in ensuring that this collection is non-measurable, we have completely negated the meaning of volume,79 since all volumes in Euclidean space, no matter how small, are always Lebesgue measurable, and thus we have not actually helped matters in the effort to try to paradoxically increase the volume of a sphere; all we have done in creating this infinite, non-measurable set is conflate the finite with the infinite, even assuming the set is only countably infinite, and on the basis of this flawed but familiar and comfortable conflation, we proceed to conclude that it is logically meaningful to say that a non-measurable set can actually have a volume, in any sense. But of course a countable number of elements in this non-measurable set can easily be seen to have zero volume, because it is easy to understand that placing points next to each other never produces, no matter how many points we add, any volume greater than zero. Therefore, we must reach into the realm of “uncountability” in order to increase this volume beyond zero, just as with our definition of measure from earlier as always being zero for any at most countable set, with the implication that if a set has non-zero measure it must be uncountable. In the same manner, we may contemplate the idea that while an at most countable collection of points is of zero volume, an uncountable collection of such points might just be able to have non-zero, positive volume. This idea is reinforced by the fact that we are already familiar with the idea that there are different “levels” of infinity and with the supposed definitive validity of the diagonal argument, and we are so inured to the process of glossing over the conflation of the finite with the infinite in such ideas that we do not see, or do not fully see, the significance of the logical error which we have glossed over in order to produce our varied and wondrous results. In the context of these ideas which are already based on the conflation of the finite and the infinite, of course it presumably should be possible to produce paradoxical results, i.e., to “prove” that such results are true. But if the basic assumptions on which a proof is based are flawed, then the theorem that is proved is not a statement that says anything about reality; at most, it is a statement that says that a logically impossible result can follow from a logically impossible premise – but this is something we already knew. Such a result is not a truth about the world, or about the world’s rational structure; it is an example of a pathological result that is based on an implicitly accepted logical error; once this error is uncovered and the appropriate corrections are made, the supposedly “proven” result vanishes. In the case of the Banach-Tarski paradox, once we realize that there is no such thing as multiple levels of infinity; that it is impossible to collect an infinite number of elements into a completed collection or set; that a decomposition of a body with positive Euclidean measure or magnitude can never get down to the place where we are finally at points, since at the level of points we are no longer taking any volume away, and so the decomposition cannot proceed further unless we start again taking away positive Lebesgue measures of volume; that no matter how many points we aggregate into a set, they can always be mapped one-to-one with the natural numbers, and that it is not only impossible to go “beyond” the natural numbers to eventually reach “uncountable” numbers in order to produce an “uncountable” set, but that, no matter how big we make the set, going “beyond” the natural numbers will never be needed in order to continue keeping track of the number of elements in the set; that no matter how many points we collect together into a set they can never add up to a Euclidean magnitude greater than zero, and so such a set, no matter how big, can never make any positive contribution, no matter how small, to the volume of anything – once we realize these things, the seeming “truth” of the paradox, of this conclusion or idea that seems to defy logic, no longer mystifies, because it has now become clear that since this result does defy the logically self-consistent structure of an inherently rational world, it is, as one would reasonably expect, an impossible result.
It can be a fun thing to show to one’s mathematical peers that one has done or proven the impossible. It is human nature to desire to do this. By doing this we stand out, we can make a name for ourselves, we can increase our chances of making a mark in history. But such desire can make it harder to recognize any logical flaw that might be latent in the thinking which led to these remarkable conclusions. We are disincentivized by our psyches to go looking for errors and problems, because these strokes of good fortune are so rare and difficult to come by, and we do not wish to risk upsetting the happy, but precarious, balance thus obtained. Ultimately, the human search is not for truth, but for survival. For the average person truth only comes into play in a narrow, practical sense in the context of the day-to-day need to navigate the world in order to survive within it. But for a few, the search for truth takes on a greater role in the overall search for survival. For such individuals, for whom an accurate understanding of the world’s foundations is of disproportionately high priority, it is important to be able to understand the overlap in our minds between the desire for truth and the desire for survival, and become practiced at teasing these two apart at the points where they differ. Otherwise, we will never be able to fully achieve our goal of understanding the world. The desire for truth and the desire for survival often overlap, but not always. It is in these latter cases, especially ones far removed from any immediate or near-term practical needs, that we can often afford to be fanciful in our thinking; these cases, therefore, can be enticing opportunities to satisfy, in a conceptual way, our need for survival, which in general often feeds on false but emotionally comforting ideas and beliefs, at the expense of our understanding of the truth, which is often emotionally displeasing or distressing. There is nothing inherently wrong with doing this, and, in fact, false but emotionally pleasing ideas and beliefs can often make a person happier and more content with their life than would a full acknowledgment of the truth. But, again, truth is truth; we do not have to be happy with an idea for it to be true. Anyone for whom the quest for truth is truly paramount must eventually come to terms with any logical error in their thinking, or they will never be able to fully accomplish their goal.
Potter states, “The Banach/Tarski theorem has sometimes been used in an attempt to refute the axiom of choice: the conclusion of the theorem is intuitively false, it is said, and therefore the axiom of choice cannot be true. In order to use it this way, though, we would need to have an intuitive argument not depending on the concept of area for disbelieving in the possibility of the decomposition mentioned in the theorem, and it is by no means clear that such an argument exists… . [T]he Banach/Tarski theorem has led some mathematicians to speculate on the idea of abandoning the axiom of choice and put-ting in its place an axiom which ensures that every set is measurable and hence rules out the decompositions of the sphere which they find paradoxical.”80 But we have seen that there is a genuine paradox, i.e., a logical flaw, in this decomposition, because in using the full axiom of choice, or full AC, which extends the axiom of countable choice to the realm of uncountable infinity, we are assuming that it is possible to create an uncountable set of points that makes up the non-measurable part of the decomposition. But since it is impossible to create such a set, because the concept of uncountable infinity is logically flawed, and because it is impossible to complete an infinite set anyway, so that the “completed” infinite set can be a fixed component or piece of the volume which can be added to the remaining pieces during the reassembly process, even if the infinite set is countable, then actually any logically valid decomposition of the unit sphere (a) could only be done by the use of non-zero, positive chunks of volume, however small, and (b) could only ever be reassembled into a single unit sphere. With regard to AC, what the Banach-Tarski paradox points to is not that AC is completely wrong, but that the extension of the axiom of countable choice to the realm of uncountable infinity is wrong, and thus that the full AC is logically flawed, while nothing is said by the paradox regarding the more restrictive axiom of countable choice. This is the intuitive argument which is not dependent on the concept of area (or volume) that Potter seeks but does not know how to find. Further, Potter cannot find this argument because he is still in the grip of the logically flawed belief that the uncountably infinite exists, which belief bars avenues of thought that would bring clarity, and clouds his philosophical and mathematical judgment.
Goodstein sequences are sequences of natural numbers under a recursive operation that, based on rather small and simple initial conditions, nonetheless show an extremely rapid rate of increase, except for the first three of these sequences based on the first three natural numbers.81 Potter gives an example in which if we start a Goodstein sequence with the number 51, the very next element in the sequence is on the order of 1013, and by only the seventh iteration of the recursion operation the element’s size is on the order of 1015,151,337, a rapid increase.82 There is a theorem in set theory which says that, just like the Goodstein sequences that begin with 1, 2, and 3, which terminate, i.e., reach 0, after 2, 4, and 6 steps, respectively, every Goodstein sequence eventually terminates. The proof makes use of ω, the infinite ordinal that is equated with the totality of the natural numbers, and so a question arises as to whether, in light of what has been said in this paper, the Goodstein theorem and its proof can be considered valid.
At each step in the Goodstein sequence, the natural number produced at that step is the sum of one or more terms of a mathematical expression, and at the nth step this mathematical expression is written in what is called complete normal form (CNF) to base n+1. Sometimes the immediate result of an iteration of the sequence is the number in CNF, and sometimes it is not; in the latter case, the format of the expression representing the number must be modified so that it is written in CNF before the next iteration of the sequence is made. The proof consists of creating a parallel sequence to the Goodstein sequence – a one-to-one mapping – that starts at the “other end” of the Goodstein sequence by taking the first element in a given Goodstein sequence, writing it in CNF to base 2, and replacing each instance of 2 with ω; and then for each successive step replacing ω with n+1 again, performing the normal Goodstein algorithm, including rewriting the result in CNF if necessary, and then replacing every instance of n+1 in the new step with ω. The ω expressions are compared across steps, and the argument concludes that the parallel sequence is strictly decreasing and eventually reaches 0, and so the Goodstein sequence itself, corresponding as it does to the parallel sequence, must eventually reach 0 also, regardless of which natural number starts the Goodstein sequence. Note that the parallel sequence is also called the Goodstein ordinal sequence, or just the ordinal sequence, which is more descriptive of the way the sequence is used in the proof, and so we will use this term for the parallel sequence going forward. Potter gives two examples on p. 216 of his book. For the number 3, we have the following:
γ(3, 1) = ω + 1
γ(3, 2) = ω
γ(3, 3) = 3
γ(3, 4) = 2
γ(3, 5) = 1
γ(3, 6) = 0
And for the number 51, the following:
γ(51, 1) = ωωω+1 + ωωω + ω + 1
γ(51, 2) = ωωω+1 + ωωω + ω
γ(51, 3) = ωωω+1 + ωωω + 3
γ(51, 4) = ωωω+1 + ωωω + 2
γ(51, 5) = ωωω+1 + ωωω + 1
γ(51, 6) = ωωω+1 + ωωω
⋮
We are told that in these examples we can “observe that the Goodstein ordinal sequences are strictly decreasing from the very start.”83 But, though at first glance this would appear to be true, there still seems to be something amiss about this downward progression of numbers, and it comes down to the use of the ω symbol, which represents infinity. The expressions in the Goodstein ordinal sequences purport to arithmetically manipulate infinite, and thus always-changing, entities as if they were finite, i.e., fixed, entities, and thus as if they were numbers; therefore, the Goodstein argument conflates the finite with the infinite and so relies on a logical error. Such a sequence of expressions could only conceivably represent a strictly decreasing sequence of numbers if the ω symbols in the expressions were made to represent fixed, and thus finite, quantities, but this is clearly not what ω is meant to represent in set-theoretical arguments. If, on the other hand, the ω symbols in the Goodstein argument are meant to represent infinity, as is implied by the fact that the ω symbol was chosen for the argument, then it makes no sense to subtract one, or any finite number, from the numerical value at each step in the sequence and then say that the result is a reduction in magnitude compared to the ordinal number at the previous step, because subtracting one, or any finite number, from infinity to produce a smaller number is nonsensical, i.e., this process could not reduce the previous ordinal number at all: what is being subtracted from is infinity, not a finite number that can be reduced, and so if we interpret ω as infinity, then we cannot conclude that any Goodstein ordinal sequence strictly decreases, since the concept “decrease” has no meaning unless both minuend and subtrahend are fixed, i.e., finite.
By using the ω symbol and the concept of infinity to which it refers, the Goodstein argument conflates the finite with the infinite, and in the process confuses matters, especially given that the argument is seen as a paragon of a deep, beautiful, profound, or elegant proof, viz., a proof that is simple to construct yet seems to prove much more than its simplicity would seem to allow; and this elegance makes it harder to see the flaws in the proof, because we do not want to relinquish the elegance, which is always rare and hard-won. Also, if, in order to avoid the contradiction inherent in using ω to mean infinity while at the same time trying to create meaningful arithmetic expressions using it, we treat ω as a fixed, finite quantity that remains the same across steps (which is implied to be the case by the fact that the same symbol, ω, is used across steps), then without any independent information about the behavior or ultimate fate of the Goodstein sequence, we do not, in fact, have enough information to say that the ordinal sequence strictly decreases. This is due to the behavior of the ordinal sequence under the condition that n+1 at every step be replaced by the same number, say, 1,000,000, i.e., that the number replacing ω at every step be constant across steps. The behavior is that if the number is large enough, we will see a strict decrease from the start, but only to within the vicinity of the point where the constant chosen begins to be matched in magnitude by n+1, and as the right-most term dwindles to 0 by being reduced by 1 at each step and then the next-left term is broken out into new right-bound terms, the right-most term is doubled from what it was before, but the term that was broken out is reduced by the same factor, since ω represents a constant value across steps. As this process continues, the right-most term continues to double the value the previous right-most term was at the last time the next-left term had to be broken out, while at the same time the term that is broken out continues to be reduced by the same factor. Beyond a certain point, the reduction by a constant factor is more than compensated for by the doubling combined with the additional broken out right-bound terms, and we then see an increase, not a decrease, from one term to the next in the ordinal sequence. If there is no independent information about the nature and behavior of the corresponding Goodstein sequence, then we do not have enough information to say whether there is a constant value that ω could be that would ensure that the reduction by a constant factor always ensures a strict decrease across steps in the ordinal sequence, and thus ensures that the ordinal sequence reaches 0. If we chose a larger value for our constant, say, 1068, then it would take a longer time for n+1 to get to within the vicinity of matching our constant, but without any independent information about that nature and behavior of the original Goodstein sequence, we cannot say that the ordinal sequence will not reach this point, and then go beyond it, with the result that it once again would not be strictly decreasing, which, in turn, would mean that we could not use the “strictly decreasing” argument to say that the Goodstein sequence eventually terminates. What is needed is an independent argument that says that there is a point in the Goodstein sequence where there is no longer any instance of n+1 at step n, at which point the net result of the Goodstein algorithm at each step is to reduce this finite number by 1, which would then mean that the Goodstein sequence reaches 0 after a finite number of steps. With such an argument in our back pocket, we could say, without even knowing what the highest n+1 value is for a given Goodstein sequence, that if we take our constant to be that particular number then the ordinal sequence is strictly decreasing and thus will eventually reach 0, because the sum of the duplication of the value in the right-most term and the values of the remaining right-bound terms each time a term is broken out to subtract 1 and rewrite the number in CNF is always a smaller magnitude than that of the reduction by a constant factor at the same step, since the constant value used in the constant factor reduction is the highest n+1 value that the particular Goodstein sequence ever reaches. This would mean, in turn, that the Goodstein sequence reaches 0, since it corresponds one-to-one with the ordinal sequence. But at this point the fact that the ordinal sequence is strictly decreasing is no longer needed to prove that the Goodstein sequence terminates, because we have already proven this in the independent argument that was a necessary prerequisite for determining whether the ordinal sequence itself could actually be strictly decreasing. Without this independent knowledge, we cannot say that the ordinal sequence is strictly decreasing, and thus we cannot use the fact of the strictly decreasing nature of the ordinal sequence to conclude that the corresponding Goodstein sequence terminates.
Let us illustrate this with an example. Below are the first few elements in Goodstein sequence 11, each with its corresponding ordinal sequence element. We use O instead of γ for the ordinal sequence, but the process is the same:
G(11, 1) = 22+1 + 2 + 1; O(11, 1) = ωω+1 + ω + 1
G(11, 2) = 33+1 + 3; O(11, 2) = ωω+1 + ω
G(11, 3) = 44+1 + 3; O(11, 3) = ωω+1 + 3
G(11, 4) = 55+1 + 2; O(11, 4) = ωω+1 + 2
G(11, 5) = 66+1 + 1; O(11, 5) = ωω+1 + 1
G(11, 6) = 77+1; O(11, 6) = ωω+1
G(11, 7) = 88+1 - 1 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 7; O(11, 7) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 7
We may then choose a natural number to be the fixed number that ω is supposed to represent. For convenience, let ω = 2. Then, we have the following:
O(11, 1) = ωω+1 + ω + 1 = 22+1 + 2 + 1 = 11
O(11, 2) = ωω+1 + ω = 22+1 + 2 = 10
O(11, 3) = ωω+1 + 3 = 22+1 + 3 = 11
O(11, 4) = ωω+1 + 2 = 22+1 + 2 = 10
O(11, 5) = ωω+1 + 1 = 22+1 + 1 = 9
O(11, 6) = ωω+1 = 22+1 = 8
O(11, 7) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 7 = 7⋅22 + 7⋅27 + 7⋅26 + 7⋅25 + 7⋅24 + 7⋅23 + 7⋅22 + 7⋅2 + 7 = 1813
Right away, we can see that this sequence is not strictly decreasing. From step 2 to step 3, we see an increase of 1, step 4 is the same value as step 2, and step 7 sees a large increase from step 6, moving from 8 to 1813, and is larger in value than any of the previous steps. However, note that in the vicinity of the point where the constant chosen, in this case 2, begins to match n+1, where n is the step number – in this case, steps 1-3 – we can say that there was a strict decrease up to this point, then an increase, then a strict decrease until the sequence reached the point where the right-most single-exponent term reduced to 0. Then, at the next step, we saw a doubling of the previous right-most term from the last time the right-most reduced to 0 – in this case step 3, where the term was 4 before being reduced by 1 to 3. In step 7, the right-most term is now 8, and after it is reduced by 1 it becomes 7, which is what we see in the above expression. At this point, because we used 2 as our ω value, replacing ω with 2 in step 6 produces a much smaller number than replacing ω with 2 in step 7, since the sum of the terms in step 7 with a value of 2 for ω is considerably greater than the value of step 6 with 2 for ω. However, if we increase our ω constant from 2 to 7, the evaluations start to show signs of a change; in particular, the values of the expressions at steps 6 and 7 are closer to each other, proportionally speaking, than when ω was 2:
O(11, 6) = ωω+1 = 77+1 = 5,764,801
O(11, 7) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 7 = 7⋅77 + 7⋅77 + 7⋅76 + 7⋅75 + 7⋅74 + 7⋅73 + 7⋅72 + 7⋅7 + 7 = 12,490,401
But then what happens if we set ω = 8? As we can see below, the value is reduced from step 6 to step 7, by exactly 1 – and this is to be expected, since the standard Goodstein algorithm at step 7 would replace the 7s in the expression at step 6 with 8s and then subtract one, i.e., would replace 77+1 with 88+1 - 1. But if our constant is already 8, then the net result in the ordinal sequence expressions between steps 6 and 7 is that we are just subtracting 1. Below we also reproduce the entire sequence from steps 1 to 7, and the reader can see also that step 3 shows a net reduction from step 2 as well, rather than a net increase:
O(11, 1) = ωω+1 + ω + 1 = 88+1 + 8 + 1 = 134,217,737
O(11, 2) = ωω+1 + ω = 88+1 + 8 = 134,217,736
O(11, 3) = ωω+1 + 3 = 88+1 + 3 = 134,217,731
O(11, 4) = ωω+1 + 2 = 88+1 + 2 = 134,217,730
O(11, 5) = ωω+1 + 1 = 88+1 + 1 = 134,217,729
O(11, 6) = ωω+1 = 88+1 = 134,217,728
O(11, 7) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 7 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 7 = 134,217,727
So then does this mean that ω = 8 is the magic number for this ordinal sequence that will ensure that it will be strictly decreasing? It does not. Let us continue with ω = 8 and evaluate the values at some higher steps. The steps continue as follows:
O(11, 8) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 6 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 6 = 134,217,726
O(11, 9) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 5 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 5 = 134,217,725
O(11, 10) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 4 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 4 = 134,217,724
O(11, 11) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 3 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 3 = 134,217,723
O(11, 12) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 2 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 2 = 134,217,722
O(11, 13) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω + 1 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 + 1 = 134,217,721
O(11, 14) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 7⋅ω = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 7⋅8 = 134,217,720
We can see that the process of strict decrease continues. But at the next step, step 15, we must break out the right-most term in order to subtract 1 and keep the expression in CNF. To do this, we reduce the right-most term by a constant factor of 8, but we add to the end of the expression a value that is double the value we added at the end of step 7, the last time the right-most term reduced to 0; i.e., instead of adding 8 and then subtracting 1 to get 7, we add 16 and subtract 1 to get 15. Let us evaluate this:
O(11, 15) = 7⋅ωω + 7⋅ω7 + 7⋅ω6 + 7⋅ω5 + 7⋅ω4 + 7⋅ω3 + 7⋅ω2 + 6⋅ω + 15 = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 6⋅8 + 15 = 134,217,727
Note that this is an increase in numerical value from step 14 to step 15. In fact, this increase becomes more pronounced the more we continue this evaluation process. For steps 16-30, the ordinal sequence strictly decreases by 1 at each step, until again the right-most term has reached 0. At this point we have
O(11, 30) = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 6⋅8 = 134,217,712
Starting at step 23, the value becomes 134,217,719, which is 1 less than the value at step 14 that we increased from at step 15, and then it continues to reduce to 134,217,712 at step 30. But the values from steps 15-22 were all greater than (or equal to, in the case of step 22) the value at step 14, as well as values at numerous previous steps. But then what happens at step 31? In order to write step 31 in CNF, we must again break out the right-most term, and to do this we reduce the expression’s value again by a constant factor of 8, but we increase the expression’s value by twice the amount we did the last time the right-most term reduced to 0, and then subtract 1. Therefore, at step 31, we have the following:
O(11, 31) = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 5⋅8 + 31 = 134,217,735
This value is not only an increase from the value at step 30, but it is greater than almost all the values in the entire sequence thus far. Let us make one more round trip. After 31 more steps, the right-most term again reduces to 0, so we have
O(11, 62) = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 5⋅8 = 134,217,704
We then must break out the right-most term in this expression, and to do this we reduce the value of the expression by a constant factor of 8 but then increase it by double the amount of the increase from the last time the right-most term was reduced to 0, and then subtract 1. This gives us the following:
O(11, 63) = 7⋅88 + 7⋅87 + 7⋅86 + 7⋅85 + 7⋅84 + 7⋅83 + 7⋅82 + 4⋅8 + 63 = 134,217,759
Not only is this an increase from step 62, rather than a decrease, but the number at step 63 is now larger than the number that started the entire sequence, which was 134,217,737. The reader can verify that this pattern will continue, reducing by a constant factor of 8 each time and then increasing by twice the value of the previous increase the last time the right-most term reduced to 0. When the term that is reducing by the constant factor itself reduces to 0, then we will need to start breaking down the term with a 2 exponent just to the left of it, and then the expression will start reducing at each round trip by a constant factor of 82 rather than 8, but at this point the amount being added as the new right-bound terms will be substantially greater than this, so the net result will still be an increase. The same will occur with all subsequent left-bound terms, as they are broken down. This is jumping the gun a little, but it is, in fact, true that all Goodstein sequences terminate, and they do so by cannibalizing the left-bound terms starting from the right and proceeding further and further left. When the process gets to the left-most term, the net reduction at each round trip will be a factor of 88, which has a value of 16,777,216. This seems like a lot, but at this point the value of the corresponding increase due to the new right-bound terms will be so immensely greater than this that this value of just under 17 million will seem like a tiny speck of a number. In other words, beyond where our chosen constant for ω equal n, the ordinal sequence displays a pattern of strict decrease by 1 at each step punctuated every so often by an increase across steps. The behavior will differ a little if the constant we choose is not equal to an n at which the right-most term has reduced to 0, but overall the behavior will still show this pattern.
Then what if we chose a higher value for our constant? What if, instead of 8, we chose 16? Or 64? Or 50,000,000? For these values, the transition from step 6 to step 7 would show a decrease, as above in the case of the constant 8, but the decrease would be larger than a decrease by 1, and it would be larger the larger the constant we choose. However, as stated above, without any independent information about whether the Goodstein sequence itself terminates, we have no way of knowing whether a given Goodstein sequence will persist for long enough so that for any constant we choose, no matter how high, the above pattern will repeat itself, whereby there is a strict decrease for a while, but then the reduction by a constant factor combined with an always-duplicating right-most term and growing coefficients of the other right-bound terms at each round trip ensures that at a certain point we start seeing punctuated increases, as well as values that are greater than earlier values even within the periods after the beginning of new round trips where there is a strict decrease before the next beginning of a round trip. The standard Goodstein argument relies on the conclusion that the ordinal sequence, using the ω symbol, strictly decreases across steps, but the only way a “decrease” operation can be meaningful is if the ω symbol represents a constant value. But we have seen that for any constant value we choose, there is a fluctuation between increases and decreases beyond a certain point, and the increase at each round trip is substantially greater than the increase at all previous round trips, with this pattern showing no signs of changing. The only way in which the “strictly decreasing” comment could be correct is if there is a highest finite value that, when used as the constant to replace ω, would always be large enough such that the constant factor decrease at each round trip would more than compensate for the corresponding increase at the same step. But the only way to determine if there is such a value is to have an independent argument which proves that a given Goodstein sequence, or any Goodstein sequence, has such a value. Only then can the standard Goodstein argument legitimately conclude that the ordinal sequence for any Goodstein sequence is, or more correctly, can be made to be, strictly decreasing. As things stand, the standard Goodstein argument relies solely on the assumption that in using ω, which represent infinity in standard set theory, the “numerical value” of any step in the ordinal sequence is strictly smaller than the “numerical value” of all previous steps in the ordinal sequence, and, therefore, no matter how high the “constant” value would need to be to replace ω so that the sequence is strictly decreasing, the use of the ω symbol means that the standard Goodstein argument “has all possibilities covered.” But this is vague at best. Furthermore, this argument conflates the finite with the infinite, and is thus founded on a logical error, because it treats ω as a finitized infinity, i.e., as infinity but at the same time as a fixed quantity that can be manipulated arithmetically, and, in particular, that can be reduced from. The standard Goodstein argument has no information about the nature and behavior of the Goodstein sequences other than the assumption that they must terminate “given” that the ordinal sequences terminate. But without any other information about the nature of the Goodstein sequences, i.e., about their pattern of behavior, the most we can say is that if a Goodstein sequence terminates, then there will be a highest constant such that the ordinal sequence using that constant or any constant higher still will be strictly decreasing, but that if a Goodstein sequence does not terminate, then there is no such highest constant, and the behavior will be such that the gap between the beginning of the sequence through the initial strict decreasing to the point where the sequence begins its punctuated increases will become ever wider as the constant we choose becomes ever higher, but the point of punctuated increase will still inevitably be reached. The use of the ω symbol in the standard Goodstein argument can be seen as an attempt to preempt this inevitability, by saying that the “constant” chosen is actually higher than any constant that could be chosen that would inevitably lead to the beginning of the punctuated increases in the sequence, so that such an increase never starts, and therefore the argument is “correct” in saying that the ordinal sequence is strictly decreasing. However, this is not a valid argument, because ω cannot ever represent a constant, since it is infinity and so in order to avoid a logical contradiction it must be ever changing in value. Furthermore, if, for the sake of argument, we say that the ordinal sequence “counted down from infinity” in order to avoid the, for all we know, inevitable increases that would begin at a certain point in any Goodstein sequence which used a fixed value for ω, then the ordinal sequence would never terminate even though it would be strictly decreasing, because it would be starting from infinitely far away from the termination point. The standard Goodstein argument tries to have the best of both worlds, but ends up having nothing of either. It tries to ensure that the ordinal sequence is strictly decreasing by starting the sequence from an infinity point; but then it can never reach 0, because it starts infinitely far away from 0. On the other hand, it uses a constant symbol, ω, in easy-to-understand polynomial expressions, and thus makes it seem, based on our familiarity with standard polynomial expressions in algebra, that we are starting the ordinal sequence with a fixed numerical value, and thus a finite value, which we can then imagine without logical contradiction can, in fact, reach 0 after a finite number of reductions; but this is contradicted by the fact that the ω symbol is being used rather than a letter like x or y to represent a constant unknown, since ω represents the infinity of the natural numbers, which is not constant. But because we are now so familiar with treating ω as a constant in set theory, in our proofs and theorems, in ordinal arithmetic, etc., we do not skip a beat when it comes to using it to represent a constant in certain essential ways in the standard Goodstein argument. But, as we have seen, if we use ω as a constant, then without any independent information about whether a Goodstein sequence terminates, we cannot know for sure that the ordinal sequence could ever be strictly decreasing, and thus we cannot use such a conclusion to then conclude that the corresponding Goodstein sequence terminates. And, if we use ω to mean infinity to try to ensure that all our bases are covered, then we run afoul of the logical error of finitized infinity, and thus our argument does not make logical sense; the most we can say is that for any given Goodstein sequence if we find that the constant we chose leads to a punctuated increase scenario, we can decide to choose an even higher constant and then run through the process again to see whether we get to 0 before a punctuated increase scenario is again reached – and, again, we do not have enough information to say that this process could ever end, i.e., we do not have enough information to say whether, for any given Goodstein sequence, we will ever reach a constant that allows the ordinal sequence to be strictly decreasing. We cannot say that “infinity,” being the “highest” of all the natural numbers, has all possibilities covered, since no matter how high an actual constant we choose which still leads to the punctuated increase scenario, the “infinity” constant that we assumed in the argument is higher still, and so, effectively, is “infinitely far away” from encountering the strictly increasing scenario. This is not mathematical precision, but mathematical obfuscation. If we rid our thoughts and our arguments of the logical error of finitized infinity, this vagueness clears, and we can start to make intuitive sense of things again. Because of these considerations, then, we may conclude that the standard Goodstein argument does not prove that all Goodstein sequences terminate, or even that any of them does – the trivial ones that start with 1, 2, and 3 are not proven to terminate by use of the “strict decreasing” argument, but by a simple recognition of the pattern in the Goodstein sequence itself for each of these numbers, which we may then conceptually overlay onto the corresponding ordinal sequences, and when we do so it becomes obvious that there is a highest number that can be made the constant that will ensure the ordinal sequence is strictly decreasing. But notice that the conceptual path is still one whereby we obtained independent confirmation that the Goodstein sequence does terminate before we were able to clearly see that the ordinal sequence strictly decreases; it is just that since the pattern of termination in the Goodstein sequence is so obvious in these cases, it is harder to separate this out into a separate conception from the pattern we perceive in the ordinal sequence when we implicitly treat ω as constant, and this obviousness, in fact, makes it easier to treat ω as a constant, and to do so implicitly. Without a recognition of this pattern in the Goodstein sequence, whether this recognition comes from thinking about the Goodstein sequence itself or from pondering the ordinal sequence as an obvious representation of the Goodstein sequence, the standard Goodstein argument, which says, without any assistance beyond the supposedly perceived pattern in the ordinal sequence considered by itself, that the ordinal sequence is strictly decreasing, does not have enough information to conclude that the ordinal sequence is strictly decreasing, and so cannot be used to prove that the corresponding Goodstein sequence terminates. This is, again, on top of the fact that ω is used in the ordinal sequence, and thus the logical error of finitized infinity is assumed to be valid in the standard Goodstein argument, which by itself invalidates the standard Goodstein argument.
Let us discuss things in a bit more detail. The symbol ω in set theory is supposed to represent the infinity of the natural numbers, so how exactly are we supposed to “start” a sequence of fixed quantities, i.e., of numbers, that can then decrease and reach 0 after a finite number of steps, with ω, or any “arithmetic expression” involving it, somehow being the first fixed quantity in this sequence? And only after we start a sequence can we proceed to add additional elements to it by some iterative process or algorithm. In fact, as we have discussed, it is a contradiction to say that an infinity can be equal to a finite quantity, but this is one of the things which the Goodstein argument purports to do in the ordinal sequences. This is the same rock upon which the diagonal argument founders. The Goodstein argument treats ω as both finite and infinite at the same time – it treats it as if it is, somehow, a “fixed” quantity that is a “maximum” of the natural numbers, from which so long as we continue to reduce by a finite number at successive steps we will eventually reach 0; at the same time it treats ω as an infinite quantity by treating it as the highest of an infinite set, i.e., as higher than any number one may care to name, no matter how large. But if something is infinite, then it makes no sense to say that one may reduce it to 0 after a finite number of steps. And if a magnitude or number is finite, then it will never change or increase and there will always be magnitudes or numbers larger than it, so it cannot ever be infinite. Also, it makes no sense to say that we may reduce from infinity by one or more “infinite amounts,” in order to reduce to 0 from infinity in a finite number of steps, because this also conflates the finite with the infinite in saying that we are reducing from one number to another number, which is only logically meaningful if the amount being reduced by is finite, by an infinite amount – if we are being generous, we could say that at most reducing by an infinite amount means the end result will never be a fixed number, but instead will perpetually decrease; but the reality is that it makes no sense to reduce a number to another number unless all three numbers involved are finite.
The Wikipedia article on Goodstein’s theorem states that “if [the Goodstein ordinal sequence] terminates, so does [the original Goodstein sequence]. By infinite regress, [the original Goodstein sequence] must reach 0, which guarantees termination.”84 But how, exactly, can an “infinite regress” ever terminate? Comments such as this show the confusion involved in arguments that conflate the finite with the infinite. We (a) teach ourselves to become comfortable with the idea that there is, in some sense, a “highest” of the natural numbers, and we call this quantity ω, even though at the same time we acknowledge that there is no such highest number; (b) know that, clearly, 0 is a fixed magnitude; and so (c) draw the paradoxical conclusion that “somewhere out there” on the “real line” is the fixed ω point, or some fixed point that represents the “quantity” created out of some arithmetic expression involving ω, and that, therefore, since there is this fixed point “out there” which in some way represents our “highest” point under consideration, on the one hand, and the 0 point right here on the other, the “distance” between these points must be, however large, finite, and therefore we must be able to count down in finite increments from our higher number and eventually reach 0. Yet at the same time we, paradoxically, state that ω represents an infinite quantity, from which follow the facts that (a) it is not an actual quantity at all, because it never stops changing, and so neither it nor an arithmetic expression using it can ever serve as the starting point for a sequence of fixed numbers, and (b) since ω represents the first unit “number” which is greater in magnitude than any given natural number, it would be impossible, even if we were to imagine, for the sake of argument, that it could be a “fixed” quantity in some vague sense, to actually count down to 0 in a finite number of steps from this number or an arithmetic expression involving it, since if we could do this it would prove that this infinite quantity is finite, a contradiction. And it must be a finite number of steps, the “infinite regress” comment above notwithstanding, because the whole point of the Goodstein theorem is that since the Goodstein ordinal sequence is strictly decreasing and thus “always” reaches 0, and since each step in the original Goodstein sequence is mapped one-to-one with the steps in the Goodstein ordinal sequence, we may feel justified in concluding that the original Goodstein sequence reaches 0 after a finite number of steps, regardless of how many steps it takes – if even one Goodstein sequence could be shown to never reach 0 after a finite number of steps, however great, this would contradict the Goodstein theorem. But since the Goodstein sequences start with arithmetic expressions involving ω, then if we are to take ω to mean infinity we will never be able to reach 0 no matter how many iterations of the Goodstein algorithm are performed, and regardless of how large a finite number we reduce the “magnitude” of the expression by at each step; and, since the numbers in the Goodstein sequence are mapped one-to-one with the numbers in the ordinal sequence, this “shows” that no Goodstein sequence ever finishes!85 But we know that this is not true, because we know that Goodstein sequences that start with 2 and 3 finish in a short number of steps. This is an example of the kind of contradictory and confusing result obtained when an argument or proof is based on a logical error.
One may think to circumvent the problem whereby we need an infinite regress to be able to reduce to 0 in a finite number of steps by saying that, as with the above examples from Potter, at certain steps in the process the infinity of ω is reduced to a finite number by the algorithm, instead of just being reduced by 1 or by a particular, however large, finite quantity, and this can serve to reduce the ordinal sequence “faster,” possibly compensating for the fact that no matter how many 1s or finite quantities of any magnitude one subtracts from infinity, one will always still be left with infinity. But, again, this assumes that the ω expression in which one replaces an ω with a finite number, e.g., 3, is capable of being reduced in any meaningful way. For something to be reduced so that the result is a lesser amount after the reduction, it has to be a finite, fixed quantity to begin with, which ω is not, or at least is not supposed to be, and the quantity which the fixed quantity is reduced by must also be a fixed, i.e., finite, quantity. Something that is always changing inherently, such as an infinite “quantity” or a non-terminating decimal sequence, is not a number in the first place, because a number is a fixed magnitude. How many slices of pie, assuming 8 slices per pie, will be left from a continually increasing number of pies if you subtract 9 slices? The question is nonsensical, because it assumes both that you have a fixed quantity of pies from which you are subtracting 9 slices, and, at the same time, that the quantity of pies from which you are subtracting 9 slices is not fixed. But the Goodstein result depends crucially on the idea that the ordinal sequence is strictly decreasing, meaning the concept of numerical decrease of the ordinal sequence at each step is an essential part of the argument. The only way replacing ω with a finite number, such as 3, in an iteration of the Goodstein algorithm could “compensate” in the appropriate way to ensure the ordinal sequence and Goodstein sequence reach 0 at the same time is if the ordinal sequence is treated as nothing but a disguised copy of the Goodstein sequence, and then this compensation only works because the drops from ω to a finite number in the ordinal sequence always exactly match the points in the Goodstein sequence where an exponent or a base no longer participates in the process of increase by 1 at each step (see below), and because all Goodstein sequences do eventually terminate (again, see below); and in this case ω is not being treated as infinity, but only as a placeholder for n+1 at step n.
Also, the “faster” argument still assumes that there is a relation of some kind between the number of “numbers” and their rate of change as they (presumably) approach 0 in the ordinal sequence, on the one hand, and the number of numbers in the associated Goodstein sequence and their rate of change as they (presumably) approach 0, on the other. But this supposed correspondence is entirely presumptive. The ordinal sequence is supposed to be a string of strictly decreasing fixed quantities, but by making it so we have stripped the ordinal sequence of its mathematical relationship to the original Goodstein sequence, so that there is no longer any necessary relation between the way the Goodstein algorithm reduces an ω to, for example, a 3, or a 9, or a 47, or whatever, at certain steps in the production of the ordinal sequence and the number of steps it takes for this sequence to (presumably) reach 0, on the one hand, and the way the finite numbers in the Goodstein sequence itself change and the number of steps it takes for this sequence to (presumably) reach 0, on the other hand; i.e., we have removed the very thing which ensures that there is patterned connection between the two sequences, the one thing which alone could conceivably allow us to conclude that both sequences reach 0 at the same time. No such connection, or reason for such a connection, is provided by the Goodstein argument when it tells us that the ordinal sequence is strictly decreasing – we are just told that because the ordinal sequence is “strictly decreasing,” it must eventually reach 0, and, therefore, the Goodstein sequence must terminate at the same time. But there is nothing in this that says that the Goodstein sequence must terminate precisely when the ordinal sequence terminates. How are we to know that a given Goodstein sequence does not continue for another 9456789333 steps after this before terminating? Or that it takes far fewer steps for the Goodstein sequence to terminate than the ordinal sequence? Or that there even is a constant value for ω that allows the Goodstein sequence to reach 0 (if it does) at the same time as the strictly decreasing ordinal sequence? Or that even though an ordinal sequence has reached 0, the Goodstein sequence must terminate at all? After all, a Goodstein sequence maps one-to-one with at least a subset of the natural numbers, and since the natural number are infinite, and thus never end, it is at least possible under these assumptions for such a sequence to continue to any point whatsoever before it reaches 0, if it ever does. As stated above, without an independent argument that allows us to conclude that there is a highest n+1 that the Goodstein sequence reaches, which would simultaneously prove that the Goodstein sequence terminates, we do not have enough information to know whether the corresponding ordinal sequence does not always eventually revert to a pattern of punctuated increase; thus, if we rule out the logically contradictory option of starting at “infinity,” then the standard Goodstein argument does not provide any justification whatsoever for concluding that the ordinal sequence strictly decreases, and the assumption that it does, as stated above, completely strips it of any mathematical connection to its cor-responding Goodstein sequence, and thus of its ability to say anything at all about the Goodstein sequence’s behavior. But, again, this confusion is the result of a conflation of the finite with the infinite. We assume that we can start at an infinite quantity and, after a finite number of iterations of the ordinal sequence (but also, at the same time, an infinite number of iterations), we will be able to reach 0; and in one-to-one correspondence the Goodstein sequence eventually reaches 0 (presumably) at the same finite point, i.e., a point beyond which there is still an infinite number of natural numbers. But since the elements in the two sequences are supposed to correspond one-to-one, and since the Goodstein sequence terminates after a finite number of steps, the ordinal sequence must also terminate after a finite number of steps, and so for this reason it is, again, unjustified and misleading to use the ω symbol, given its standard meaning in set theory, in any way to indicate quantities or parts of quantities in the ordinal sequence. The only possible way that the ordinal sequence could be strictly decreasing and end at 0 after a finite number of steps is if it started at a finite number. If we choose to use the ω symbol as part of the arithmetic expressions in the elements of this sequence, then if this usage is to make logical sense the ω symbol can no longer mean infinity, i.e., it must be stripped of the very thing which it has been used this whole time to represent, and which is its only defining characteristic.
As stated, under the standard Goodstein argument we have no way of knowing how high the fixed value of ω must be in the ordinal sequence so that this sequence reaches 0 precisely when the Goodstein sequence does, or if there even is such a value. But this is implicitly acknowledged in the Goodstein argument itself by its use of ω, the symbol for infinity, to replace n+1 in the CNF of each Goodstein number, rather than, say, x to represent a constant unknown; in fact, the use of ω in the ordinal sequence can be seen as helping to gloss over the fact that in saying that the ordinal sequence is “strictly decreasing” the argument completely strips the ordinal sequence of any necessary mathematical relation to the corresponding Goodstein sequence, i.e., as helping to compensate for this loss of mathematical clarity by bringing in a concept that is inherently mathematically unclear itself but that, after over a century of collective will power, is believed by the majority of set theorists, so long as they do not think too clearly about it, to be a logically valid concept – the net result of which is the feeling that we have somehow gained in our understanding, when this is not the case. Saying that an infinite decreasing sequence of ordinals cannot exist because “the standard order < on ordinals is well-founded”86 does not help clear things up, because this assumes (a) that transfinite ordinals are numbers, i.e., fixed quantities, that can be placed in a strict decreasing sequence in the first place, and (b) that it is possible to get down to 0 after a finite number of steps from an infinite quantity. Both of these assumptions are logically flawed.
Also, this is not helped by remembering that there is a one-to-one relationship between elements of the Goodstein sequence and elements of the ordinal sequence, because depending on the value we choose for ω, there may indeed be a one-to-one relationship like this until the ordinal sequence reaches 0, but, again, there is no guarantee that the Goodstein sequence will also have reached 0 at this point, or that it will not have reached 0 sooner than the ordinal sequence. If there is any independence at all between the two sequences – and such independence is necessary if we are to conclude that the ordinal sequence is strictly decreasing in general, which is what the Goodstein argument states – then there is no inherent or necessary relationship between a particular element of a Goodstein sequence and its cor-responding element in the ordinal sequence which is made up simply, and arbitrarily, by replacing n+1 in the CNF of the Goodstein number at the given step with ω; i.e., there is no inherent or necessary reason why n+1 should be replaced by the same value, ω, at every step to produce the resulting “number” at that step of the ordinal sequence, and there is no inherent or necessary reason why doing so would produce a sequence of elements that must correspond bijectively with the sequence of elements of the original Goodstein sequence. This lack of sufficient precision, again, is acknowledged implicitly in the Goodstein argument by making the replacement symbol ω, and by not specifying a particular reason why the relationship between corresponding elements in the two sequences makes sense or is justified in such a way as to guarantee that if the Goodstein sequence reaches 0 then the ordinal sequence reaches 0 at the same point or vice versa. In fact, the acceptance of the supposed validity of the Goodstein argument depends crucially on our already having accepted as valid and precise this lack of precision in other, related areas of set theory. Once things are clarified, it is the Goodstein argument itself that can be seen to lack precision.
But what if, after we chose to treat ω as a fixed quantity in the first element of the ordinal sequence, we then specified that the value of ω is to be reduced by 1 at each step in the sequence, to correspond with the increase by 1 of n+1 at each step in the Goodstein sequence? But this does not solve the correspondence problem; at best, it further disguises it. It is true that ω would be changing as the sequence progressed, but each instance of it would still be fixed, and so each element in the sequence could still legitimately be called a number. It is also true that such a sequence would eventually reach 0, assuming we started with ω equal to a finite number, since eventually ω would reduce to 0 and then all that would be left would be a constant, the right-most term, which would inevitably reduce to zero in one-step increments of 1; though this sequence would not be strictly decreasing. But there is still nothing in this modified procedure that would give us reason to believe that this altered ordinal sequence would be guaranteed to reach 0 at the same time the Goodstein sequence did (if it did). If a particular Goodstein sequence never reaches 0, then no matter how high we make ω, the ordinal sequence will always reach 0 when the Goodstein sequence has still not reached 0. The standard proof of the Goodstein theorem obscures this by using the ω symbol as the replacement symbol in the ordinal sequence, since ω represents, in a vague sort of indeterminate way, any high or large number, no matter how high or how large. As such, it has all the possibilities “covered,” so that regardless of which number the ordinal sequence needs to start with in order to “match” a given Goodstein sequence, the starting point will always be “high enough” to ensure that for any Goodstein sequence the corresponding ordinal sequence can be thought to “always” reach 0 at the precise point the corresponding Goodstein sequence reaches 0 – and, even if the Goodstein sequence never reaches 0, technically this possibility is covered as well because the starting point of the ordinal sequence makes use of the ω symbol, the infinite quantity, and if an infinite quantity can reach 0 by a finite number of steps, then so can a Goodstein sequence that never reaches 0 also reach 0, since it is able to take, if necessary, an infinite number of steps, in which each step corresponds to an element of the infinite ordinal sequence, to ensure that it gets to this point. As stated above, this is not mathematical precision, but mathematical obfuscation, and it has seemed to be mathematical precision for as long as it has because set theory has become ingrained with the belief that it is possible to finitize the infinite and arithmetically manipulate these finitized quantities, i.e., that such manipulations are meaningful. As the chorus goes, “Addition, multiplication and exponentiation of [transfinite] ordinal numbers are well defined.”87 But these operations are only “well defined” because we have treated these finitized infinities for a long time now as if they were actual finite quantities that can be meaningfully manipulated arithmetically, and so over the years and decades we have built up agreed-upon procedures for such manipulations. In fact, this agreement itself among practitioners adds yet another reinforcement to the finitization process, and thus further reinforces our sense of justification in treating infinite quantities as if they were finite; this, in turn, makes it that much harder for us to recognize the logical errors in arguments that are based on the conflation of the finite and the infinite, such as the standard Goodstein argument.
But if, as we have seen, there are logical errors in the conception of ω when used in the ordinal sequence as an infinite quantity; and there are also fatal flaws in the argument when ω is thought of as a finite quantity; and since these are the only two possible options; then we have shown that the Goodstein proof is flawed, and thus does not, in fact, prove that all Goodstein sequences terminate. But it is true that all Goodstein sequences terminate. So if the standard Goodstein argument is inadequate, how might it be modified in order to produce the correct result by means that are clear and logically valid?
Let us look at an example of a Goodstein sequence on a more extended scale to try to get a more concrete understanding of the phenomenon. We will look this time at the Goodstein sequence for the number 5. Below is a list of some of the elements in this sequence.
G(5, 1) = 5 = 22 + 1
G(5, 2) = 33 + 1 – 1 = 33
G(5, 3) = 44 – 1 = 3⋅43 + 3⋅42 + 3⋅4 + 3
G(5, 4) = 3⋅53 + 3⋅52 + 3⋅5 + 3 – 1 = 3⋅53 + 3⋅52 + 3⋅5 + 2
G(5, 5) =3⋅63 + 3⋅62 + 3⋅6 + 2 – 1 = 3⋅63 + 3⋅62 + 3⋅6 + 1
G(5, 6) = 3⋅73 + 3⋅72 + 3⋅7 + 1 – 1 = 3⋅73 + 3⋅72 + 3⋅7
G(5, 7) = 3⋅83 + 3⋅82 + 3⋅8 – 1 = 3⋅83 + 3⋅82 + 2⋅8 + 7
G(5, 8) = 3⋅93 + 3⋅92 + 2⋅9 + 7 – 1 = 3⋅93 + 3⋅92 + 2⋅9 + 6
G(5, 9) = 3⋅103 + 3⋅102 + 2⋅10 + 6 – 1 = 3⋅103 + 3⋅102 + 2⋅10 + 5
G(5, 10) = 3⋅113 + 3⋅112 + 2⋅11 + 5 – 1 = 3⋅113 + 3⋅112 + 2⋅11 + 4
G(5, 11) = 3⋅123 + 3⋅122 + 2⋅12 + 4 – 1 = 3⋅123 + 3⋅122 + 2⋅12 + 3
G(5, 12) = 3⋅133 + 3⋅132 + 2⋅13 + 3 – 1 = 3⋅133 + 3⋅132 + 2⋅13 + 2
G(5, 13) = 3⋅143 + 3⋅142 + 2⋅14 + 2 – 1 = 3⋅143 + 3⋅142 + 2⋅14 + 1
G(5, 14) = 3⋅153 + 3⋅152 + 2⋅15 + 1 – 1 = 3⋅153 + 3⋅152 + 2⋅15
G(5, 15) = 3⋅163 + 3⋅162 + 2⋅16 – 1 = 3⋅163 + 3⋅162 + 16 + 15
G(5, 16) = 3⋅173 + 3⋅172 + 17 + 15 – 1 = 3⋅173 + 3⋅172 + 17 + 14
G(5, 17) = 3⋅183 + 3⋅182 + 18 + 14 – 1 = 3⋅183 + 3⋅182 + 18 + 13
G(5, 18) = 3⋅193 + 3⋅192 + 19 + 13 – 1 = 3⋅193 + 3⋅192 + 19 + 12
G(5, 19) = 3⋅203 + 3⋅202 + 20 + 12 – 1 = 3⋅203 + 3⋅202 + 20 + 11
G(5, 20) = 3⋅213 + 3⋅212 + 21 + 11 – 1 = 3⋅213 + 3⋅212 + 21 + 10
G(5, 21) = 3⋅223 + 3⋅222 + 22 + 10 – 1 = 3⋅223 + 3⋅222 + 22 + 9
G(5, 22) = 3⋅233 + 3⋅232 + 23 + 9 – 1 = 3⋅233 + 3⋅232 + 23 + 8
G(5, 23) = 3⋅243 + 3⋅242 + 24 + 8 – 1 = 3⋅243 + 3⋅242 + 24 + 7
G(5, 24) = 3⋅253 + 3⋅252 + 25 + 7 – 1 = 3⋅253 + 3⋅252 + 25 + 6
G(5, 25) = 3⋅263 + 3⋅262 + 26 + 6 – 1 = 3⋅263 + 3⋅262 + 26 + 5
G(5, 26) = 3⋅273 + 3⋅272 + 27 + 5 – 1 = 3⋅273 + 3⋅272 + 27 + 4
G(5, 27) = 3⋅283 + 3⋅282 + 28 + 4 – 1 = 3⋅283 + 3⋅282 + 28 + 3
G(5, 28) = 3⋅293 + 3⋅292 + 29 + 3 – 1 = 3⋅293 + 3⋅292 + 29 + 2
G(5, 29) = 3⋅303 + 3⋅302 + 30 + 2 – 1 = 3⋅303 + 3⋅302 + 30 + 1
G(5, 30) = 3⋅313 + 3⋅312 + 31 + 1 – 1 = 3⋅313 + 3⋅312 + 31
G(5, 31) = 3⋅323 + 3⋅322 + 32 – 1 = 3⋅323 + 3⋅322 + 31
G(5, 32) = 3⋅333 + 3⋅332 + 31 – 1 = 3⋅333 + 3⋅332 + 30
G(5, 33) = 3⋅343 + 3⋅342 + 30 – 1 = 3⋅343 + 3⋅342 + 29
G(5, 34) = 3⋅353 + 3⋅352 + 29 – 1 = 3⋅353 + 3⋅352 + 28
G(5, 35) = 3⋅363 + 3⋅362 + 28 – 1 = 3⋅363 + 3⋅362 + 27
⋮
G(5, 61) = 3⋅623 + 3⋅622 + 2 – 1 = 3⋅623 + 3⋅622 + 1
G(5, 62) = 3⋅633 + 3⋅632 + 1 – 1 = 3⋅633 + 3⋅632
G(5, 63) = 3⋅643 + 3⋅642 – 1 = 3⋅643 + 2⋅642 + 63⋅64 + 63
G(5, 64) = 3⋅653 + 2⋅652 + 63⋅65 + 63 – 1 = 3⋅653 + 2⋅652 + 63⋅65 + 62
G(5, 65) = 3⋅663 + 2⋅662 + 63⋅66 + 62 – 1 = 3⋅663 + 2⋅662 + 63⋅66 + 61
⋮
G(5, 126) = 3⋅1273 + 2⋅1272 + 63⋅127 + 1 – 1 = 3⋅1273 + 2⋅1272 + 63⋅127
G(5, 127) = 3⋅1283 + 2⋅1282 + 63⋅128 – 1 = 3⋅1283 + 2⋅1282 + 62⋅128 + 127
G(5, 128) = 3⋅1293 + 2⋅1292 + 62⋅129 + 127 – 1 = 3⋅1293 + 2⋅1292 + 62⋅129 + 126
⋮
G(5, 255) = 3⋅2563 + 2⋅2562 + 62⋅256 – 1 = 3⋅2563 + 2⋅2562 + 61⋅256 + 255
⋮
G(5, 2097151) = 3⋅20971523 + 2⋅20971522 + 49⋅2097152 – 1 = 3⋅20971523 + 2⋅20971522 + 48⋅2097152 + 2097151
⋮
G(5, 8589934591) = 3⋅85899345923 + 2⋅85899345922 + 37⋅8589934592 – 1 = 3⋅85899345923 + 2⋅85899345922 + 36⋅8589934592 + 8589934591
⋮
G(5, 549755813887) = 3⋅5497558138883 + 2⋅5497558138882 + 31⋅549755813888 – 1 = 3⋅5497558138883 + 2⋅5497558138882 + 30⋅549755813888 + 549755813887
⋮
G(5, 2.25⋅1015) = 3⋅(2.25⋅1015)3 + 2⋅(2.25⋅1015)2 + 19⋅(2.25⋅1015) – 1 = 3⋅(2.25⋅1015)3 + 2⋅(2.25⋅1015)2 + 18⋅(2.25⋅1015) + (2.25⋅1015 - 1)
⋮
G(5, 2.95⋅1020) = 3⋅(2.95⋅1020)3 + 2⋅(2.95⋅1020)2 + 2⋅(2.95⋅1020) – 1 = 3⋅(2.95⋅1020)3 + 2⋅(2.95⋅1020)2 + (2.95⋅1020) + (2.95⋅1020 - 1)
⋮
G(5, 5.9⋅1020) = 3⋅(5.9⋅1020)3 + 2⋅(5.9⋅1020)2 + ((5.9⋅1020) - 1)
⋮
G(5, 1.18⋅1021) = 3⋅(1.18⋅1021)3 + 2⋅(1.18⋅1021)2 – 1 = 3⋅(1.18⋅1021)3 + (1.18⋅1021)2 + ((1.18⋅1021)2 -1)
In the above sequence, at the point where we began using scientific notation the numbers were rounded off to two decimal places. We can see that even to get rid of just the last two terms of G(5, 63), both of which have an exponent of 1, it takes over 1021 steps, and in the meantime the bases of the terms to the left of this have increased by a corresponding amount. Nonetheless, it can still be seen that while the bases of the left-bound terms do continue to increase, and continue to make the sum considerably greater with each step, the algorithm regularly pulls terms out of the left-hand part of the expression, starting from the far right but progressing further and further left; and after a while any given right-most term always eventually reaches 0, and then at the next step the new right-most term (which up to then was the second-right-most term) is broken down and 1 is subtracted. By the same reduction process applied now to the new right-bound terms, we can see that little by little the coefficients and exponents monotonically reduce in all the new right-bound terms whose exponents are less than n+1, until eventually even the bases of these terms stop participating in the process of increase by 1 at each step, and the left-most of these new right-bound terms eventually drops to 0. Since no additional terms are added on the left of the left-most term of the expression at any step, this strongly suggests that no matter how large the numbers in this Goodstein sequence become, they will eventually drop to 0, i.e., the Goodstein sequence will eventually terminate. This illustration also suggests that this will be the case for all Goodstein sequences, since the algorithm that generates the successive numbers for any Good-stein sequence is the same as that which generates the numbers for Goodstein sequence 5. What actually ends up happening in all Goodstein sequences is that this pattern progresses until the Goodstein number is the sum of two single-exponent bases both with coefficient 1, with the left term equal to n+1 and the right term equal to n, at which point there will be no further net change in the value of the Goodstein number for another n+1 steps, and then after this point there will be no number in the expression, not even the base of the left-most term, which at this point is the only term in the expression and which has coefficient 1 and exponent 1, that matches n+1 (the base of the left-most term at this point is equal to n), and, therefore, at each of the subsequent steps in the sequence, the value of the Goodstein number, which is, of course, finite, will reduce by 1, until the sequence finally terminates after another n steps. In fact, the foregoing is the outline for a valid proof of the Goodstein result. A proof, on the other hand, that is based on conflating the finite with the infinite is not a valid proof, because it is based on a logical error, even if in the course of using the argument we do end up drawing the correct conclusion.
As with the continuum hypothesis, there is no way to resolve the contradictions inherent in an argument based on a logical error on the basis of the contradictions themselves. We cannot continue to assume that the conflation of the finite and the infinite is logically justified, and at the same time find the way to clear up these errors and misconceptions. We must recognize the logical error for what it is, and only then can we start to find our way out of the mire of half-ideas, non-ideas, paradoxes, and seemingly miraculous results and conclusions. The standard proof of the Goodstein theorem is seemingly miraculous, in that it appears to prove something substantial with a relatively small amount of effort – like the diagonal argument. There is no reason why valid proofs with this kind of asymmetry cannot exist. If something seems too good to be true, this does not necessarily mean that it is not true. But, as the saying goes, extraordinary claims require extraordinary evidence. In the case at hand, and in other similar cases, we may say that extraordinary mathematical results require that we review our premises and assumptions with, as it were, a finer-toothed comb than we usually do, because chances are higher in such cases that one or more of our premises or assumptions are flawed. It may be the case that we still draw the correct conclusion, but if we look more closely in such cases we will realize that it is not the aforementioned premises or assumptions that allowed us to draw the correct conclusion, since these are, after all, flawed, but rather certain other related feelings and intuitions that, in spite of the flawed premises and assumptions, nonetheless kept us on the right track well enough to allow us to draw the correct conclusion anyway. We may then use the correct result fruitfully in other areas of research without knowing that the proof we believe produced the result could not, in fact, logically produce it; but the fruitfulness of application in other areas reinforces the belief that the proof itself is valid, as well as the premises and assumptions on which it is based. Often, only when we are forced to re-examine the premises due to other, at first seemingly unrelated, problems and investigations do we actually take the time to properly reexamine them, and if the other problems and investigations are significant enough, or foundational enough, we may then come to understand the flaw in the proof which we had up to that point considered valid.
Before we move on, let us revisit the topic of the idea implicit in the Goodstein argument that ω represents a fixed quantity, which is the only way in which the statement, “the ordinal sequence must be strictly decreasing,” under the conditions and assumptions of the standard Goodstein argument, can make sense, even partially. As we saw, there are flaws in this interpretation which prevent the argument from actually proving the Goodstein result. In light of this flaw, why does it nonetheless seem that the argument could still be true, that it still makes sense in a certain way? The reason for this was discussed earlier. Goodstein sequences do all eventually terminate, and this implicit understanding, or feeling, which comes from thinking about the nature and pattern of Goodstein sequences in the context of their actual numerical expressions, is conceptually overlain onto the argument that uses ω expressions and ordinal sequences, and onto the thought that sees a superficial decrease by 1 at each step for the first few steps in the ordinal sequence as possibly in some way translating into a strict decrease for the entire ordinal sequence; the similarities accentuated by this, combined with the fact that we have already assumed that there is no logical error in using ω in arithmetic expressions or in subtracting 1, or any finite quantity, from an expression that uses ω in one or more of its terms, and that there is no logical error in the idea that ω is the highest natural number with a fixed position in the sequence of numbers and can thus be treated in essential ways as if it were a finite number, allow us to mentally conflate and intermix these overlain concepts, so that we obtain the correct result, but in the context of a flawed proof. Specifically, even though we implicitly conceive of ω as a fixed, unchanging quantity whose arithmetic expressions we are constantly reducing at each step in the sequence, the reality is that before we involve ω in the expression at the next step in the sequence, we treat the Goodstein expression at the current step in terms of the actual numbers that make it up, first replacing ω at the current step with n+1, then bumping up to the next step and replacing n+1 with n+2, subtracting 1, and then rewriting, if necessary, the result in CNF. Only then do we replace n+2 (which, at the new step, is now n+1 again) with ω. In other words, the reason all ordinal sequences eventually terminate is precisely that all Goodstein sequences eventually terminate, and the only thing that the ω character at each step does is serve as a placeholder for n+1; in yet other words, when the Goodstein sequence terminates, the ordinal sequence terminates at the same time precisely because an ordinal sequence is nothing but a disguised copy of its corresponding Goodstein sequence. The fact that it is the ω symbol that replaces n+1 at each step instead of a different character such as a or b or x or y – or better yet, something nondescript like □ – throws us off track, making us think that somehow in order to prove the result infinity is or must be involved. But actually, the ω symbol, as used in the Goodstein argument, only ever maps one-to-one with the finite n+1 values, and thus the value that ω is a placeholder for is always finite and changes at every step, specifically it increases by 1 at every step. In fact, it is this mapping of ω to n+1 that is the only way to interpret the value of ω in the Goodstein argument that allows for an inherent or mathematically necessary connection between the Goodstein sequence and the ordinal sequence; but then ω no longer in any way represents infinity, and we also cannot say that the ordinal sequence is strictly decreasing, because since the ordinal sequences is nothing but a disguised copy of the Goodstein sequence, the ordinal sequence numbers increase precisely when the Goodstein sequence numbers increase, and decrease precisely when the Goodstein sequence numbers decrease. This also means that in spite of the use of the ω symbol in the ordinal sequence expressions, the only valid way to interpret the ordinal sequence expressions is also one in which there is no independence at all between the Goodstein sequence and the ordinal sequence; therefore, any conclusion that is based, even implicitly, on the idea that these two sequences were discovered even partially on the basis of independent mathematical means and that a “surprising connection” between the two shows that they both always terminate at the same time, is a conclusion based on an incorrect assumption, and therefore cannot be considered part of a valid proof of the Goodstein result.
However, as I have said, every Goodstein sequence does terminate. Let us, then, give a proof of this fact, one that does not rely in any way on the conflation of the finite with the infinite or on the “convenient confusion of concepts” that such conflation can sometimes engender. First, think back to the Goodstein sequence for the number 5 and the ordinal sequence for 51 above to use as reference points. Every Goodstein number in CNF is a sequence of terms, from left to right, that have + signs between them and whose exponents decrease as we move from terms on the left to terms on the right. But any term sufficiently far to the right, and every term thereafter, will have an exponent that is less than n+1 at step n. At each successive step, the exponents for these right-bound terms will not participate in the successive increase by 1 that happens to the exponents that are sufficiently far to the left in the expression, though the bases of most of these right-bound terms will continue to participate in this increase. However, if we restrict ourselves to the right-most term, then in all steps that do not involve the breaking down of a term in order to subtract 1, neither its base nor its exponent will participate in the increase by 1 process at successive steps, and its exponent will be 1. Therefore, since 1 is subtracted from the overall expression at each step, this right-bound term will eventually reduce to 0, since there is nothing in this term to compensate for the decrease by 1 at each step. Then, at the step beyond this point, every remaining term participates in the increase by 1, either in its base alone or both its base and exponent, and then 1 is again subtracted from the resulting value. But this expression is no longer in CNF, since it contains a minus sign. So, this expression must be rewritten in CNF before the next iteration of the process. But to do this, we must reduce the value of the right-most term (not counting the “–1” term at the very end) either (a) by reducing its coefficient by 1, or (b) if its coefficient is already 1, by reducing its exponent and adding a new coefficient. The remainder after this reduction in the right-most term (again, not counting the “–1” term at the very end) is then made into terms with smaller exponents to the right of the reduced term. Further, these new terms will be written to base n+1, and the “–1” term at the end will be eliminated by subtracting 1 from the right-most of these new terms, which will always be simply the base number (i.e., n+1) at that step with a “1” exponent and “1” coefficient, meaning that after subtracting 1 from this right-most term, we are left with a right-most term that will not increase at any subsequent step, but will only decrease. Further, in all of these new terms, the exponent will either be less than n+1 or will itself participate in the same reduction process that the entire expression participates in within the context of the exponent expression itself. Also, at subsequent steps all of these right-bound terms except the right-most one will see their bases increase as well. But since these terms’ exponents either do not increase anymore or participate in the overall reduction process themselves at a nested level, eventually even these terms will reduce to an exponent of 1 and a coefficient of 1, in sequence from the right-most of them to the left-most of them, during which process the base itself for each term in turn will begin to decrease until it reaches 0. Since the number of terms in the expression never increases to the left of the left-most term, then eventually all the terms to the right of the left-most term will reduce to 0 by the above process. Then, in the next step, the left-most term will see its exponent reduced by 1, because the left-most term will have to be broken out in order for the expression to remain in CNF after subtracting 1. At this point, the exponent of the left-most term will continue to participate in the increase by 1 process only as long as it takes to reduce its value to n at step n, and then the exponent of the left-most term no longer participates in the process of increase by 1 at each step. Such reduction of exponents to the point at which the exponent of a term no longer participates in the process of increase by 1 is guaranteed to happen for all terms, both for the left-most term and all right-bound terms, because the Goodstein sequence always begins with a finite natural number, and as such, its CNF to base 2 at step 1 is always finite in terms of the number of levels of nesting of the exponents in its terms. What this means is that within the exponent expression of a given term, eventually the final, highest level of nesting will be reached, and, by the inevitable and interminable process of reduction by 1 every so often at this highest nested level as the sequence progresses, this level’s exponents will all eventually be less than n+1, and will thus no longer participate in the increase by 1 process at subsequent steps; therefore, these terms will eventually reduce to 0, and this will then force the next lower level of the nested exponent expression of the given term to begin the same process, and thus to also reduce to the point that its exponents are all less than n+1 as well. This process will continue until the direct exponent of the base number of the term is reached and made less than n+1, and at this point the entire exponent is a single number less than n+1, and thereafter can no longer increase, meaning it will eventually reduce to 1.
We left off at the point where the exponent of the left-most term is now n at step n. Therefore, as the steps progress, only the base of the left-most term and the bases of the new right-bound terms with the same base participate in the process of increase. But, per the above pattern of reduction, all the right-bound terms will eventually decrease to 0, at the next step after which the coefficient of the left-most term will reduce by 1 and the remainder will be broken out into new right-bound terms, from which 1 will be subtracted. In this way, the coefficient of the left-most term will eventually reduce to 1, after which the process will repeat with the reduction of the exponent of the left-most term by 1 again, the coefficient of the left-most term now being equal to the new, larger value of the base minus 1, and the remainder again broken out into right-bound terms from which 1 is subtracted. Eventually, then, the exponent of the left-most term will reduce to 2 and its coefficient to 1, and all the right-bound terms up to that point will have reduced to 0, so that at the next step the exponent of the left-most term reduces to 1, its coefficient is made equal to the new, even larger value of the base minus 1, and the remainder is a single right-bound term equal to the value of the base, from which 1 is subtracted. But then eventually the coefficient of the left-most term will reduce to 2 and all right-bound terms again to 0, at which point the new, even larger base value of the left-most term will increase by 1, will have its coefficient reduced to 1 and will be followed by a single right-bound term that is equal to the new base value of the left-most term, from which 1 will be subtracted. Then, this new single right-bound term will reduce by 1 at each step, while at the same time the left-most term will increase by 1 at each step, so that the sum of these two single numbers will remain constant across another n steps. This leaves a single term with 1 as its coefficient and its exponent and whose base at step n is equal to n+1. At the next step, this number is increased by 1, but then reduced by 1, and so at this next step it is no longer n+1 at step n, but rather n at step n. Thereafter, this single base value itself no longer participates in the process of increase by 1 at each step, which means that nothing in the Goodstein expression participates any longer in the increase process. Therefore, after another n steps the Goodstein sequence terminates, i.e., reaches 0. This argument is valid no matter what number the Goodstein sequence begins with, because regardless of the starting number, or the number of terms needed to write the starting number in CNF to base 2, there will never be terms that are added to the left of the left-most term in this initial base-2 expression, and so since all right-bound terms and all exponent expressions, including the most deeply nested ones, inevitably reduce to 0, i.e., the reduction process never stops cannibalizing the next-left terms and next-lower exponent expressions of each term per the process spelled out above, eventually all terms, including the left-most term, will be fully cannibalized, and thus the entire expression will always reduce to 0.
The above proof is not presented by means of detailed mathematical formalism, but such formalism could be provided that would match the progression of statements in this prose-based proof. As we have seen, the numbers in Goodstein sequences of even small initial values increase quite rapidly. Such a rapid increase from such small initial values, and such massively huge numbers in general, can make it almost seem, in a vaguely murky sort of way, as if, beyond a certain starting number, the Goodstein numbers “brush up against” infinity, even if they may not actually “reach” infinity. This, in turn, can make it seem reasonable to bring in the concept of finitized infinity, via set theory’s use of the ω symbol, to try to help us understand the ultimate fate of Goodstein sequences, because Goodstein sequences and Goodstein numbers seem, in a sense, to “pass into the realm” or “pass within the reach” of infinity, and so it can seem that whatever we feel we know about infinity might be useful in helping us understand Goodstein sequences. The massively rapid increase of Goodstein sequences can also make us feel, when we try to investigate them, like we do not even have a chance to get a handle on their nature before they just completely spiral far beyond our control, and this, in turn, can make us feel a certain level of hopelessness in being able to fully grasp their nature and ultimate behavior. But we should remember that the natural numbers are infinite, and as such, no matter how large a particular number in a Goodstein sequence is, there will always be an infinite number of natural numbers larger still. Even if one or more Goodstein sequences did not terminate, which as we just saw is not the case, no matter how high the sequence got, the numbers produced by the sequence would still be well within the realm of countable infinity, which, as we have seen, is the only logically valid conception of infinity. Further, since the Goodstein sequences are produced by a pattern, then all it takes to prove whether the sequences terminate or not is an appropriately insightful understanding of the pattern, i.e., of the results it produces. In the realm of patterns, which can only occur and are only meaningful within the context of countable infinity, it is never necessary to bring into the mix a conflation of the finite with the infinite in order to prove a valid result, and, as the standard Goodstein argument illustrates, doing so produces at best only “convenient confusion” and false positives. Note also that this conclusion takes into account the usefulness of things like the limit concept in calculus, because the limit concept is not an attempt at proof that the finite can be made equal to the infinite, and does not depend in any essential way on these two things being equal; rather, it depends on a glossing over of this conflation where the conflation does not cause any problems in mathematical or scientific work, due to the desire for and the usefulness of approximations and the detection of patterns in infinite sequences in the practical contexts in which the limit idea is useful. Statements or proofs like the standard Goodstein argument, on the other hand, directly rely on the conflation of the finite with the infinite, and, as with CH itself, such reliance will always result in errors, flaws, contradictions, vagueness, and confusion.
We will now look at the “strictly decreasing” part of the Goodstein argument from yet another angle. We emphasize again that only because every Goodstein sequence eventually terminates is it possible for the corresponding ordinal sequence to terminate. The ordinal sequence is built up in lockstep with the original Goodstein sequence, so that at every step the next Goodstein number has to be created per the standard Goodstein algorithm before ω is then brought in to replace n+1 as the last part of the process at that step. But then what ω does in this process is to completely negate, or mask, the increase by 1 which happens at that step for the left-bound bases and exponents, instead making it appear, without the argument explicitly saying so, that these bases and exponents are the same value as they were in the previous step. Then, as the left-bound terms are slowly broken down into new right-bound terms, and as these terms gradually reduce to 0, and as levels of exponent nesting in terms which have such nesting also gradually reduce to 0, the standard Goodstein process takes more and more exponents and bases out of the running, by reducing them so they no longer participate in the increase by 1 process at each step. But in replacing the left-bound bases and exponents with ω, we continue to completely mask the increase by 1 that still continues to happen for the left-bound terms, both in their bases and their exponents. In other words, by replacing all numbers that we have increased by 1 at a given step with ω, and then implicitly thinking of ω as a fixed quantity, i.e., a quantity that does not change in value across steps, it can easily seem, at least initially, that the ordinal sequence is strictly decreasing, since it would seem that the net result of this process at each step is to decrease the value of the numerical expression by at least 1. In this process, we do not subtract 1 from an expression that actually includes infinity or an infinite “quantity”; rather, we subtract 1 from an expression in which we implicitly assume that the ω character is to be thought of as a fixed, i.e., a finite, quantity, in order for the concept “reduce” or “decrease” to be meaningful. But the ordinal sequence reaches 0 at the same time as the Goodstein sequence not because of any magic brought in by reference to infinity, but because the ordinal sequence is identical in all essentials to the Goodstein sequence at every step, so if the Goodstein sequence reaches 0, then of course the ordinal sequence will reach 0 at the same step. But remember that all Goodstein sequences reach 0 after a finite number of steps; and yet, we have used the ω symbol in their ordinal sequences to indicate that we have started “at infinity” in some vague sense for each ordinal sequence. How, then, does it make sense to say that we have started at infinity and yet reduced the ordinal sequence to 0 after a finite number of steps? Of course, this does not make sense. The only reason the proof seems to work is that in the use of ω in the proof we have completely negated ω’s defining characteristic of being infinite. But if we think of ω in the ordinal sequence expressions as simply being used to mask the increase by 1 at each step of the left-bound bases and exponents, then the ordinal sequence can be thought of as a way to make more obvious the fact that Goodstein sequences all eventually terminate by hiding unnecessary detail and accentuating the pattern of change in the sequence’s CNF expressions, and thus as a way to facilitate a valid proof; but it is misleading to use the ω symbol for this purpose, because ω already means “infinity” in set theory, while the only way to make the basic form of the standard Goodstein argument part of a valid proof is to think of ω as a placeholder. As such, it would be more appropriate to use a regular variable, such as x or y, or even better, as stated above, a more placeholder-esque symbol such as □, since the only use that this symbol has is as a mask to cover up the added complexity in the Goodstein expressions of increase by 1 of the left-bound bases and in the left-bound exponents, and as such it does not represent an actual number or fixed quantity – it is simply there to make the left-bound bases and exponents appear fixed, so that the essential pattern of the Goodstein sequence itself can be made more plain. In other words, again, there is no need to rely on the concept of finitized infinity to prove the Goodstein result, and doing so only creates confusion. Another way of saying all this is that the Goodstein argument (and the Goodstein theorem that results from it) is not an example of the usefulness or validity of the concept of finitized infinity, i.e., of what the ω symbol represents in set theory, despite claims to the contrary. It will always be the case that if a question or problem is based on logically valid definitions and assumptions, there will not be a need to invoke the concept of finitized infinity, or any other logically flawed concept, in order to answer the question or solve the problem.
One way of understanding why the standard Goodstein argument seems to work and to be right, and yet at the same time seems to have a certain intrinsic nebulosity – other than to say that it involves the finitizing of the infinite, which we have already discussed – is that the argument relies not on a clear deductive path to draw its conclusion, but on a tug-of-war between two sets of ideas that have been overlain in inappropriate ways, each of which serves as necessary scaffolding at each step of the sequence at the particular point where the part of the argument made using the other fails. In this way, the argument seems to be valid, because the limitations in each set of ideas with respect to the other are made up for by the other. At each step in the pair of sequences, the fact that the Goodstein number for that step is actually generated and put in CNF before ω is finally brought in as the last part of the process to replace n+1 ensures that the “strictly decreasing” ordinal sequence remains in sync with the Goodstein sequence at every step, even though what is being replaced by ω increases by 1 at every step and so it is not correct to say that the “value” of the ordinal sequence expression has been reduced at that step. But what this does is ensure that even though we incorrectly say that the ordinal sequence is “strictly decreasing,” the ordinal sequence can still be an accurate representation of the Goodstein sequence itself, and it is therefore still justified to say that when the former reaches 0, so does the latter. On the other hand, if we say that the ordinal sequence is nothing but a disguised copy of the Goodstein sequence, and therefore it is not correct to say that the ordinal sequence is strictly decreasing, one may point to the fact that the expressions in the ordinal sequence themselves are easily-understood polynomial expressions, and since ω always remains the same or becomes a finite number that inevitably reduces, and since we are (presumably) reducing by at least 1 at every step, then how can we not say that the ordinal sequence is strictly decreasing? This back-and-forth between two simultaneously competing and mutually supportive sets of ideas makes it more difficult to sort things out fully and clearly. But the reason the ordinal sequence seems to be strictly decreasing is not that it actually is, but that (a) we never work out in sufficient detail a proof of this strict decrease but simply assume that what we see in the first few polynomial expressions of the ordinal sequence must apply to all subsequent expressions, and (b) we have once again conflated two different but, in certain ways, related concepts and are treating them as equal; in this case, two different meanings of equality itself. In saying that the ordinal sequence is strictly decreasing, we are saying that each element in the sequence is a number, and that the number at a given step is always less than the number at the previous step; if the elements in the ordinal sequence are not treated as numbers, it makes no sense to say that there is any decrease (or any kind of numerical change) happening between steps. But this means that the ω symbols themselves must be treated as numbers, and given the nature of the Goodstein argument, if they are treated as numbers then they can be treated as nothing other than the same number across all steps. However, if this is to be the case, then we may easily find counterexamples to show that there is no guarantee that any given ordinal sequence is strictly decreasing, as we did for ordinal sequence 11 earlier in this section. The implication, then, in the Goodstein argument that the elements in the ordinal sequences are polynomial expressions in which ω represents a fixed quantity across steps and whose values always decrease across steps in a given ordinal sequence, or can be made to always decrease across steps with a large enough constant for ω, is in actuality not a conclusion that the standard Goodstein argument has enough information to legitimately draw. The reason all ordinal sequences eventually reach 0 is not that they are strictly decreasing, but that, as explained above, the Goodstein sequences themselves always eventually reaches 0, and the ordinal sequences’ elements are kept in lockstep with their corresponding Goodstein sequences’ elements the entire time. When we say that the ordinal sequence is strictly decreasing, we are confusing something that is cyclical or repetitive across steps, viz., the use of ω in every expression at every step (except the last stretch, which is typically not considered in a recounting of the Goodstein proof) in, for the most part, the same terms in the same coefficient and exponent relations, with numerical equality. Both can be considered types of “equality,” in that the former repeats the process of using ω in the same spots over and over across steps, and the latter is the standard mathematical equality of numbers. But the algebraic relations in which the ω symbols are placed, combined with an (incorrect) belief that even though ω represents infinity, it can still be treated as a finite number which can be added, multiplied, raised to a power, etc., makes us conflate these two different types of equality, and treat them as if they were the same. The former type of equality, though, does not represent mathematical equality, but the equality of a placeholder, a single symbol that is used to hold the place of whatever number or numbers are in the particular spots in which it is used; as such, this type of equality does not guarantee that the numbers being replaced by the placeholder symbol are the same numerical value across steps, and it is thus entirely consistent with this type of equality for the numbers which are replaced by the placeholder symbol to be different across steps, and, in particular, different in a way that sees the values in the ordinal sequence increase or remain the same across steps rather than decrease. By understanding that we are conflating two different, but in certain ways similar, things, we can start to tease them apart, and it is this teasing apart of conflated concepts that is the beginning of greater clarity.
The standard Goodstein argument is a quasi-conflation of valid and invalid concepts that are superficially similar to each other in enough relevant ways and that have been conceptually massaged against each other often enough and with enough pressure in the right places that the dissimilarities and incongruities that exist and remain within it no longer frustrate and bewilder, as they should, but, as with the diagonal argument, paradoxically serve as markers of how far we have come in our understanding of things, as battle scars of our mathematical maturity. We have found the kind of result we wished to find, viz., a result which shows the supposed mathematical validity and efficacy of the ideas we have spawned to finitize infinity. As stated, there is only one way in which the Goodstein argument can be made which is logically valid, and that is by using ω as a placeholder for n+1 at every step in order to more clearly see the pattern in the Goodstein sequence itself, and this way does not allow for ω to be used to represent infinity, or a fixed quantity, or a quantity which reduces across steps, and it does not allow us to conclude that the ordinal sequence strictly decreases, because a placeholder object is not a value or number, and as such, expressions that combine a placeholder symbol with arithmetic operators are not numerically or mathematically meaningful, which, in turn, means that one may not “reduce” the “value” of one such expression to the “value” of another. In other words, the only valid way to make the Goodstein argument is also, not coincidentally, a way which does not make use of the concept of finitized infinity. This should be expected, since finitized infinity is a logically flawed concept.
This is an older result from 1922 that discusses models of set theory in first-order predicate logic. Today, set theorists and logicians widely regard it as not an actual paradox like Russell’s paradox, but as something that has certain paradox-like elements or that can seem like a paradox from certain angles.88 We will not discuss Skolem’s paradox in detail, but will only make a specific comment. Skolem’s paradox says that in a certain countable model B of Zermelo’s axioms “there is some set u in B such that B satisfies the first-order formula saying that u is uncountable.”89 In other words, in this model of set theory, which, if it is to be an accurate model must include mention in some form of uncountability, since uncountable sets are a standard part of set theory, there are statements that say that there are sets, such as u, which contain an uncountable number of elements. But since the model B is countable, meaning “there are only countably many elements … in B to begin with,”90 how is it then possible for B to contain an uncountable set? Presumably such a set would need to contain more elements than B contains in its entirety, which is impossible. But “Skolem went on to explain why there was no contradiction. In the context of a specific model of set theory, the term ‘set’ does not refer to an arbitrary set, but only to a set that is actually included in the model. The definition of countability requires that a certain one-to-one correspondence, which is itself a set, must exist. Thus it is possible to recognise that a particular set u is countable, but not countable in a particular model of set theory, because there is no set in the model that gives a one-to-one correspondence between u and the natural numbers in that model.”91 In other words, a set in a given model of set theory can be defined to be uncountable simply by not explicitly including an actual set in the model that shows its one-to-one correspondence with the natural numbers. But then, have we really been able to model uncountability by this means? As with concluding that CH is true on the assumption that CH is true, if there are explicit idiosyncratic defining traits in a particular model of set theory for the word “uncountable,” and we explicitly tweak a particular set’s definition so that it matches these traits, then of course in this countable model of set theory we may say that “this particular set is uncountable.” But this does not help us understand uncountability. It is like saying that a brick is made of smaller bricks: it pretends to be an explanation, and superficially it may hit the ear like an explanation, but actually it explains nothing. Sound and fury. Further, we are told that “it is now known that Skolem's paradox is unique to first-order logic; if set theory is studied using higher-order logic with full semantics, then it does not have any countable models, due to the semantics being used.”92 Also, we are told that “Kleene (1967) describes the result as ‘not a paradox in the sense of outright contradiction, but rather a kind of anomaly’. After surveying Skolem's argument that the result is not contradictory, Kleene concludes: ‘there is no absolute notion of countability’. Hunter (1971) describes the contradiction as ‘hardly even a paradox’.”93 Without reading the original sources of these quotes, we cannot be sure of their full conceptual context. However, the meaning of each does seem reasonably clear, so we will proceed to analyze these conclusions in light of what we have said so far in this paper.
First, Kleene describes the paradox as an “anomaly.” But if something is or seems anomalous, this means we do not fully understand it. A full understanding of something eliminates all anomalies. Hunter describes it as “hardly even a paradox.” This, too, stops short before a full explanation is reached. Really, what Hunter does here is to diminish the significance of a problem that he does not know how to resolve in a satisfactory way. Kleene’s and Hunter’s view is widely shared: “Current mathematical logicians do not view Skolem's paradox as any sort of fatal flaw in set theory.”94 In other words, practitioners acknowledge that “something” is anomalous regarding Skolem’s paradox, and therefore that “something” here is not fully explained, but whatever it is, it is deemed to be insignificant. Regarding Kleene’s comment that “there is no absolute notion of countability,” it seems reasonable to say that his conclusion was related to absolute vs. relative properties of various different models of set theory in first-order logic: “Skolem used the term ‘relative’ to describe this state of affairs, where the same set is included in two models of set theory [and] is countable in one model and not countable in the other model. He described this as the ‘most important’ result in his paper. Contemporary set theorists describe concepts that do not depend on the choice of a transitive model as absolute. From their point of view, Skolem's paradox simply shows that countability is not an absolute property in first-order logic.”95 However, this does not provide a reason why countability is not an “absolute” property.
But the resolution to this anomaly should be clear. The concept of “uncountable” infinity is logically invalid, because the first “level” of infinity is never finished, and, therefore, a second, higher level can never begin. There is only one level of infinity. The reason countable models such as Skolem’s above cannot properly model uncountability is that uncountability is an illogical, and thus un-modelable, concept; thus, as with CH, the opaqueness and intractability of this “anomaly” persist, despite all efforts to make things clear. We do everything we can to reduce the significance of this anomaly in our minds, and in our mathematical and philosophical discussions, to sweep it under the rug, because we simply cannot think of a satisfactory way to eliminate it. But the reason for our inability to understand the source of the anomaly is that we are analyzing the anomaly in the context of ideas that are based on flawed assumptions, and which assumptions have direct relevance to the anomaly. Understand the flaw in the assumptions, and we understand, and thereby eliminate, the anomaly. We should also note that the anomaly is not resolved by simply modeling set theory in second-order or higher-order predicate logic. In higher-order logic, we can quantify over not just individuals, but sets of these individuals, and sets of sets of these individuals, etc. Higher-order logic, for example, “admits categorical axiomatizations of the natural numbers, and of the real numbers, which are impossible with first-order logic.”96 In particular, at a given logic level we may quantify over the power set of the elements quantified over at the previous level, and so, in the standard understanding, where we could not talk about properties of the natural numbers as a whole or of the real numbers (which as we understand from standard set theory have a cardinality that is equal to that of the power set of the natural numbers) as a whole, or quantify over uncountable sets, in first-order logic, we can do so in higher-order logic. But note that this ability is part of the definition of higher-order logic. There is nothing in higher-order logic that confirms or proves that there are different levels of infinity, or that uncountable sets exist. In higher-order logic, it is assumed that these things are true, e.g., that it is possible to take the power set of a completed infinite set and produce another completed, uncountable infinite set, or that it is possible to raise a finite (or infinite) number to an infinite power and produce a meaningful result. As with cardinal and ordinal arithmetic, once we assume that such logically contradictory things are possible, it becomes a comparatively easy matter to develop a theory, a set of ideas, symbols, properties, relations, etc., that is founded on these assumptions. The reason Skolem’s paradox has persisted for so long, despite our best efforts to make it seem trivial, is that the paradox directly addresses the relationship between countable and uncountable infinity, by requiring that we try to understand the nature of an uncountable set being modeled in a countable model. This is the same reason CH and generalized CH have stood the test of time for so long and have, at an essential level, remained inscrutable: in each case, Skolem’s paradox and CH, the question cannot be addressed or answered in the context of the common or standard assumptions the way typical questions of mathematics and mathematical logic can; rather, each question is about the very nature of a logically flawed assumption itself, and thus directly bear upon the assumption, forcing us to dig deeper than we are used to digging, or than we might wish to dig, and forcing us, eventually, to come to terms with certain basic flaws in our reasoning. But the process of coming to terms with such flaws is a necessary part of the larger, longer-term effort of adjusting the individual, and the collective (to the extent possible), human psyche to the light of a sober, objective view of reality.
The assumption that this is true is known as the axiom of constructibility in set theory. It is not an axiom that is part of the standard version of set theory, but various practitioners have chosen to include it for various reasons in their version of set theory, or in a version they have decided to study. Here V represents all sets, i.e., the universe of sets, and L represents all constructible sets, which is a characteristic that is not as easily defined as it might seem, but we may say that L consists of sets whose elements can be explicitly laid out or whose pattern of generation can be explicitly determined, and which therefore can be constructed. This is opposed to other sets that are allowed in standard set theory in which such a set’s elements or its elements’ pattern of generation cannot be explicitly laid out or determined, i.e., the set is one which we cannot explicitly construct, but whose existence is nonetheless affirmed, such as sets that “must” exist because it is logically impossible, in the context of the axioms and prior results of standard set theory, for them not to exist, which means that the assumption of their nonexistence leads to a logical contradiction in the context of these axioms and prior results. Such sets do not have to be explicitly constructed or generatable by a known pattern for a non-constructivist to conclude from such a reductio ad absurdum proof that they exist. A constructivist, however, would not find such an argument convincing, and would demand that the set that is presumed to exist be explicitly constructed, either directly or indirectly, before he will accept the set’s existence. The question, then, asks whether or not all sets are constructible, i.e., whether it is permitted in set theory to say that there can be sets that exist in the universe of sets but that cannot be explicitly constructed and whose pattern of construction cannot be explicitly determined.
According to the above definition, the answer must be yes, all sets are constructible, since sets whose elements can be explicitly laid out or whose pattern of generation is at least knowable, if not necessarily known at a given moment, are all the sets that can be logically constructed, i.e., whose definitions do not contain a logical contradiction; even from a reductio ad absurdum proof which does not give us the elements in a set or the set’s pattern of generation, if the set is able to logicallygf exist, i.e., if there are no contradictions in its definition, either directly or indirectly, then the set is knowable, i.e., capable of being intuitively understood, even though we do not yet have knowledge of the elements in it or how the elements are generated. The only reason a reductio ad absurdum proof would be a reason to question the existence of a set that the proof says must exist is if the axioms and prior results upon which the proof is based, or the logic of the proof itself, already contained a contradictory concept, such as that of finitized infinity or uncountable infinity, or any other logical flaw. If the axioms, prior results, and proof logic are without logical flaw, then the set that the proof says must exist is a logically valid conception, and therefore must be intuitively understandable; from that point it would only be a matter of searching for the elements of the set or their pattern of generation. But matters become more convoluted when we factor in that there are multiple, partly overlapping and partly contradictory, definitions from different practitioners for “constructible,” and especially when a given definition includes the concept of the transfinite or uncountability. In the context of these various definitions, the question cannot be given a definitive or objective answer. The answer depends on the way one defines “set” as well, and in fact, the question of whether V = L can be thought of as an effort to try to alter or adjust one or both of these definitions in such a way that the two can be made equivalent, and if this cannot be done in an agreed-upon or satisfactory way by all practitioners, perhaps after a sufficient number of years or decades of trying, then perhaps it can be concluded that V ≠ L after all. In other words, to a certain extent there is arbitrariness involved in this question, although as discussed above, as well as in the section below on the universe of sets, if we eliminate the logically flawed conceptions from set theory then a clear and satisfactory answer to this question can be obtained, by properly defining “set” and properly defining “constructible.” However, our purpose here is not to dig into the philosophical underpinnings of the question of what a “set” actually is. Instead, we will discuss here why some set theorists and philosophers have felt the need to define sets in a “constructible” way in the first place, since this bears upon the topic of this paper.
Simply put, forcing sets to be explicitly constructed is a way to try to obtain as much certainty as possible about the nature of the universe of sets, so that one can eliminate as many unknowns and paradoxes, and as much potential for contradiction, flaw, misconception, and confusion, as possible. In this way, we hope to find the “true” nature of sets, or at least to define such a nature more unambiguously, completely, and satisfactorily. But it is the confusion of ideas which springs from implicit, unacknowledged logical error that is a significant motivation to create a constructible universe of sets, since such logical errors hinder progress toward clear understanding in various subtle ways by producing blind spots and blind alleys, impossible results or paradoxes, persistent opaqueness and intractability, and consistent lack of ability among practitioners to agree on foundational things. Understand what and where the logical errors are, and we clear up the confusion and reduce the need to say that all sets must be “constructible.”
But to the extent that the concept of constructibility has value for helping us understand sets, or understand the world, this value can be marred by the same logical errors that its defenders try so hard to eliminate by forcing everything to be constructible. For example, if we assume that the constructible universe can contain countable, much less uncountable, instances of finitized infinity, then we have explicitly negated the meaning and value of the concept of constructibility, even though we may still call such sets “constructible” by a suitable redefinition of “constructible.” As soon as we start including in our constructible universe the idea of finitized infinity, so that completed infinite sets can be mathematically manipulated and lined up in order of magnitude as if they were finite, fixed quantities, or so that uncountable sets can “be constructed,” we have made the logical mistake of conflating the finite with the infinite within the constructible universe and have thus undermined our own effort at eliminating logical errors by restricting ourselves to the “construction” process to create sets. Gödel does this, for example, in his 1938 paper “The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis.”97 In this paper, Gödel takes as a starting point a certain version of set theory and then proposes to prove that four additional axioms beyond this are consistent with this version of set theory; and that, furthermore, he is able to make this proof in a constructible way, so that if no contradictions are “obtained in the enlarged system,” then we can be certain that there are no contradictions in the extended set of axioms, and thus that these axioms are all mutually consistent. But then Gödel defines constructible, as he uses the term in his paper, in the following way: “‘constructible’ sets are defined to be those sets which can be obtained by Russell’s ramified hierarchy of types, if extended to include transfinite orders.” (Italics mine.) He then goes on to discuss uncountable infinity in the context of his “proposition 2,” which in his list of four additional axioms is the one that says that generalized CH is true: “From [the assumption that every set is constructible] the propositions 1-4 can be deduced. In particular, proposition 2 follows from the fact that all constructible sets of integers are obtained already for orders < ω1, all constructible sets of sets of integers for orders < ω2 and so on.” His method of proof is to construct a model of set theory that assumes that the initial set theory plus the four additional axioms are all true, and then look for any contradictions; if there are no contradictions, then it can be concluded that the axioms of this extended version of set theory are mutually consistent, and further, that they are all consistent with the axiom of constructibility as he has defined it. In particular, generalized CH would be consistent with the axiom of constructibility.
But Gödel places a strong limit on the strength of the result. In a footnote, he states “that the model [which he constructs that includes the initial set theory plus the four additional axioms] is constructed by essentially transfinite methods and hence gives only a relative proof of consistency, requiring the consistency of [the initial set theory] as a hypothesis.” (Italics mine.) In these comments we can see that Gödel relies for his proof on the assumption that the transfinite exists. We also see a statement of the fact that he is not proving that generalized CH is true, but rather that if the axioms of his initial set theory are mutually consistent, then generalized CH is consistent with them, i.e., that there is nothing in the possible deductions or results from the initial set theory extended into the transfinite that can say that generalized CH is false. We will not address the details of Gödel’s proof here. We will just note the fact that any proof based on the assumption that the transfinite exists, or that there are different levels of infinity, is based on the logical flaw of conflating the finite with the infinite, and thus will produce erroneous results from the perspective of reality, that is of contextless logical necessity. Any such proof may seem valid in the context of axioms and assumptions that already assume as valid the logical flaw of conflating the finite with the infinite, so long as the agreed-upon conventions and equivalences and methods of proof in use in that context are strictly followed. But it is important to distinguish truth that is relative to a particular (possibly flawed) context from truth that is logically necessary and therefore must be valid in all (logically valid) contexts. The conclusion that generalized CH is not provable or disprovable on the basis of the axioms of ZFC, if we limit choice to countable choice, is correct, but this is not because generalized CH must simply require certain other unknown axioms before it can be seen to be correct or not. It is because CH and generalized CH are not meaningful statements at all, from the perspective of truth that does not depend on context, because the entities discussed in these hypotheses are not things that correspond in any way to anything that is in or could exist in the real world, even conceptually. And if we do not separate contextual and non-contextual truth from each other, progress will be slowed, and beyond a certain point impossible. This also means that the conclusion that generalized CH is not provable or disprovable on the basis of the axioms of ZFC when these are extended to the transfinite is a logically meaningless conclusion, because it purports to draw a logically valid conclusion on the basis of logically flawed assumptions, which is impossible.
Is the axiom of constructibility consistent with generalized CH? This question cannot be properly answered. According to Gödel, it is, because he can build a constructible model that extends standard set theory to the transfinite and includes generalized CH without contradiction. But for two statements to be consistent, they both have to be logically meaningful, so that we can conceive in a logically valid, and thus intuitive, way that the logical consequences of either statement cannot produce a contradiction of the other, and this requirement is lacking in Gödel’s proof, which makes use of logically invalid, and thus meaningless, concepts to draw its conclusion. But also, as in Skolem’s paradox and the different idiosyncratic ways in which “uncountable” is defined in different models, such a “constructible proof” depends crucially on how “generalized CH” and “consistent with generalized CH” are defined in a particular constructible model, as well as how “constructible” is defined; and a “precise” definition within the model does not mean precision with regard to logical comprehensibility of the concept. Because constructibility is an idea that is used to try to eliminate flaws, errors, misconceptions, vagueness, etc., in the study of set theory and its foundations, it is important to realize that though we may say that the axiom of constructibility, appropriately defined, is “consistent” with generalized CH, this does not eliminate the flaws, errors, misconceptions, etc., with regard to CH or generalized CH itself, as these hypotheses are still based on the logical error of conflating the finite with the infinite. Neither CH nor generalized CH is proven correct by generalized CH being consistent, in an appropriately-defined sense, with the axiom of constructibility, and neither are CH and generalized CH brought closer, in a mathematical sense, to being proven or disproven by such a proof of consistency. The consistency proof, on the one hand, and the determination of the nature, meaning, and logical status of CH or generalized CH, on the other, are separate things. If an argument regarding the status or meaning of CH or generalized CH does not address the logical error of conflating the finite and the infinite, then it does not address the root of the CH problem, and so it does not in any way answer the CH question; at most, it serves as another independent result which adds fuel to the idea that CH cannot be solved by traditional means.
But if, as we have said in the previous paragraph, Gödel’s consistency conclusion is based on logically flawed premises, and cannot thus be considered a legitimately logical conclusion, why did Gödel believe it was? And why does nearly every set theorist also believe this? The broader conceptual context certainly plays a part – the supposed unassailability of the diagonal argument, and the hero-like status that Cantor holds among set theorists because of it; Gödel’s remarkable incompleteness proofs and his hero-like status that results in part from these; the significance of the consistency result itself, in relation to what it means for CH; the fact that the consistency result has been widely accepted now for decades, which adds an air of veneration to it that it would not otherwise have; and any number of other factors. But the point to be made here is different from these. When we “extend” various process and operations that are valid in the realm of the finite into the realm of the infinite, there comes a point, as discussed elsewhere in this paper, when the infinite “quantities” that we are dealing with lose their essential quality of being infinite, in that they are treated in various essential ways as if they were finite entities – we perform mathematical induction and recursion on them, we add and multiply them and raise them to various powers or treat them as exponents, we line them up in order of magnitude, we apply theorems such as Cantor’s theorem about the cardinality of a set’s power set to them, etc. But when we do this, we make it so that the conclusions we draw with regard to these infinite “quantities” become, more or less, precisely the conclusions and types of conclusions which can be drawn with regard to actually finite quantities. And this makes sense, because we wish to understand infinity, but since the only way to logically understand quantity and relations between quantities is if the quantities involved are finite, the only possible way to “understand” the transfinite is to treat transfinite “quantities” as if they were, in essential ways, finite quantities. And so, unsurprisingly, this is what we have done. But in doing this, in finitizing infinity so that we may feel that we understand it, we ensure that our understanding of the transfinite excludes the types of conceptions that might be used to help resolve CH. CH relates countable to uncountable infinity, but by making the effort to finitize infinity so that we may feel we understand the transfinite, and thus by, in essential ways, bringing the transfinite into the realm of the finite, we strip our conception of the transfinite of any ability to make statements about the uncountable, and thus about CH. But making something understandable, that is, logically comprehensible, means to purposely work to remove all ideas that are logically flawed, and since the concept of uncountable infinity is logically flawed, it is not surprising that an effort to make the transfinite logically comprehensible also strips our conception of the transfinite of the ability to say anything meaningful about uncountability. In other words, it is not surprising that Gödel concluded that generalized CH is consistent with his extension of the axioms of ZFC into the transfinite – consistency in this case means that no result based solely on this extension can be used to disprove generalized CH. But the more we treat the transfinite like we treat the finite, the harder it is for our conception of the transfinite to say anything at all about logically flawed concepts such as uncountability. The fact that the transfinite includes instances of uncountable infinity is irrelevant, because, again, we treat these instances in essential ways as if they were finite, in order to feel as if we are able to make progress in understanding them. The consistency proof, then, is not so much a proof of consistency, which implies that all conceptions involved are logically sound, if not necessarily arranged in mutually consistent ways, as it is an indirect and skewed illustration of the fact that the more we try to bring logically flawed concepts into the realm of the understandable, by decorating or overlaying them, so to speak, with logically valid concepts and placing them into logically valid arrangements, the less room we have for the logically flawed concepts themselves to continue being part of the picture. It may seem then, at least in a sense, that we hinder our own efforts to resolve CH by making the transfinite as much like the finite as we can. But the reality is that the effort to make our understanding of number and quantity logically comprehensible, if followed through with, will ensure that we do resolve CH, by showing that CH is based on logically flawed concepts, and is thus a meaningless statement; and that we actually hinder our efforts by going in the opposite direction, viz., by trying to more directly incorporate the flawed concept of uncountability into our ideas and formalisms, e.g., through the means of adding various conceptual primitives or axioms to our framework which if arranged or used in deductive paths in the right ways would be able to help logically or definitively prove various statements about uncountable infinity, including whether or not CH is true, and thereby help us intuitively understand uncountable infinity. The more we take this latter path, the more layers of confusion we add, and the harder it becomes to dig ourselves back to the surface.
We are told in Hrbacek that the axiom of infinity states that “an inductive set exists.”98 An inductive set can be defined as a set that can be placed into a one-to-one correspondence with the natural numbers and whose elements can be produced by taking the natural numbers into a function one after another in sequence in order to produce each successive element of the set, and so such a set can be considered to have an infinite number of elements. Another way of defining “an inductive set” is simply that it is the set of natural numbers itself, in which case the axiom of infinity would be postulating that the set of natural numbers forms a completed entity. Yet another way of interpreting this axiom is to say that it is legitimate to assume that completed countably infinite sets which can be produced by an explicit and easily identifiable pattern exist. They state further that
Some mathematicians object to the Axiom of Infinity on the grounds that a collection of objects produced by an infinite process (such as ℕ) should not be treated as a completed entity. However, most people with some mathematical training have no difficulty visualizing the collection of natural numbers in that way. Infinite sets are basic tools of modern mathematics and the essence of set theory. No contradiction resulting from their use has ever been discovered in spite of the enormous body of research founded on them. Therefore, we treat the Axiom of Infinity on a par with our other axioms.99
Of course, they rightly treat this statement as an axiom, i.e., a statement that they assume to be true without any definitive proof. But the need to treat this statement as an axiom in the first place is the result of confusion regarding what exactly an infinite set is, or is supposed to be. The mathematicians who object to the axiom of infinity on the ground that it is impossible to collect an infinite number of elements into a finite entity that can be manipulated as a whole in various ways as if it were a finite, i.e., completed, thing, do make a valid point, i.e., that it is a logical error to conflate the finite and the infinite. But then, how do we square this with, as Hrbacek state, the fact that the assumption of the existence of (countably) infinite sets has not led to a contradiction despite an enormous body of mathematical results that are dependent on this assumption, or the fact that it is quite easy for someone with a little mathematical training to clearly conceive of such infinite sets? But we have discussed this already in previous sections. This debate rests on the treating of an infinity as if it were finite, i.e., equating an infinity with a finite thing, and then concluding that we are talking about one thing, viz., “an” infinite set, when actually we are talking about two things. The pattern that produces the elements of the infinite set is finite and simple, and thus easy to understand. The sequence of elements produced by this finite pattern, however, is infinite, because no matter how many times this finite pattern is applied, it can always be applied again. In our effort to try to reduce as much as possible to formulas that we can circumscribe and manipulate, and to try to find as many connections and general patterns as possible between and among mathematical ideas, it is easy to gloss over this essential difference and conclude that the infinite sequence of natural numbers is the finite pattern that produces them, and it is certainly mathematically convenient to do this. We then grow accustomed to thinking of these two things, one finite and the other infinite, as if they were the same thing, and forget that the equating of these two things that we have done is in actuality nothing more than a practical conceptual tool that aids in visualizing and conceptualizing certain mathematical ideas and processes. But, as with any practical tool, this one also has its bounds of applicability. This equating of the finite with the infinite does not cause problems in many areas of mathematics because in such areas and investigations we may safely gloss over the essential logical error in conflating the finite with the infinite, and this, in turn, is because such investigations only require an approximation of the full truth with regard to the infinite set in question. But, in areas of investigation which bear more directly upon the nature and meaning of the logical error, this approximation is no longer sufficient, because we are now forced to face the logical error squarely; i.e., we have breached the bounds of applicability of the practical conceptual tool that has been sufficient and useful up to this point. Learning to tease apart these two things, the pattern that can be used to produce an infinite sequence of elements and the infinite sequence of elements itself, requires unorthodox thinking, because we have equated these two things so thoroughly and for so long that it can seem like a sacrilege to unequate them. But if we do unequate them, i.e., if we recognize the logical error inherent in equating the finite with the infinite, then we can resolve this debate regarding the axiom of infinity – an infinite sequence of elements can never be collected into a finite entity, because this would be a violation of the meaning of the word “infinite”; but it is still meaningful and mathematically useful to say that a finite pattern can produce as many elements of an infinite sequence as we like, and that really what we are considering in these various branches of mathematics in which such sets find use, and in which such use does not entail contradiction, is not a finished collection of an infinite number of elements, but the pattern that produces these elements, which is clearly conceived, along with, at any given time, a finite subset of these elements. This distinction is one that is not relevant for much of mathematics, but for certain foundational problems, such as CH, it is essential to ferret it out and understand it. But then, once we know the nature of this logical error, we are able to see how to correct other problems that, in one way or another, are founded upon or related to it, even if the solving of these other problems was not the initial reason for our investigations.
It is telling that Hrbacek use as justification for including the axiom of infinity in their list of valid axioms the fact that “no contradiction resulting from [the use of infinite sets which are allowed for by the axiom of infinity] has ever been discovered” in all of mathematics that have made use of the axiom. They do not say that there is a specific, logically necessary reason why the axiom of infinity must be true. They rely on the fact that the “experimental data,” so to speak, strongly indicate that the axiom is true, which is, of course, short of definitive knowledge. They rightly, therefore, call the axiom of infinity an axiom, i.e., a statement that is assumed true without proof. But one may go further than this standard “all conclusions are tentative no matter how much data is gathered and how confident we are that we are correct” scientific approach to knowledge when one’s investigations concern inherent logical structure; this is not the case with typical scientific investigations, in which we depend for our conclusions on the gathering of data, and in which it is always possible, at least in nontrivial systems, and in a certain way in trivial systems as well, that we have not gathered all of the appropriate data about something, or analyzed the data in the right ways, in order for us to be able to conclude definitively that what we think we know about that something is in fact the truth about it (though I will note, without elaboration at this time, that even here there is some leeway). But in the realm of investigation whose subject matter is the nature of logical necessity, once we understand a logically necessary truth, we know it to be true, and no further proof or data gathering is needed to help strengthen a tentative acceptance of its validity; though the gathering of additional data can help illustrate this validity in a fuller way, and can help us see connections to other logically necessary truths. (This also will be counterintuitive to many. We will not discuss the justifications for this further in the paper, leaving these for future works; in any case, a detailed discussion of these justifications is not necessary to understand the conclusions in this section regarding the axiom of infinity.) In relation to the axiom of infinity we may make matters definitive, rather than provisional, which is how they currently stand in set theory, by simply acknowledging the existence in modern set theory of the logical error of conflating the finite with the infinite, and separating, as two different but related things, the finite pattern that can generate an infinite sequence of elements from the infinite sequence of elements so generated. On this basis, we may then change the axiom of infinity so that it states something along the lines of, “A finite pattern can produce an infinite sequence of elements, which cannot be completed but which, as a practical convenience, we may call an infinite set.” This is a more honest statement about the relationship between the finite and the infinite than is the current axiom of infinity. Furthermore, we can clearly see that it is true, and that it does not in any way leave us with the feeling that something about the nature of infinity is just missing from the axiom, an axiom which, as its name implies, might be expected to help us achieve some degree of clarity about the nature of infinity, rather than to leave out what seems to be certain hard-to-define crucial elements that would give us a genuine or definitive reason to believe that the axiom is true. Our alterations to the axiom of infinity, in other words, result in a statement that does not leave us with any doubt about its logical status or with any lack of clarity regarding what it means, and at the same time does not in any way affect or alter the meaning of or attempt to invalidate any logically valid mathematical results that are based on the assumption of the existence of countably infinite sets. In fact, our new statement is consistent with all such results. The only difference between the original axiom and our restatement is that the restatement clarifies the relationship between the finite and the infinite so that we can clearly see what the relationship is. And ultimately, the “axioms” on which we base our thought about the logical structure of reality must be logically valid themselves, if they are to help give us an accurate understanding of reality’s foundations. In other words, set theory and its foundational conceptions must be modified in certain ways if set theory is to be a fully accurate foundation, or part of such a foundation, for our understanding of the basic framework of the world.
First let us consider the union of two countable sets. We will take as these two sets the odd and the even natural numbers. The odds, 1, 3, 5, 7, … are an infinite set, because this sequence never ends. The evens, 2, 4, 6, 8, … are also infinite. Yet if we line them up and alternate them in a linear sequence, the first element from the first set, then the first element from the second set, then the next element from the first set, etc., the sequence can be placed in one-to-one correspondence with the natural numbers, and thus the union of these two countable sets must itself be countable. But how could this be possible if the two original sets were completed entities? In general, how is it possible for two sets, each with its own elements, to combine in a union and the union have the same number of elements as one or both of the original two sets? But this kind of situation can only arise if at least one of the two sets being unioned (in this case both of them) is not a completed entity after all, i.e., if it is unjustified logically to treat one or more of the sets involved as being “completed” or “finite.”100 Rather, as per the previous section, it is the pattern that generates these elements that is finite, and that we have, for convenience, equated to the infinite sequence of elements, but which is, in fact, logically distinct from it. In the case of this example, both original sets extend forever, i.e., each set increases in number of elements without bound, and so since we are placing the alternating linear sequence of the union of these two sets (or any combined arrangement of their elements – they do not have to be arranged in a strict alternating fashion between the two original sets) in one-to-one correspondence with a sequence, the natural numbers, that itself also never ends, then no matter how many of the elements of the original two sets are added to their growing union, there will always be additional elements available in the corresponding infinite index sequence to correspond one-to-one with the additional elements in the union. The fact that the union of two countable sets, or, by induction, n countable sets, where n∈ℕ, is a countable set, can be understood simply by the fact that infinity is infinite, and can therefore accommodate any number of elements that are added to a union of sets, no matter how many elements are added or how many sets are unioned. And in the cases mentioned so far, it is accepted that this is possible in ZF alone because so far we are only talking about a finite list of sets, each either finite or countable, that we are unioning, and so it is clearly understood how we may aggregate the elements from the various sets being unioned into one combined set. In other words, it is understood how we may fully circumscribe, i.e., make finite, the list of choices we must make in determining the elements from each set to add to the combined set in a given round of the choice process, so that we can feel that we are guaranteed to get every element of all the original sets into the combined set. To state it yet another way, we are able, with a finite list of finite or countable (or both) sets, to perceive a pattern, which we can see how to repeat over and over as many times as we like, with each iteration of this pattern passing once over all the sets being unioned; and then since a finite pattern, or algorithm, can be applied any number of times we wish, and since each application of the pattern produces, as part of the unioned set, a finite number of elements, it is easy to see how the iterations of this pattern can be mapped one-to-one with the natural numbers; and we may then line up the finite list of numbers produced by each iteration of the pattern with the natural numbers as well, and since the natural numbers never end, the succession of these finite lists, and their individual elements, can be mapped one-to-one with the natural numbers for as long as we like. We should note here again that in modern set theory it is not felt that an “axiom of choice” must be added to the other ZF axioms in order to understand this process or to feel as if we know that it is logically valid.
But it is different with countable unions, either of finite or countable sets (or both). This is recognized in set theory, but the full meaning of the difference is not clearly perceived. Hrbacek state that because “the union of a finite system of countable sets is countable … one might be tempted to conclude that the union of a countable system of countable sets is countable. However, this can be proved only if one uses the Axiom of Choice … . Without the Axiom of Choice, one cannot even prove the … ‘evident’ theorem” that the union of a countable collection of sets each of magnitude 2 is countable.101 It does seem evident that we should be able to create a single infinite set out of all the elements of these two-element sets, by, for example, lining up the two-element sets one after the other and then, for each two-element set, taking one element from it and then the other, placing both as elements into a single new, combined set. In this way, we may continue adding elements two at a time to this combined set for as long as we like. In fact, there is nothing wrong with doing this, and it is a perfectly valid, logically sound procedure to create the union of these two-element sets. The problem that modern set theory has with this is based on its idiosyncratic way of constructing unions, and the difficulty of finding a satisfactory resolution to this issue is exacerbated by a misunderstanding of infinity.
Specifically, Hrbacek tell us that “the difficulty is in choosing for each n∈ℕ a unique sequence enumerating [the two-element set corresponding to n]. If such a choice can be made, the result holds … .”102 But why should such a choice be difficult to make? The authors do not make it clear why it is difficult to choose a “unique” sequence for a given set. Each two-element set has two elements, i.e., a finite number of elements. Why does it matter which of these is chosen first and which second in the process of adding elements to the union set? It is clear, as spelled out in the previous paragraph, that regardless of which element is chosen first, both elements in a given set can be added to the union set in a finite number of steps, in this case two, and that this process is clearly understandable and logically valid and can be repeated for as many of the two-element sets as we like. The same is true for the countable union of sets of any finite magnitude. In fact, the difficulty in (or ease of) choosing elements from each set being unioned is no greater or less in the case of finite collections of sets than in the case of countable collections of sets; if we have a problem “choosing” elements in one case, the same problem must also exist in the other case, and if we do not have such a problem in the one case, then we also do not have the problem in the other.103 Rather, the main value for modern set theory of an “axiom of choice” seems, no different from the axiom of infinity in ZF, to be rooted in the uncertainty modern set theorists have about the nature of infinity, which uncertainty itself is based on, as we have discussed, the logical error of conflating the finite and the infinite. In the idiosyncrasies of set theory as it is currently designed, the union of a finite system of finite sets is easily understood without AC because we can conceive of a pattern, a finite algorithm, by which we may enumerate a finite collection of elements at each iteration of the pattern whereby the resulting collection at that iteration is equal in finite magnitude to the total number of sets being unioned and contains exactly one element from each of these sets. These elements can then easily be place in one-to-one correspondence with a finite collection of natural numbers and, thus, their entirety can be lined up in the union set. But we start running into problems as soon as the number of sets being unioned is countable. In this case, the same process does not quite seem to work, because something we once clearly perceived to be finite, viz., the pattern by which each round or iteration of elements was chosen across the sets being unioned, is no longer finite, i.e., it never finishes, because the list of sets being unioned now grows without bound; we are taking a process that once involved making a finite number of choices per iteration equal to the finite number of sets being unioned, and turning it into a process that, at each iteration, must now make an infinite number of choices. In other words, something that has given us a sense of control over the task of unioning the sets now has been taken away and replaced with something that cannot be circumscribed in its entirety and treated as a finite, repeatable thing or process. If we stick to this particular idiosyncratic way of unioning an infinite list of finite sets, then of course we will encounter difficulties and confusion in how to properly perform the process; and we may also feel the need to create a new axiom104 that says, effectively, that even though this pattern by which we select elements from the sets being unioned is never complete (and thus is not technically a pattern at all, because it is not a finite process or algorithm) even for a single iteration, it can somehow be “made complete,” so that we can complete the process of union that seems so obviously possible between the sets in this countable collection of finite sets. In other words, the axiom of choice, in this regard, is another example in set theory of the conflation of the finite with the infinite. Like the axiom of infinity in ZF, AC is made more useful than it otherwise would be by the fact that it gives us additional justification for conflating the finite with the infinite when we wish to do so in the process of unioning or enumerating or creating sets. If we do not need to conflate the finite with the infinite in such processes, the axiom of choice is not felt to be needed and is not invoked; this is borne out by the fact that Hrbacek do not invoke the axiom of choice to prove that every finite system of sets has a choice function, but only define the axiom of choice later on the same page specifically so that the choice function can be extended to infinite sets.105 But there is no reason why, in order to create the union of a countable collection of finite sets, we cannot line up the sets in arbitrary order (as was effectively done in the earlier discussion regarding a finite collection of either finite or countable sets) and enumerate the elements in the first set first, placing these elements in one-to-one correspondence with the first n natural numbers if the first set has n elements, and then repeat this process for the second set, then the third set, etc.; and, in fact, this is equivalent to the process that was laid out above for finite collections of countable sets, after, essentially, a mirror reflection. And yet the latter is accepted in modern set theory as valid without the axiom of choice, while the former is not. The assumption that there even is such a distinction is itself a symptom of the confusion in modern set theory regarding the nature of infinity.
But it may be objected that if we create the union set of a countable collection of finite sets by the procedure I have spelled out above which does not invoke the axiom of choice, this process will never end, and so the union of these sets can never be completed in this way. But this is exactly the point. The process I have spelled out above makes clear the infinite nature of such a union, i.e., that such a union can never be completed because its definition is a pattern that can be repeated as many times as we like, without end. The axiom of choice, on the other hand, obscures this fundamental reality of infinity, and, in fact, this is part of the value of the axiom of choice in modern set theory, and the axiom of infinity in ZF as well, viz., to allow us to feel more comfortable than we otherwise would in committing the logical error of conflating the finite with the infinite, so we may believe that we have been able thus to further finitize infinity.
The same argument also applies to the union of a countable collection of countable sets. The sets can be listed in arbitrary order, with the first elements of each set lined up on the left (and it makes no difference which order the elements in each set are in) so that in the partial representation of the list of these sets (which is all we could ever write down) we have a “square” or “rectangular” listing of elements across the sets; then, we can perform a sort of “diagonal” process that starts with the first element of the first set, goes to the second element of the first set then the first element of the second set, then goes to the third element of the first set, the second element of the second set, and the first element of the third set, etc., and in this way we can enumerate, i.e., put in one-to-one correspondence with the natural numbers, all the elements of the entire countable collection of countable sets, without in any way relying on or invoking the axiom of choice in order to finitize infinity. It simply must be remembered that though the pattern producing the union set is finite, the union set itself and the sets being unioned are infinite, and though it may be convenient or practically useful for various purposes to think of the two as being equal, they are, in fact, different types of mathematical object, and so in reality are not equal; if we clearly understand this, then we will understand that there is no way to actually finitize the infinite in creating such a union, and this, in turn, means that the axiom of choice is reduced in usefulness. We may also say that this “diagonal” process is the exact same process that could be used for a finite collection of countable sets, say two sets with one being the odds and the other the evens, and this operation too would not need the axiom of choice in order to finitize infinity in the process of choosing elements, since, as with countable unions, we do not actually need to finitize infinity in order to clearly define and understand the nature and construction of the union set.
Further, in the case of the so-called “uncountable” sets whose existence “requires” the axiom of choice, such as the uncountable, non-measurable set needed in the Banach-Tarski theorem to prove that a unit sphere can be deconstructed and reconstructed into two unit spheres, we recognize (a) that, as we have discussed, there is no actual difference between “countable” and “uncountable” infinity, because “countable” infinity never finishes, since it is infinite, and it does not make sense to invoke a new axiom to help explain or justify the existence of something that cannot logically exist, and (b) that any infinite collection of fixed, i.e., finite, entities or elements is countable because these elements can always be placed in one-to-one correspondence with the natural numbers.
The axiom of choice seems to “work” and to be “helpful” and “useful” in the case of countable collections or sets only because in applying or invoking the axiom of countable choice we make reference to infinite sequences of elements whose existence and nature can be, as with the example of the countable collection of two-element sets above, meaningfully understood, i.e., neither the resulting set or sequence itself nor any countable set used in its creation contains a logical contradiction in its definition. But the crucial thing to remember here is that the only reason these sets can be meaningfully understood is that they are sets which can be produced by explicit enumeration, i.e., one-to-one mapping with the natural numbers, of their elements – that is, an infinite set which can be meaningfully under-stood and contains no logical contradictions in its definition is precisely a set which can be enumerated by the natural numbers. There is no difference between these two “types” of set, i.e., they are identical. The fact that invoking the axiom of countable choice can allow for a set that we perceive to be logically valid in its structure and clearly understandable is not a virtue of the axiom of countable choice, but of the fact that we have a prior, logically valid intuitive understanding of the countable nature of such a set; further, this intuitive understanding guides our invocation of the axiom of countable choice, and essentially determines when we find it useful to invoke the axiom of countable choice in our investigations and proofs. If we properly understand infinity, we will realize that our intuitive understanding, i.e., our rational recognition of patterns, by itself is sufficient for the task of producing and understand-ing the nature of such sets, so long as we do not fall prey to subconscious biases and emotional impulses that warp and obscure our rational capacity (such as, for example, the strong desire to, in one form or another, finitize infinity); and that, therefore, from the perspective of grasping the true nature of infinity, viz., that it is countable only, and using this understanding fruitfully in set-theoretical and mathematical work, the axiom of countable choice, much less the full AC, is nothing more than a redundancy, entirely eliminable without loss, and with a resulting gain in clarity.
Hrbacek state, “The reader might be well advised to analyze the reasons why this proof [that every finite system of sets has a choice function] cannot be generalized to show that every countable system of sets has a choice function.”106 However, we have already discussed this: a misapprehension of the nature of infinity and the idiosyncrasies of set theory in proving the case for finite systems of sets make it so that an extension of these ideas to considerations of an infinite number of choices does not seem as plain or as clear as was the case with a finite systems of sets; and, further, this extension requires the finitizing of the infinite, because otherwise the extending of a finite pattern for selecting or choosing numbers from different sets in the case of countable collections of sets will never finish, and thus will contradict the inherent meaning of “pattern,” which always simply means a finite, repeatable process. It is not surprising that set theorists feel the need to invoke a new axiom to allow for the existence of sets made by making an infinite number of choices from an infinite list of sets, because it is precisely at this point that the standard way of viewing the operation of choosing elements from a list of sets to produce a completed choice set breaches its bounds of applicability and forces us to directly face the bare nature of infinity, so that, unlike single infinite sets such as that of the natural numbers or the rationals, for which we already have an axiom that has allowed us to desensitize ourselves to the logical error inherent in the finitizing of the infinite for these sets, we are faced with a key problem that, once again, we greatly desire to solve, but do not know how to solve in a strictly logically deductive manner. If, on the other hand, the “choice” process is done in the alternative way spelled out above, there is no need to create a new axiom in order to perform a unioning process for a countable list of sets, since the process of “choosing” elements in this countable list of sets is no different from the process of “choosing” elements from a finite list of sets; we must simply remember that because the list of sets is infinite, the unioning process can never complete – no different from unioning a finite list of countable sets – and that this reality about the nature of infinity is precisely what set theorists wish to sweep under the rug in their own minds by postulating a new axiom which says, by arbitrary decree, that this infinite unioning process somehow can complete. In other words, the reason why the result about finite systems of sets cannot be generalized to countable systems, as Hrbacek state, is that there is a key difference between a finite collection of elements, on the one hand, and an infinite collection of elements that we wish to finitize, on the other. Set theorists recognize this difference, and postulate a new axiom in part to cover this situation in the context of unions of countable systems of sets; however, the recognition in set theory of this difference is only surface-level, i.e., it does not go deep enough to permit us to see the true nature of infinity. The axiom of choice, in other words, allows us to gloss over, and effectively ignore, a process of finitizing the infinite, so that we may continue to believe that there is no logical error in doing this.
Further, Hrbacek state, “Also, while it is easy to find a choice function for P(ℕ) or P(ℚ) (why?), no such function for P(ℝ) suggests itself.”107 But in the context of the ideas and conclusions of this paper, we can understand why it is so hard to find a choice function for the power set of the reals. First, we say that it is easy to find a choice function for the power sets of the naturals and the rationals because we have a clear method of determining, for any natural and for any rational, a finite representation of these numbers, and so in creating their power sets it is clear that we are creating sets with finite numerical elements, i.e., there is no part of selecting the numerical elements for the power set of the naturals or of the rationals that involves the logical error of conflating the finite and the infinite, as long as we do not assume that any of the infinite sets involved in this process are or can be made into fixed or finished collections. But it is different with the reals, because for many of the reals, it is impossible to create a finite representation of their exact magnitude in numerical form. The operation of choosing an element of a set assumes that the elements are fixed, finite things, and so the entirety of each element can be chosen, can be moved or copied into another location, another set. But the reals whose decimal representations never repeat or terminate cannot be chosen in this sense if we choose to equate such a real with its non-terminating decimal expansion, because these decimal expansions are sequences of ever more minor adjustments in magnitude that never end, and so the thing itself that would be chosen never actually exists because it is never fixed, i.e., never finite, complete, or finished. But then, we know that the limit points of these decimal sequences are themselves finite, and therefore fixed, and so these limit points, or, e.g., fixed Euclidean magnitudes or distances, can be chosen the same way the naturals or rationals can be chosen, i.e., in their entirety. We can clearly see that real numbers are finite, and thus should be able to be chosen, but this conflicts with our understanding that many real numbers have non-repeating, non-terminating decimal sequences, whose significance in relation to real numbers is (erroneously) enhanced by their use as real numbers in the diagonal argument. This creates confusion and uncertainty, because we think that these numbers should be able to be chosen, and yet in some subtle way they are not the same as what we typically think of when we think of something that is able to be chosen. Also, we labor under the false impression that the reals are uncountable, and thus cannot be entirely enumerated, and so we remain foggy on just how elements are supposed to be selected from such a set, and on how we are to find a selection process that can ensure the creation of all possible subsets of such a set. If we do not at this point acknowledge the logical error in the conflation of the finite with the infinite, then in order to overcome the hurdle presented to us, we might feel tempted to postulate a new axiom that says by fiat that what we wish to be the case, and what seems, at a certain level, like it should logically be the case, actually is the case, and then, armed with this new axiom, we simply ignore the logical error which we have glossed over by creating the axiom and proceed for all practical purposes as if the axiom is or must be true, because, frankly, we have no idea how to resolve the logical error, or do not wish to have such an idea.
Hrbacek provide a theorem which says, “A set A can be well-ordered if and only if the set P(A) of all subsets of A has a choice function.”108 Then on the next page, in their lead-up to their statement of the axiom of choice, they first prove that every finite system of sets has a choice function and then discuss the implicit use of choice functions for infinite systems of sets of reals by mathematicians and the opacity involved in finding a choice function for the power set of the reals as motivations for the axiom of choice. They then state the axiom of choice, which says, “There exists a choice function for every system of sets.” But then let us take P(ℝ) as our system of sets. The axiom of choice then states that this system of sets has a choice function. But then the theorem just mentioned says that if this system of sets has a choice function, then the set ℝ is well-orderable. But if ℝ is well-orderable, then it must be countable. But a key reason for the use of the set ℝ as motivation to justify the axiom of choice is that ℝ is uncountable, which then is supposed to make it difficult to find a choice function for its power set. It would appear, then, that if we assume that P(ℝ) is a meaningful operation that produces a meaningful set, the axiom of choice is incompatible with the idea that ℝ is uncountable. On the other hand, if we assume that ℝ is uncountable, then P(ℝ) cannot be a meaningful operation that produces a meaningful set, which means that the axiom of choice cannot be used to allow for the production of infinite choice sets from the power set of the reals. We should also note that part of the motivation of creating the choice function in the first place, as explained by Hrbacek on pp. 137-38, is to find a way to order, or enumerate, sets that are not well-orderable, or at least not obviously well-orderable, i.e., that we cannot seem to find a way to map one-to-one with the natural numbers. In these cases, we define a choice function that allows us to choose elements from a (presumably) non-well-orderable set one by one, i.e., that allows us to effectively make the non-well-orderable set well-orderable. Notice though that this does not prove that non-well-orderable sets are well-orderable, but simply states that if a choice function can be shown to exist for the power set of such a set, then the set must be well-orderable, and vice versa. But the reals themselves, and, in fact, all uncountable sets, are precisely this kind of set, i.e., sets that are not well-orderable. It would thus appear that a primary motivation for the axiom of choice is to make uncountable sets well-orderable, and thus countable. This is another example of the confusing and contradictory results that can be obtained when a logical error is embedded and interweaved into a system of ideas; and the more time we have to interweave it, the more its paradoxical and contradictory implications can be altered or reworked so that they no longer appear to us as contradictions and paradoxes.
We should note also that the distinction that Hrbacek make between the power sets of the naturals and the rationals, on the one hand, and the reals, on the other, ignores the fact that many of the rationals also have non-terminating decimal sequences. It is assumed that because the rationals can all be written as ratios of integers, and thus have what we can clearly perceive to be a particular finite representation, none of the rationals must fall prey to the lack of clarity issue when determining a “choice function” for the rationals. But this also is to conflate the finite with the infinite, and thus to ignore the essential sameness, with regard to the difficulty of determining a choice function, between the irrationals, all of which are non-terminating, and the non-terminating rationals. A sound understanding of infinity would make this plain, because it would allow us to clearly see the true meaning, significance, and perceived usefulness of the axiom of choice in set theory.
Hrbacek state that “… in 1963, Paul Cohen showed that the Axiom of Choice cannot be proved from the axioms of Zermelo-Fraenkel set theory … . The Axiom of Choice is thus a new principle of set formation; it differs from the other set forming principles in that it is not effective. That is, the Axiom of Choice asserts that certain sets (the choice functions) exist without describing those sets as collections of objects having a particular property. Because of this, and because of some of its counterintuitive consequences … some mathematicians raised objections to its use.”109 But of course. ZF without choice is about finite sets of finite elements, with the exception of the axiom of infinity, which states that an inductive set exists. An inductive set is infinite, because it maps one-to-one with the natural numbers. But the axiom of choice is, in a sense, about infinite sets that do not have a property on all their elements that can be proved inductively, so in this sense we cannot justly say that the axiom of choice is about inductive sets; and this gives us an understanding of the reasoning behind the word “choice” in the name of the axiom, since choices, as we typically think of them, are made by humans with free will, and thus there does not necessarily have to be a rhyme, reason, or pattern to them. We can imagine, then, that the creation of such sets is not explicitly allowed for by the axioms of ZF by itself; thus, if we wish to ensure that all types of set which we consider or encounter in our set theory are explicitly allowed for by one or more of our set theory’s axioms, then for sets whose elements are based on “choice” to exist in our set theory we may feel the need to add an axiom to ZF that explicitly allows for them. Thus, since under this understanding the sets created by AC cannot be created by the ZF axioms, Hrbacek are correct that AC is a “new principal of set formation.” Of course, they also say that AC differs from the other principles of set formation in that it is “not effective,” i.e., it states that certain sets exist without specifying the particular properties of the elements that make up the sets, or even the elements themselves or how they get into the sets, except that they are “chosen” somehow from other sets in order to be members of the sets in question. Now, the concept of the “choice” of an unknown number of elements from one or more sets in order to create a new set is not a logically contradictory concept. The problem with AC is not the “choice” aspect itself, but the fact that AC is typically brought in, and typically useful in, the context of the conflation of the finite with the infinite, whether countable or uncountable. In the absence of the need to do this, AC serves only a technical purpose. Without further investigation, we cannot say which particular objections to AC were raised by which of the mathematicians to whom Hrbacek refer, or for what reasons. But we may reasonably say that at least some of them, in raising their objections, perceived that there was something not quite logically sound about the axiom of choice, though perhaps they were not able to put their finger on it. The typical use of the axiom of choice is based on the same logical error as any of the large cardinal axioms, and as the axiom of infinity in ZF, because all of these assume that it is logically valid to equate the finite with the infinite, when, in fact, this is not the case.
In their introduction to uncountable sets in Chapter 4, early on in their book, Hrbacek state, “All infinite sets whose cardinalities we have determined up to this point turned out to be countable. Naturally, a question arises whether perhaps all infinite sets are countable. If it were so, this book might end with the preceding section.”110 Indeed. They go on to state, “It was a great discovery of George Cantor that uncountable sets, in fact, exist. This discovery provided an impetus for the development of set theory and became a source of its depth and richness.”111 They then go on to discuss the uncountable nature of ℝ, and Cantor’s famous diagonal argument. But we have already shown in the previous part that the diagonal argument is flawed, because it conflates the finite with the infinite. Furthermore, we have shown that this same flaw is at the root of the persistent opaqueness and intractability of CH and generalized CH, which Cantor himself proposed on the basis of his flawed theory of the infinite, and which he was unable to resolve; and we have shown how to resolve CH and its generalization by recognizing and removing the logical flaw from our understanding of sets. But without the conceptual scaffolding which we use to prop up, and hide to ourselves, our denial that there is a logical error in conflating the finite with the infinite, a substantial portion of modern set theory, really the bulk of it, is itself shown to be flawed, and thus not representative of reality. It may still be an interesting mathematical exercise to try to investigate the “structure” of the cardinals and ordinals, on the assumption that there are no logical contradictions in such a theory, or at the foundation of such a theory. Nonetheless, if it is clearly perceived that such investigations are based on a logical error, then interest in them cannot really be held to as high a level as it was when, in the “golden era” of set theory, we had succeeded in convincing ourselves that our investigations were entirely logically sound. Unmask the illusion, and it becomes much harder to justify expending the effort to preserve it.
After providing detailed proofs of various important mathematical results that depend on the axiom of choice, Hrbacek state that “there are many fundamental and intuitively very acceptable results concerning countable sets and topological and measure-theoretic properties of the real line, whose proofs depend on the Axiom of Choice… . It is hard to imagine how one could study even advanced calculus without being able to prove them, yet it is known that they cannot be proved in Zermelo-Fraenkel set theory. This surely constitutes some justification for the Axiom of Choice. However, closer investigation of [two of the proofs given that involve AC] reveals that only a very limited form of the Axiom is needed; indeed, all of the results can still be proved if one assumes only the Axiom of Countable Choice,” which states, “There exists a choice function for every countable system of sets.”112 This we may contrast with the full axiom of choice, which extends the choice function capability to uncountable sets. They then go on to say, “It might well be that the Axiom of Countable Choice is intuitively justified, but the full Axiom of Choice is not. Such a feeling might be strengthened by realizing that the full Axiom of Choice has some counterintuitive consequences, such as the existence of nonlinear additive functions … or the existence of Lebesgue nonmeasurable sets … . Incidentally, none of these consequences follows from the Axiom of Countable Choice.”113 Here we may make a number of observations. Notice that the “intuitively” very appealing results which they mention concern countable sets, i.e., sets that are infinite but whose particular infinite nature we can clearly understand, i.e., sets which are representative of nothing more or less than precisely what infinity is, viz., the quality of increasing without bound, and it is easy to understand the nature of this increase. This is why such results are both intuitive and appealing. The fact that these infinite sets may not be able to be produced inductively, in the sense described above, and thus may not be able to be produced on the basis simply of the axiom of infinity in ZF, does not make them any more difficult to understand, since the pattern of the successor function that creates elements of an inductive set has simply been replaced with the pattern of choosing an element, and since this, like the successor function, can be repeated as many times as we like, we may conclude that in both cases it is possible to produce a sequence of fixed elements whose quantity can grow without bound, i.e., an infinite sequence. This is easily understandable because the axiom of choice when used to produce countable sets produces sets, or sequences, that are accurate representations of infinity, even though in treating the resulting infinite sequences as “sets” in the sense of completed collections, we are still making the logical mistake of conflating the finite with the infinite – though, as with the “set” of naturals or the “set” of rationals, and even the “set” of reals when the reals are treated not as their infinite decimal expansions but as their finite, fixed magnitudes or limit points, it often does no harm to equate the finite pattern that produces the elements with the infinite sequence of elements itself, as a practical convenience. It is, thus, not surprising that we are told that when we restrict AC to countable collections, the results are intuitively appealing or acceptable and intuitively correct – i.e., the results are not counterintuitive. Results in advanced calculus that use AC in their proofs, for example, are intuitively appealing and intuitively correct because these results are restricted to the creation and use of countable collections of elements. This does, as Hrbacek state, “[constitute] some justification for the Axiom of Choice,” but Hrbacek do not see the full reason why they feel this sense of justification. What they see is that AC, when restricted to countable collections, just seems to work in various areas of mathematics, but they do not understand why it works.
Hrbacek then go on to state, “In our opinion it is applications such as [the Hahn-Banach Theorem] which mostly account for the universal acceptance of the Axiom of Choice. The Hahn-Banach Theorem, Tichonov’s Theorem ..., and Maximal Ideal Theorem … are just a few examples of theorems of sweeping generality whose proofs require the Axiom of Choice in almost full strength; some of them are even equivalent to it. Even though it is true that we do not need such general results for applications to objects of more immediate mathematical concern, such as real and complex numbers and functions, the irreplaceable role of the Axiom of Choice is to simplify general topological and algebraic considerations which otherwise would be bogged down in irrelevant set-theoretic detail. For this pragmatic reason, we expect that the Axiom of Choice will always keep its place in set theory.”114 Any mathematical result that requires the existence of uncountable sets is itself based on the same logical error that assumes there is a difference between countable and uncountable infinity, i.e., that there are different “levels” of infinity. Such results may be valid in the context of assumptions and definitions that already assume that there are different levels of infinity, but they are not valid in a universal, contextless, logically necessary sense, nor, because of this, in an intuitively acceptable sense. Without digging into the details of these theorems that Hrbacek list which require AC at almost full strength or which are equivalent to it, we may still say that this is likely the reason such results are not relevant for “objects of more immediate mathematical concern,” since the latter type of object remains within the realm of intuitive sense, and thus countable infinity. And of course, if a particular branch of mathematics is deemed to be based on the set-theoretic principles of ZF, then any countable collection of elements we wish to use in this branch of mathematics but that we cannot see how to produce inductively would, if we are to be explicit about every set that can be produced in set theory, and thus in this particular branch of mathematics, require that we tack on another axiom saying that it is possible for countable sets to be produced non-inductively, i.e., to be produced not according to any identifiable pattern. But the reason that it still makes sense to say that such sets can exist and are non-contradictory is that the method of producing them actually does use a pattern, the pattern of choosing an element, which is repeated over and over as many times as we like. This pattern is not the “successor function” of mathematical induction, but it is a pattern nonetheless and is represented in set theory by the “choice function.” By understanding the key difference between the pattern that produces an infinite sequence, and the infinite sequence itself, we can come to understand that there is an essential similarity between the infinite sequence of natural numbers produced by the successor function and the infinite sequence of numbers produced by the “countable choice” function, in that both are infinite sequences that accurately express the nature of infinity and which are produced by a finite algorithm, a pattern. This is the essential reason why both types of set make intuitive sense and can be used to produce intuitively acceptable, and logically valid, results. Given the strict nature of the definitions of the axioms of ZF, we may feel it useful in a technical sense to add another axiomatic statement to ZF that explicitly says that it is possible to produce “non-inductive” countable sets. But the point is that if we have a clear understanding of the nature of infinity, we can demystify the axiom of choice and see that, in its countable variation, it is not any less understandable or logically comprehensible than the axiom of extensionality, the axiom of pair, the axiom of union, etc., or the axiom of infinity; and, further, we can understand why it is necessary to completely discard the uncountable component of the full AC if AC, and ZFC by extension, are to represent reality, or a part of reality, accurately. From the perspective of creating an infinite countable set, the axiom of infinity and the axiom of choice stand on equal grounds of comprehensibility, and have, in essentials, the same underlying structure – in fact, any set produced by the countable choice process by any sort of algorithm that can be repeated over and over as many times as we like as we are choosing element across the sets (which effectively means any set produced by the countable choice process), i.e., by any pattern, can be produced inductively, by mapping the natural numbers one-to-one with iterations of the pattern, proving that the first iteration produces a finite set of elements that conform to the pattern, and then proving that if the nth iteration produces a finite set of elements that conform to the pattern then so does the (n+1)th iteration. This is an illustration of the deeper underlying sameness between the two countable infinity axioms, and of the fact that the nature of infinity itself is unitary, not split into different “kinds” or “types,” so that any accurate expression of infinity will be fundamentally the same as any other (superficially different) accurate expression of it. Even when elements are chosen from sets at random, this is still a pattern that can be represented inductively, just in an unorthodox way; it is the pattern of choosing an element in its most bare-bones form, but it is a pattern, i.e., a finite algorithmic process that can be repeated as many times as we like, nonetheless, and as such it can be mapped one-to-one onto the pattern of the natural numbers themselves. What really distinguishes the axiom of infinity in ZF from the axiom of countable choice is the relative clarity we feel we have with regard to how to specify elements in the former case and the relative lack of clarity we feel we have with regard to how to specify elements in the latter case, which lack of clarity is due to the fact that “choice” is associated with free will, and thus “lack of pattern,” which, in turn, brings in a certain level of indeterminateness and which we seek to capture formally by the so-called “choice function.” But all the choice function represents is the repetitive process, i.e., the pattern, of choosing an element, and as such there is no fundamental difference between the choice pattern on the one hand and the pattern of the successor function on the other. Finally, we should note that in the sense that AC helps us conflate the finite with the infinite, AC is at best a useful convenience, no different from the axiom of infinity in ZF, and we must remember that all such conveniences have bounds of applicability, beyond which they produce nonsensical results.
Hrbacek say that the important role in simplifying mathematical proofs in other branches of mathematics is the “pragmatic reason” why they believe that the axiom of choice will remain a cornerstone of set theory. This makes sense, because if we simply assume, via a new axiom, that non-inductive countable sets can exist as completed totalities, then we do not need to spend a potentially great amount of effort trying to prove the existence of such a set by other, more primitive methods. But there is also another reason the use of AC is “pragmatic,” and it is the same reason the use of the axiom of infinity is pragmatic, viz., that it contains within it a practically useful conflation of the finite and the infinite. If we assume that such infinite, completed sets can exist, it makes it easier to proceed with our mathematical investigations than if we were to constantly keep in mind the reality that such sets can never exist as completed things. In this way, AC and the axiom of infinity are practical tools or conveniences to make mathematical work easier.
Hrbacek state that it may be that the full AC is not justified, but that the axiom of countable choice is. This shows a certain level of deeper understanding. But we do not fully comprehend things until we understand why we feel that this distinction should be made in the first place, and why it has been made in broader mathematics. The reason, as we have discussed, is that there is no such thing as different “levels” of infinity, and so countable and uncountable do not represent different “levels” or “types” of infinity. It is because of this that the full AC, which extends the choice function capability to uncountable sets, (a) produces nonsensical mathematical results and (b) is difficult to understand intuitively, i.e., we find it difficult to understand how the uncountable component of AC can be true or justified. As with CH, it is impossible to understand something that is based on a logical error, since the logical error will inevitably show itself as permanent opaqueness and intractability in certain parts of our theoretical framework. Once we appreciate the logical error at the foundation of modern set theory’s understanding of the infinite, we can see clearly why the axiom of countable choice seems justified but why full AC’s status is not so easily determined.
Hrbacek state, “An infinite cardinal 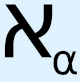 is a strong limit cardinal if
is a strong limit cardinal if 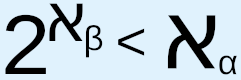 for all β < α … . An uncountable cardinal κ is strongly inaccessible if it is regular and a strong limit cardinal… . The reason why such cardinal numbers are called inaccessible is that they cannot be obtained by the usual set-theoretic operations from smaller cardinals … .”115 But do such statements correspond to anything in reality, i.e., are such statements representative of any aspect of contextless logical necessity? As with CH and generalized CH, we are relating supposedly differing infinite quantities by treating them as if they were finite. The only thing that makes such relations even seem to make logical sense is that we are already so familiar with treating and relating finite quantities by use of variable letters that it is no great leap to do this for infinite “quantities” as well, once we assume that it is possible to finitize infinity. But in treating of these transfinite “numbers,” we must understand that by drawing various “conclusions” and proving various “theorems” and “corollaries” and “lemmas,” etc., and by creating definitions that give names to certain things based on certain relations between transfinite “numbers,” we have come no closer to understanding infinity, or the “structure of infinity,” than without such ideas, conclusions, and definitions. In fact, the only reason such investigations are interesting to us is that we continue to labor under the false impression that by investigating such things, by defining and concluding such things, we are, somehow, making measurable progress in understanding infinity. If we come to no longer believe that measurable progress can be made in this way, then such investigations will no longer be interesting to us.
for all β < α … . An uncountable cardinal κ is strongly inaccessible if it is regular and a strong limit cardinal… . The reason why such cardinal numbers are called inaccessible is that they cannot be obtained by the usual set-theoretic operations from smaller cardinals … .”115 But do such statements correspond to anything in reality, i.e., are such statements representative of any aspect of contextless logical necessity? As with CH and generalized CH, we are relating supposedly differing infinite quantities by treating them as if they were finite. The only thing that makes such relations even seem to make logical sense is that we are already so familiar with treating and relating finite quantities by use of variable letters that it is no great leap to do this for infinite “quantities” as well, once we assume that it is possible to finitize infinity. But in treating of these transfinite “numbers,” we must understand that by drawing various “conclusions” and proving various “theorems” and “corollaries” and “lemmas,” etc., and by creating definitions that give names to certain things based on certain relations between transfinite “numbers,” we have come no closer to understanding infinity, or the “structure of infinity,” than without such ideas, conclusions, and definitions. In fact, the only reason such investigations are interesting to us is that we continue to labor under the false impression that by investigating such things, by defining and concluding such things, we are, somehow, making measurable progress in understanding infinity. If we come to no longer believe that measurable progress can be made in this way, then such investigations will no longer be interesting to us.
We are told in Hrbacek, “Every system of mutually disjoint open intervals in ℝ is at most countable.”116 This makes sense, given that each interval is a fixed, unchanging entity, though it represents an infinite “collection” of numbers, and given that there is no overlapping of intervals. There is, therefore, a clear way to map these intervals one-to-one with the natural numbers, and since the sequence of natural numbers never ends, the sequence of these intervals, with each representing a single entity, never increases in magnitude beyond that of the natural numbers. We must be careful here, because each interval is a “collection” of an infinite number of numbers, and because each interval is open and so does not technically have endpoints, but rather only ever approaches the two fixed points at either end. However, these problems can be made insignificant by taking a single rational number in each open interval and identifying it with the fixed, geometric line segment that represents the interval in which the chosen rational resides, and then mapping these single rational numbers to the naturals, which, in turn, is a one-to-one mapping of the intervals to the naturals. This works because the rationals are dense in the reals, and so no matter how small the disjoint intervals are, there will always be at least one rational (and, in fact, an infinite number of rationals) in each interval. Also, even for rationals whose decimal expansions do not terminate, we already know that such rationals have a finite representation that we can take advantage of in the proof, should we choose to use them in the proof, that equates each such rational with a ratio of integers, in addition to the rational being a fixed point in its interval, so we do not need to restrict the proof to using rationals whose decimal expansions terminate. This is how the proof of the statement proceeds in Hrbacek. But the proof is equally valid if we choose a particular irrational number in each of these intervals, so long as we represent these irrationals by their limit points and not by their non-terminating decimal sequences.
Hrbacek then introduce “a famous problem in set theory dating from the beginning of the [20th] century: Let (P, <) be a complete linearly ordered set without endpoints where every system of mutually disjoint open intervals is at most countable[, but which has no countable dense subset]. Is (P, <) isomorphic to the real line? This is the Suslin’s Problem. Like the Continuum Hypothesis, it remained unsolved for decades. With the help of models of set theory, it has been established that it, like the Continuum Hypothesis, can be neither proved nor refuted from the axioms of Zermelo-Fraenkel set theory.”117 Suslin’s question, then, is whether there is a line that is equivalent to the real line, or, more correctly, isomorphic to it, but that does not have, as the real line has with, e.g., the rationals, a countable dense subset. Such lines, if they exist, are called Suslin lines. With the addition to ZFC of certain axioms based on transfinite numbers, one can either prove that Suslin lines exist, or that they do not, depending on which axiom is added (e.g., if Jensen’s Principle ◊ is assumed, Suslin lines exist, but if Martin’s axiom 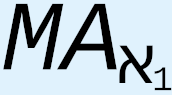 is assumed, they do not).118 A linearly ordered set is complete if it has no gaps, i.e., if there is no “point” or “spot” of discontinuity in the linear ordering such that the segment below this spot contains no supremum and the segment above the spot contains no infimum. The canonical example of the completion of a non-complete set is the use of the irrationals, which reside in the “gaps” between the rationals in the real line, to complete the rationals and thus make the reals. The rationals are dense, but they have gaps because between any two rationals, no matter how close, there can always be located at least one irrational.
is assumed, they do not).118 A linearly ordered set is complete if it has no gaps, i.e., if there is no “point” or “spot” of discontinuity in the linear ordering such that the segment below this spot contains no supremum and the segment above the spot contains no infimum. The canonical example of the completion of a non-complete set is the use of the irrationals, which reside in the “gaps” between the rationals in the real line, to complete the rationals and thus make the reals. The rationals are dense, but they have gaps because between any two rationals, no matter how close, there can always be located at least one irrational.
But remember that in standard set theory it is understood that the rationals are countable, i.e., they can be placed in one-to-one correspondence with the natural numbers. It is easy to see this because the definition of the rationals contains a specification that forces all rationals to have a finite representation, viz., a ratio of integers, and so it is not difficult to see how each of these can be made to correspond to a single natural number in an index sequence. But the irrationals are different because, as we have discussed, there seems to be no way to represent an irrational number as a finite numerical entity without abstracting away too much (e.g., in saying that π = C/d) or running afoul of a clear, and thus obvious, violation of the logical error of conflating the finite with the infinite (e.g., we know and can see clearly that 3.14159 ≠ π). There is not even a general rule of some kind by which all irrationals can be represented as formulas that are heavily abstracted, such as π = C/d, while, on the other hand, the rationals all conform to the single formula that says that to be a rational means to be a ratio of integers. But the reason why there is always at least one irrational (actually, infinitely many) between two rationals, as well as at least one rational (actually, infinitely many) between two rationals, is that there can always be more numbers added at the end of any given finite decimal sequence, i.e., the task of adding a digit to the end of a decimal sequence is a pattern, i.e., a finite algorithm, and can thus be repeated as many times as we like. But remember that any decimal sequence that does not terminate is, in fact, not a number, because a number is a fixed, finite magnitude, whereas a non-terminating decimal sequence is an always-changing magnitude. What the non-terminating decimal sequence is is an approximate representation of a fixed magnitude, not the fixed magnitude itself. The fixed magnitude is, in the language of modern mathematics, the limit point of the ever-expanding decimal sequence, which the decimal sequence, since it is infinite, never reaches. And the reason why we think of these non-terminating, non-repeating decimal sequences as being “between” two rationals is that their fixed limit points represent Euclidean distance magnitudes between the fixed points of the Euclidean distance magnitudes of the two rationals, even if we would never be able, beyond a certain point, to actually measure such magnitude differences with scientific instruments due to how small the differences can get between any two rationals. In other words, it makes sense to say that there is at least one irrational between any two rationals because we can always take the “average” of the two rationals and then imagine a non-terminating, non-repeating decimal sequence beyond this point in the decimal expansion, and this is a clearly understandable, intuitive, logically valid process. (Non-terminating rationals can be cut off at a particular point before the average is calculated, and this point can be as far out into the decimal expansion as we like, so it can be as far out as we need in order to, say, match a particular level of accuracy we wish to match, or to match the length of the terminating decimal expansion of the other rational in the pair if the other rational is terminating.) Another way of saying this is that there is a clearly defined pattern, i.e., a finite algorithm, that we can see will produce as many digits as we like in any decimal expansion, and so such a process can never have a complete or full end, even though we may stop the process at a particular point for certain practical reasons. The same argument applies to the fact that any two irrationals have at least one rational between them, and that any two irrationals have at least one irrational between them.
But if the rationals are dense, how is it possible that their linear order has gaps? We may magnify the rational linear order as many times as we like, and there will always be infinitely many rationals that can fit in the magnified view, as well as in any subsequent magnified view. The reason this is possible is that decimal expansion representations of numbers are infinite, and this corresponds well with our intuitive notion that Euclidean space is continuous, i.e., that Euclidean space itself has no gaps; and, therefore, the limit points of these infinite decimal sequences have no length or dimension of their own and in fact are nothing more than positions on a line, if we choose to line them up. As discussed earlier, the problems start to arise when we make the logical mistake that any collection of such positions of zero length can create a non-zero, positive Euclidean magnitude.
But since it is the limit points of these decimal sequences, and not the decimal sequences themselves, that are the actual numbers on the real line, and since each limit point is a fixed, finite magnitude, every limit point can be made to correspond with a natural number, and thus the real numbers, which are these limit points plus all numbers that can be represented as terminating decimal sequences, are countable. This is the beginning of the process of unraveling Suslin’s Problem. Suslin’s Problem is based on the assumption that the reals are uncountable, and that the rationals within the reals are countable. Suslin then asks the question whether it is possible to have an uncountable set, specifically a set isomorphic to the reals, in which any collection of disjoint non-empty subsets is at most countable but in which there is no countable dense subset. Well, it is clear that it would not make sense to say that a collection of disjoint non-empty subsets would be anything other than at most countable, because it is too obvious how the subsets in any such collection can be mapped one-to-one with the natural numbers, or a finite subset of them; so this must be a property of Suslin lines if these lines are to have any, even indirect, meaning, i.e., if they are to be lines at all. The only thing left to consider, then, is whether it is possible to have a complete linear order (i.e., a “number line”) that is uncountable but that does not contain a countable dense subset.
But the answer must be no, because there is no such thing as an uncountable collection of numbers. It makes no sense to say that the infinite set of the rationals is dense “within” a larger, surrounding set of numbers that is “greater” in totality than the rationals themselves. The irrational numbers, being fixed points themselves, are both countable and dense within the reals, and so are the rationals, and thus the combination of the rationals and irrationals, which makes up the totality of the reals, is countable. Another way of looking at Suslin’s Problem, then, is to say that because a Suslin line can contain no countable dense subset, then it must not contain a subset isomorphic to the rationals; but in standard set theory the irrationals are uncountable, so in standard set theory Suslin lines could contain a subset isomorphic to the irrationals, and, in fact, in order to be isomorphic to the real line but not contain any subset isomorphic to the rationals, a set isomorphic to the irrationals or an uncountable subset of them must be part of Suslin lines. But then, as we have seen, the irrationals themselves in their entirety are countable, as well as dense, and so even if a Suslin line is isomorphic to the entirety of the irrationals, much less a subset of them, the Suslin line will still be at most countable, which is a contradiction of the definition of Suslin lines.
For the concept “dense” to be a fully clarified idea, we must ensure that it does not make any reference, even implicitly, to uncountable infinity; in particular, a set of numbers cannot be dense in an uncountable set. Also, the concept of a “gap” must be clarified, because currently it is assumed that the irrationals “fill in the gaps” between the rationals in the linear order. But actually, when represented as positions on a number line there will always be gaps, between any two rationals, any two irrationals, and between a rational and an irrational, no matter how close. Since decimal expansions of numbers can go out forever, providing ever-more accurate approximations of the limiting point numbers to which they approach, without ever actually reaching the limiting point numbers, and because there is an infinite number of real numbers, the process of “filling in the gaps” will never complete. The assumption that it does or that it can complete is an example of the conflation of the finite and the infinite, using an approximation between a linear sequence of a very large number of zero-length positions that are stretched out over an interval of a particular Euclidean length, e.g., 1 inch, and which interval is discontinuous everywhere, and the distance measure or magnitude of this Euclidean length itself, which is finite and continuous. Because points or numbers on the real number line do not have any dimension themselves, it is impossible for any number of them to ever create more than zero length together. If any two of the points are separated by a distance, no matter how small, it will be impossible to fill in the gap with additional points so that the linear order can become “complete” or “continuous.” We may define “gap” to be “those empty parts of the linear order in between the specified numbers of a partial set of real numbers that can be completely filled in by adding all the missing numbers of the sequence,” such as the “filling of the gaps” between the rationals by adding the irrationals, but then this this would just be another example of tailoring a definition so that what we want to say can be done, in this case the “filling in of the gaps,” we can actually say, per the definition, can be and has been done. In fact, even this definition is logically flawed, because the process of “filling in the gaps” in any sense can never complete, because such an act requires the adding of an infinite number of points to an existing set. Also, the concept of a “gap” seems inextricably tied up with the closing of gaps in a geometric line, and, as discussed, there is no way to arrange a linear order of real numbers, which always remains discontinuous at every point, so that the “gaps” between them are filled in a way that produces a geometric line, which is continuous. The conflation of the two, as with any conflation of the finite and the infinite, is an expression of the dissatisfaction the human psyche has with being “so close yet so far”: we seem to have defined the reals to be extremely close in nature to an actual geometric line, and yet no matter how hard we try, we are still somehow never able to get them to overlap identically, like a square block and a round hole, or two puzzle pieces that don’t quite fit. But after so much effort to get these two things to be equal, and in light of what it would mean mathematically if the two were equal, it is anathema to draw the conclusion that, fundamentally, they are as far from each other as night and day, and that the one is at most only a useful approximation of the other. So, our minds are emotionally incentivized to do the opposite, viz., to learn to think of the two as being identical, which then allows us to feel that our effort to equate them was not wasted, that, in other words, we did, in fact, achieve what we set out to achieve; and that we now have at our disposal a powerful, logically valid tool that connects geometry and analysis at a deep level, which we may make use of at our leisure. The human psyche desires to gain, not to lose. We desire power, not impotence. When nontrivial power seems to be nearly within our grasp, especially after we have fought so hard and so long to find it, our psyches are built to disincentivize the questioning of its existence or nature, for fear of missing a crucial opportunity to gain for ourselves; instead, we are psychologically and emotionally incentivized to accept the offer we are being given, and to obtain thereby a measure of certainty and security.
Another way of thinking about the reals is that they are countable and dense within empty space.119 As has already been said, this is not relevant for much of mathematics, which is satisfied with an approximation that glosses over the conflation of the finite and the infinite in this arena, since for such mathematical investigations it is not necessary to think about the essential difference between them too closely. But for certain questions, like Suslin’s Problem or CH, such a distinction becomes highly relevant. The reason we say that the irrationals fill the gaps between the rationals is that we make a subtle conflation of the finite with the infinite in thinking that since the decimal expansions can go on forever, we can get ever closer to any and all points on the linear sequence, and then when we think below or beyond a certain level of magnification or aggregation or number of digits in the decimal expansion, our minds automatically make the connection to and transition into the concepts of Euclidean length and distance. If we leave it at this, though, we have missed the points that (a) non-terminating decimal expansions never finish, and such representations of numbers will therefore never actually be numbers, and (b) since all numbers, rational and irrational, if we choose to place them in a linear order by magnitude, i.e., on a number “line,” are zero-length fixed positions on this line, then no matter how close we place them to each other, and how many we choose to aggregate, there will always be gaps so long as we do not put one in exactly the same position as another, in which case the positions no longer represent different numbers. We can ignore this for many considerations. But for certain problems, if we ignore this then we negate our ability to solve the problems.
Hrbacek are correct in pointing out the similarity between Suslin’s Problem and CH. In both cases, the problem to be solved is based on the logical error of conflating the finite with the infinite. Thus, in both cases, the problem is meaningless as stated and so cannot be solved, i.e., cannot be assigned a truth value. It is no coincidence that Suslin’s Problem is consistent with and independent of the axioms of ZFC, just as CH is. ZFC, at least if we restrict AC to countable choice, only references countable infinity, and thus accurately portrays the nature of infinity, albeit with the minor flaw that the axiom of infinity and the axiom of choice effectively state that completed infinite collections exist, and thus run afoul of the logical error that equates the finite with the infinite. But a statement that references different “levels” of infinity, such as Suslin’s Problem or CH, will be beyond the ability of the axioms of ZFC (with only countable choice) to comprehend. Such axioms will not be able to prove whether such a statement is true. Furthermore, any statement or question that itself is based on a logical error, such as a logically flawed understanding of infinity, will not be logically comprehensible in general, and thus will not be able to fit logically into an axiomatic system that does not already assume as true the logical error on which the statement or question is based. We can come to see this clearly after a proper clarification of concepts.
In discussing the axiom of countable choice, Potter makes the statement that “in the absence of the axiom … there is even a model in which the continuum is a countable union of countable sets… . It follows from this, moreover, that we cannot hope to eliminate the appeal to the axiom of countable choice from the proof we gave earlier that a countable union of null sets is null, since otherwise the model just mentioned would be one in which the whole real line is null, which is absurd.”120 But is it absurd? It is only absurd if we assume that an infinite collection of zero-length points can build up a line of positive, indeed infinite, length, i.e., if we already believe that it is possible to equate nothing with something. But after we have corrected this misconception, we find that this is exactly what the real line is, i.e., the real line is null. That is, if we try to line up the points on the real line so that there are no gaps between them, we may line up as many as we like and we will always end up with a line of zero length, i.e., the same nothing with which we started. On the other hand, if we marked off positions with these points that matched Euclidean distance magnitudes according to some distance scale, then no matter how many of these zero-length points we accumulated in this linear sequence, there will always be gaps, and, in fact, there will be nothing but gaps, since the point positions themselves do not add any length of line at all. The entire line so built would not exist to any degree, no matter how many points were accumulated. Once again, the idea that an actual continuous line such as that drawn by a pencil against a ruler could be built up out of an infinite linear collection of zero-length points is a practical conceptual tool that represents a useful approximation to the truth when used in the appropriate mathematical contexts; it is not a logically valid truth itself. Potter is correct in saying that a countable union of null sets (where a null set is a set of real numbers that “can be covered by a sequence of intervals of arbitrarily small total length…”121) is null, because, after all, no matter how many of these points are collected together, since they are each zero length they will never amount in total to any length greater than zero – and the implication in this definition is that we are talking about points; if we were talking about actual intervals of the line, no matter how small, then we could not say that the sequence of “intervals” we are considering has “arbitrarily small” total length. But the point is that there is nothing beyond this in terms of being able to accumulate “even more” points in some way which will allow the accumulation process to increase the length of the line beyond zero. To believe this is possible is to fall prey to the desire to finitize the infinite by “wrapping,” so to speak, an infinite, and indeed an “uncountably” infinite, number of points inside a finite Euclidean length; and also to the desire to find a way to analytically specify the geometric entity known as a line, based on the idea that analytical methods are, or at any rate can be, a more desirable format in which to do mathematics than geometric shapes, planes, and spaces. In marking off a fixed interval on a geometric line that we imagine accurately represents a linear sequence of the real numbers, we see clearly that this interval has a fixed, positive Euclidean length, and we know that any at most countable linear collection of points sums to zero length. Therefore, we conclude that the interval represents an uncountable collection of points, for what else could force a collection of zero-length points to sum to a non-zero, positive length? But it is this that is absurd. The flaw is in assuming that a continuous geometric line could ever be a fully accurate representation of a complete linear sequence of the real numbers, i.e., that the two are logically equal. Correct the flaw, and we remove the absurdity.
In a discussion about higher axioms of infinity, Potter states, “Higher axioms of infinity are responsible for many of the perplexities that the iterative conception throws up, since it seems to force on us not merely one such axiom but an endlessly growing hierarchy of them. We want to know how many levels there are in the hierarchy, but any answer we give can immediately be seen to be defective, since there could be … further levels beyond that. Each case we meet is an instance of the by now familiar phenomenon of indefinite extensibility writ very large. What these axioms exhibit, then, is that there is a sort of incompleteness implicit in the iterative conception itself. However, we have already encountered examples of incompleteness that do not seem to be of quite this sort.”122 He then discusses Suslin’s (“Souslin’s” in Potter’s spelling) hypothesis regarding Suslin lines and how it is undecidable in ZFC as modeled in first-order predicate logic, but that it is decidable in second-order logic. He then contrasts this with the incompleteness of the infinite sequence of bigger and bigger cardinals, saying that this incompleteness is indifferent to whether set theory is modeled in first- or second-order logic. First, we note that, as we have discussed, second-order logic already admits of uncountable sets, and so any conclusion or decision drawn on the basis of second-order logic’s use of uncountable sets will be logically flawed, and thus invalid. The reason these two types of incompleteness seem somehow different from each other is that the problem of Suslin lines is one that, like CH, is based on the flawed conception of uncountable infinity, and so as long as we do not recognize the flaw for what it is there will always remain a level of opaqueness and intractability regarding the nature of the incompleteness represented by Suslin lines; and also that, if we restrict ourselves to CH and ignore generalized CH, CH and Suslin’s Problem are about specific levels in the hierarchy of infinities, so that a system of logic that has these particular levels built in will be able to “make definitive statements” about CH and Suslin’s Problem. By contrast, the incompleteness in the case of ever greater cardinals always being possible is nothing but the brief shining of an oblique spotlight onto the never-ending nature of countable infinity. Yes, the elements involved represent uncountable infinities themselves, but the point is that they are treated as if they were finite, i.e., they are lined up in order of fixed magnitude in the same way that finite numbers can be; the understanding that the finite numbers themselves never end is thus, albeit weakly and indirectly, accentuated, disguised as a conclusion about the supposed hierarchy of uncountable infinities, and we therefore appear to be confronted with an unending sequence of finitized infinities. But, as we have stated, the never-ending nature of this sequence is not something that is special to sequences of transfinite numbers or to uncountable infinity. Rather, it is the true nature of infinity as such, that is, it is an expression of the fact that the countable numbers themselves never end, and so it is impossible to go beyond them. It is just that this example is an expression of this fact in the context of uncountable infinity, and so we feel more comfortable in directly addressing the issue and trying to understand its implications than we would in the case of the natural numbers themselves – if we address this issue too seriously in the context of the natural numbers themselves, we run the risk of finding legitimate reasons to question the entirety of set theory’s modern understanding of the infinite, and this understanding is simply too big and to emotionally gratifying a prize to risk losing.
Potter further states that “the incompleteness exemplified by Souslin’s hypothesis marks no mere inattention on our part in formulating the axioms: it is an inevitable consequence of the decision to restrict our attention to theories which are capable of being fully formalized.”123 He then points to Gödel’s incompleteness theorems to conclude that because there are statements that are true in any sufficiently strong consistent formal axiomatic system which are unprovable within the system, this explains why Suslin’s hypothesis cannot be decided within formal axiomatic set theory. There is some vagueness here. Why exactly would Suslin’s hypothesis qualify as a true statement that can be made in axiomatic set theory that cannot be proved true in the context of axiomatic set theory? But regardless, we already understand that this argument does not get to the heart of the matter of why Suslin’s hypothesis cannot be decided. It cannot be decided because it is based on logically flawed conceptions, and thus is meaningless as stated, while at the same time masquerading as a meaningful question. Potter then tells us, “So, for realists at least, it is inevitable that a first-order theory will not exhaust the claims about sets that we are, on reflection, prepared to accept as true… . The central difference between first- and second-order theories of sets lies … in the fact that the first-order axiom scheme of separation falls far short of expressing all the instances of the second-order axiom that the platonist would be willing to accept. The first-order axiomatization therefore does not characterize the operation which takes us from one level in the hierarchy to the next… . [It] amounts to much the same to say that the axiomatization fails to capture the operation that takes a set to its power set… . [The question of the cardinality of the set produced by the power set operation] is not settled by any of the first-order theories we have been discussing, and hence is an instance of the same sort of incompleteness as Souslin’s hypothesis.”124 Of course, Potter is correct that Suslin’s hypothesis and CH are examples of the same sort of incompleteness, but this is not because first-order logic in inherently limited in what it can prove regarding sets or the nature of reality or logical necessity as compared to the supposedly valid conceptions of second- and higher-order logic. It is because Suslin’s Problem and CH are both logically meaningless questions about specific higher levels of infinity, and so cannot be decided at all. Regarding the sets that a set theorist would be willing to accept as existing, this depends on the assumptions upon which the theorist in question bases his thinking about sets. If the theorist already assumes that uncountable sets exist and that it is not a logical error to finitize the infinite, then he will be willing to accept many more sets as existing than would a theorist who recognizes the logical error in these assumptions. Once we recognize that there is no such thing as uncountable infinity, and that if we are to fully understand the nature of countably infinite sets we must think of them in a way that does not conflate the finite with the infinite, then there is no problem at all to be solved with regard to how to understand the power set operation, since we would then understand that it only makes sense to take the power set of (a) a finite set of elements, whose cardinality we may increase to any finite number we like, or (b) a countably infinite set of elements, but with the restriction that since the original set is never a completed thing, the power set operation on this set can itself never be completed, and thus, even though the collecting of elements of the countably infinite set into the set elements of the power set is a logically valid operation, the power set itself, being a countably infinite set, cannot logically be a completed entity. Any proposal or effort to use second- or higher-order logic to attempt to fully understand the power set operation, or to resolve Suslin’s hypothesis, is an artifact of the flawed assumption that the uncountably infinite exists. Correct this flaw, and we find that we no longer need to appeal to higher-order logics to fully understand or capture the power set operation or the cardinalities (or lack thereof) of the resulting sets, or to resolve Suslin’s hypothesis.
The axiom of foundation states that all sets are well-founded, meaning that not only do such sets contain no logical contradictions, such as that in Russell’s paradox, but there are also no infinite regresses within any of their elements. This is the typical type of set studied in set theory. But Hrbacek tell us, “Nevertheless, alternatives allowing non-well-founded sets are logically consistent, have a certain intuitive appeal, and lately have found some applications… . An alternative intuitive view of sets is that the objects of which a set is composed have to be definite and distinct when the set is ‘finished,’ but not necessarily beforehand. They may be formed as part of the same process that leads to the collection of the set. A priori this does not exclude the possibility that a set could become one of its own elements, perhaps even its only element.”125 Here we see a certain amount of recognition of the correct way to view an infinite set or collection, viz., not as a completed, finite, fixed, manipulable thing, but as an ever-increasing, ever-expanding, or ever-changing collection of entities. In Hrbacek’s discussion of non-well-founded sets, they provide an alternative definition of “set” to include “infinite regress” or “perpetual increase” or “perpetual change” within a single element, i.e., the concept of set is here extended from what it is in standard or typical set theory so that an inherent part of “element” is the possibility of being forever changing. This is why they put “finished” in quotes – such a set is forever changing, and thus can never actually be finished, complete, or whole. As Hrbacek state, such sets have “a certain intuitive appeal,” and this is not surprising given that such sets, so long as we restrict the nature of their infinity to the countable kind, are accurate representations of the true nature of infinity, i.e., an infinity of entities that can be matched one-to-one with the ever-increasing natural numbers, and thus whose representation or implementation of infinity is logically understandable. But as soon as we try to extend this infinite regress or permanent change that is proposed to take place within these sets into the realm of the uncountable, then we will have begun another flight into the permanently obscure and intractable, because uncountable infinity is a logically nonsensical concept. One may imagine new questions arising with regard to uncountable non-well-founded sets, e.g., the question of the nature of an uncountable infinite regress within a single element of a given non-well-founded set, that, like CH or Suslin’s Problem, persist for decades or more because no one wishes to admit that there are logical flaws at the foundation of such questions which make the questions logically nonsensical, and thus inherently non-answerable.
However, Hrbacek do not go far enough: they do not recognize the essential sameness between these so-called non-well-founded sets, on the one hand, and the more “normal” type of infinite set, such as ℕ, ℚ, or ℝ, on the other. In the latter cases, as we have discussed, such a sequence or collection of elements can also never be complete, and the reason there is a certain “intuitive appeal” for treating these “normal” infinite sets as finished or fixed or finite in certain ways is precisely the same reason as for non-well-founded sets, viz., that in both cases, so long as we correctly understand the nature of infinity, all components involved are countable, and thus intuitively understandable. A correct understanding of infinity allows us to treat non-well-founded sets that contain no logical contradictions no differently than we treat the “normal” countably infinite sets with which set theory is already familiar, and eliminates the mystique that surrounds non-well-founded sets and that encourages us to treat them as some kind of “special” thing or entity which has a “special” status among sets. And in the case of sets whose definitions contain a logical contradiction, such as, in Russell’s paradox, a set that contains all and only the sets that do not contain themselves, these sets would be excluded from consideration on the ground that it is impossible, because logically contradictory, for either a finite or a countably infinite set to exist which satisfies such a requirement – such a definition is like asking whether there can exist an irresistible force that could meet an immovable object. But, of course, such a situation could not exist, because the statement contains a logical contradiction. We may create grammatically correct sentences that make use of well-understood concepts, but if these concepts are put together in the right way they postulate a thing or process that could not be. The fact that we can imagine these concepts “fitting” together in the way in which the logically contradictory statement says that they should fit together is an artifact of our minds’ glossing over the conflation of two fundamentally different or opposing things, because such conflation may be practically beneficial in various real-life contexts which only require an approximate understanding of reality. In fact, this is a built-in evolutionary tendency, and so it is often difficult to overcome. And it is this same tendency that allows us to conflate the finite and the infinite in set theory and gloss over the fact that these two things are fundamentally different. Actual logical contradictions in the creation of sets, such as that described in Russell’s paradox, have the same logical status as the logical errors that we have been discussing, i.e., the conflation of the finite and the infinite and the assumption that there are multiple levels of infinity; in all these cases there is a logical flaw in the reasoning, and thus the concept being reasoned about will permanently resist our efforts to understand it.
We note here that invoking concepts such as “fuzzy logic” to say, in the case of Russell’s paradox, that an element can be formally specified as both being in a set and not being in the set at the same time, or the quantum mechanical superposition of states to try to say the same thing, is grasping at straws. Fuzzy logic is nothing more than an alternative way to express the concept of probability, and as such does not have a real claim to be an instantiation or expression of logic at all, which deals with logical necessity and logical contradiction, i.e., definitive things, not probabilistic things. And the concept of the quantum superposition of states is only superficially similar to an element being in a set and not in the set at the same time. Superficial similarities between two things are often mistaken for essential similarities, and we must always be on the lookout for such conflation in our own thinking. If a set is supposed to “either contain an element or not contain the element,” then, well, it either contains the element or it does not. There is no third option, and, by the definition of set, the idea of a single element being both in a set and not in it at the same time is explicitly excluded, and so not possible. One may redefine “set” to include this allowance, but of what value is this redefinition? Does it clarify anything or add to our understanding? Or does it just muddy the waters further? In fact, there is, as mentioned above, a logical contradiction inherent in such a concept, since a single “element” is supposed to be a fixed, finite, unchanging thing, and if this “element” is both entirely within a set and entirely outside of it at the same time, this creates a logically nonsensical state of affairs and thus a permanent opaqueness and intractability when it comes to our ability to understand the resulting arrangement, in the same way that CH and Suslin’s Problem do. Remove the logical contradictions from our thinking, and things suddenly become clear and understandable.
In talking about “grounded” sets, i.e., sets that contain no infinite membership regress within any of their elements and thus whose nested membership relations always stop after a finite number of steps – i.e., “well-founded” sets as we have been using this term – and the debate over the extent of sameness or difference between a set and a collection, Potter states, “Most of those who [attempt to argue that every collection is a set] draw attention to the difficulty of conceiving of an ungrounded collection. Suppes (1960, p. 53) simply challenges the reader who doubts this to try to come up with an example. Mayberry (1977, p. 32) suggest that ‘anyone who tries … to form a clear picture of what a non-well-founded collection might be … will see why extensionality forces us to accept the well-foundedness of the membership relation.’ Drake (1974, p. 13) stigmatizes ungrounded collections as ‘strange’ and says it is ‘difficult to give any intuitive meaning’ to them.”126 But the discussion above in this section makes it clear that infinite membership regress within a single set or an element of a set is no more difficult to grasp than the infinite sequence (or infinite “progress”) of the natural numbers, the rationals, or the real numbers when they are correctly understood as countable. In all cases we are simply dealing with the concept of countable infinity; the guise is just different for each, and in some cases, such as the natural numbers, it is easier to recognize the nature of the finite pattern that produces the never-ending progression than it is in other cases. We may also say that any acceptance by Drake, Mayberry, Suppes, and others of the same opinion regarding non-well-founded sets, of the supposed logical validity of the concept of uncountable infinity could easily be a detriment to their understanding of, and their thoughts and ideas regarding, other aspects or examples or representations of infinity, and make it harder for them to clearly conceive of the true nature of infinity and harder to see when their thoughts about infinity are based partly or wholly on a logical contradiction.
Hrbacek introduce the “Axiom of Anti-Foundation,” which states that “every graph has a unique decoration.”127 By graph is meant a network of vertices and directed edges as in graph theory, where the directed edges represent membership relations between sets and elements and the vertices represent the sets and elements being related. A decoration is essentially the fleshing or tracing out of the graph by determining the neighbor vertices of each given vertex. The axiom of anti-foundation modifies the axiom of foundation – which says that all sets are well-founded, and which thus implies that the only graphs possible are ones for well-founded sets – by dropping the requirement that graphs must represent only well-founded sets. As such, graphs can have directed edges that reverse the membership direction, so that an element can point to its parent, or a parent of its parent, etc., which means that these graphs can represent sets which contain themselves or one or more of their parents;128 and the axiom of anti-foundation says that all such graphs in this extended universe of graphs have unique decorations. But recall our discussion earlier that when we try to enumerate all elements within such a set, we cannot, because in order for the set to avoid logical contradiction it must contain within it a countably infinite regress. In particular, consider any set that contains itself, such as the so-called reflexive sets, for which, e.g., X = {X}.129 This is represented in a decorated graph by X at a vertex and a directed edge starting at X and circling back around to X. But, as we discussed earlier, a set that contains an element that is a complete or finished copy of the set itself is impossible because the attempt to create such a set leads to an infinite regress. Therefore, such concrete representations of reflexive sets, which show a simple, finite equation or a vertex of a graph looping back on itself, or other such tricks which show in concrete, finite, complete terms a set which contains itself or one or more of its parents, are examples of the finitizing of the infinite, and thus if, e.g., X is treated as being the same mathematical object on both sides of the equation or both sides of the directed edge, this is a logical error and will produce logically flawed results in mathematical arguments which use this treatment. If, on the other hand, the X on the left of the equation, or at the start of the directed edge, is treated as a label or identifier of the set containing a set X, then there is no logical contradiction; but if we do this, we can no longer treat our expression, or our graph, as being a depiction of the idea of set which contains itself, and it is therefore misleading to present it as such. We should also note that the concept of self-reference and the concept of a set which contains itself are similar in certain ways, but this similarity has its boundaries. A thing can make reference to itself and yet not be a member of itself as a set. Just because a set which contains itself makes use of the concept of self-reference does not mean that any use of the concept of self-reference must be applicable to and logically valid in the context of the concept of a set which contains itself. In using, e.g., directed graphs as examples of self-reference, we cannot simply conclude that what is true about them must be true about sets which contain themselves and whose membership relations match the vertex relations in a given graph. In particular, just because it is logically meaningful to use directed graphs with fixed vertices to model the concept of self-reference in certain things, such as programs that take other programs, or themselves, as inputs,130 does not mean that the concept of a static or completed set which contains itself is a logically valid conception. This is to make the same logical error that Cantor made in the diagonal argument, whereby a false equality, that between infinite decimal sequences and the finite, fixed numbers which they approach, led him to erroneously conclude that what is (or seems) true about a list of infinite decimal sequences must also be true about a list of their finite, fixed limit points. The fact that there is self-reference in certain types of directed graphs as well as in the concept of a set which contains itself does not mean we are justified in saying that the use of self-referential directed graphs in other areas of investigation is an application of the concept of non-well-founded sets. In fact, it is not. Such directed graphs are expressions of self-reference in the context of static entities; a non-well-founded set is an expression of self-reference that, in order to avoid logical contradiction, must be ever-changing, and thus never static. In saying that the one is an application of the other, we do a disservice to our effort to understand infinity, by making the concept of finitized infinity seem that much more legitimate.
Feferman states the following:
Cohen’s method of forcing and generic extensions of models of set theory opened the floodgates for a veritable deluge of relative consistency and independence results, to begin with his own theorem that it is consistent with ZFC that the cardinality 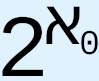 of the continuum can equal
of the continuum can equal 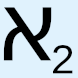 ; in fact by the same methods, it can be made as large among the alephs as one pleases.131
; in fact by the same methods, it can be made as large among the alephs as one pleases.131
Right away we can see that something is amiss here. “Forcing” is the method invented by Paul Cohen and used in his 1963 paper to prove that CH cannot be proved from the axioms of ZFC. It is interesting that the method of forcing, which is now a commonly-accepted tool among set theorists and is seen as a powerful method of deriving results and theorems, can be used to prove that the cardinality of the continuum, i.e., the total “quantity” or “number” of real numbers, is simultaneously equal to any and all of an infinite number of different cardinalities. Isn’t the set of real numbers supposed to be a “completed totality”? How is it possible then that this set can have 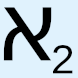 elements, but also at the same time
elements, but also at the same time 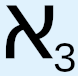 ,
, 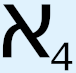 ,
, 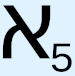 , etc., elements? This is like saying the complete set {1, 2, 3} not only has 3 elements, but at the same time has 4, 5, 6, and, indeed, all possible numbers of elements. This makes no sense. One may object that things behave differently in the realm of infinite sets in certain ways; for example,
, etc., elements? This is like saying the complete set {1, 2, 3} not only has 3 elements, but at the same time has 4, 5, 6, and, indeed, all possible numbers of elements. This makes no sense. One may object that things behave differently in the realm of infinite sets in certain ways; for example, 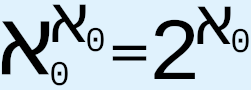 , or
, or 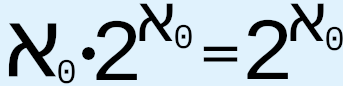 .132 But this does nothing to make things clear, and instead only begs the question. The real question is why exactly should things behave differently in the realm of the infinite? It does not help to bring to bear the idea that cardinal and ordinal arithmetic are well-defined, because this answer rests on the definitions, and on the extensions of procedures defined in the realm of the finite, which we have agreed upon, not on logically necessary requirements. One may also say that the forcing results are evidence that CH is false, because CH restricts the cardinality of the continuum to the first uncountable cardinal. But we have seen that this also is not a valid response, because it does not understand that CH cannot be either true or false since it is based on logically flawed conceptions, and is therefore not a meaningful statement. In fact, this result, that forcing can make the cardinality of the continuum equal to any aleph no matter how large, is an example of pathological behavior which results from the ideas involved being based on, and intermingled with, the logical error of the conflation of the finite with the infinite. Once we recognize the error, results such as this disappear. But then, so do opportunities to show one’s mathematical and philosophical peers that one has a deep grasp of the detailed inner structure of infinity.
.132 But this does nothing to make things clear, and instead only begs the question. The real question is why exactly should things behave differently in the realm of the infinite? It does not help to bring to bear the idea that cardinal and ordinal arithmetic are well-defined, because this answer rests on the definitions, and on the extensions of procedures defined in the realm of the finite, which we have agreed upon, not on logically necessary requirements. One may also say that the forcing results are evidence that CH is false, because CH restricts the cardinality of the continuum to the first uncountable cardinal. But we have seen that this also is not a valid response, because it does not understand that CH cannot be either true or false since it is based on logically flawed conceptions, and is therefore not a meaningful statement. In fact, this result, that forcing can make the cardinality of the continuum equal to any aleph no matter how large, is an example of pathological behavior which results from the ideas involved being based on, and intermingled with, the logical error of the conflation of the finite with the infinite. Once we recognize the error, results such as this disappear. But then, so do opportunities to show one’s mathematical and philosophical peers that one has a deep grasp of the detailed inner structure of infinity.
We may also say that the idea that 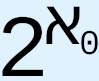 can be equated to any of the infinite number of uncountable cardinals is a symptom of the same underlying logical error that makes us think that an uncountable set should have positive measure. If no matter how many zero-length points we accumulate, the length of the line thus accumulated will always still be 0, and therefore it is a logical contradiction to say that by such point accumulation it is possible to build up a non-zero, positive Euclidean length measure, then it is not surprising that set theory has come up with a “result” that says that the cardinality of the reals can be greater than any uncountable cardinal. After all, the cardinality of the reals is supposed to be an infinite number, which is, of course, greater than 0 in magnitude, and so under this conception of the reals we must make the impossible leap to assuming as valid the logical contradiction of zero-length points building a non-zero, positive Euclidean measure in order to have even a hope of determining the “correct” value for the cardinality of the reals. But at the same time, the list of transfinite and uncountable ordinals is treated as if these ordinals were finite numbers that could be fixed and could be listed together in a set in order of increasing magnitude. On the one side, we have made that which will always be nothing into something, and on the other side we have made that which is so infinite that it is literally beyond understanding into something that is finite and circumscribable, i.e., into a thing which takes on the only essential characteristic of a finite number. By overlaying the one upon the other, it is not hard to see how it would not be difficult to conclude that something that is so great that it can overcome even the logical contradiction that nothing can never be something in order to actually make something out of nothing, could be great enough to be greater than any of the finitized uncountable infinities that we have listed in increasing order of magnitude in a set and learned to treat in essential ways as if they were finite numbers or entities. Note that we are not saying here that Cohen’s method of “forcing” proves that the cardinality of the reals is greater than that of any other uncountable infinity. The point is that by properly massaging the ideas, we can force them to fit the mold we wish they had, and prove essentially any result we desire; and by calling these modified and molded ideas by the same names as they had before, such as calling a finite symbol that is used in a linear sequence of magnitudes an instance of “uncountable infinity,” we mask to ourselves the conceptual changes that we have made for the purpose of drawing particular, desired conclusions. The point can be made here again that when we have already assumed that a logically flawed idea is valid, we are freer to manipulate and massage and remold the ideas with which we deal than we would otherwise be, and this can produce all sorts of results that could not be otherwise produced, since under such a loosening of constraints logically invalid or nonsensical results can be made to, at least in a formal sense, appear logically valid, and so a conclusion need not be considered less worthy or less likely to be true simply because we seem to be at a permanent loss as to how to find a way to clearly understand its nature, significance, and basic meaning.
can be equated to any of the infinite number of uncountable cardinals is a symptom of the same underlying logical error that makes us think that an uncountable set should have positive measure. If no matter how many zero-length points we accumulate, the length of the line thus accumulated will always still be 0, and therefore it is a logical contradiction to say that by such point accumulation it is possible to build up a non-zero, positive Euclidean length measure, then it is not surprising that set theory has come up with a “result” that says that the cardinality of the reals can be greater than any uncountable cardinal. After all, the cardinality of the reals is supposed to be an infinite number, which is, of course, greater than 0 in magnitude, and so under this conception of the reals we must make the impossible leap to assuming as valid the logical contradiction of zero-length points building a non-zero, positive Euclidean measure in order to have even a hope of determining the “correct” value for the cardinality of the reals. But at the same time, the list of transfinite and uncountable ordinals is treated as if these ordinals were finite numbers that could be fixed and could be listed together in a set in order of increasing magnitude. On the one side, we have made that which will always be nothing into something, and on the other side we have made that which is so infinite that it is literally beyond understanding into something that is finite and circumscribable, i.e., into a thing which takes on the only essential characteristic of a finite number. By overlaying the one upon the other, it is not hard to see how it would not be difficult to conclude that something that is so great that it can overcome even the logical contradiction that nothing can never be something in order to actually make something out of nothing, could be great enough to be greater than any of the finitized uncountable infinities that we have listed in increasing order of magnitude in a set and learned to treat in essential ways as if they were finite numbers or entities. Note that we are not saying here that Cohen’s method of “forcing” proves that the cardinality of the reals is greater than that of any other uncountable infinity. The point is that by properly massaging the ideas, we can force them to fit the mold we wish they had, and prove essentially any result we desire; and by calling these modified and molded ideas by the same names as they had before, such as calling a finite symbol that is used in a linear sequence of magnitudes an instance of “uncountable infinity,” we mask to ourselves the conceptual changes that we have made for the purpose of drawing particular, desired conclusions. The point can be made here again that when we have already assumed that a logically flawed idea is valid, we are freer to manipulate and massage and remold the ideas with which we deal than we would otherwise be, and this can produce all sorts of results that could not be otherwise produced, since under such a loosening of constraints logically invalid or nonsensical results can be made to, at least in a formal sense, appear logically valid, and so a conclusion need not be considered less worthy or less likely to be true simply because we seem to be at a permanent loss as to how to find a way to clearly understand its nature, significance, and basic meaning.
Also, in talking about the use of large cardinal axioms to try to find a way to prove or disprove CH, Feferman tells us that “by the work of Levy and Solovay (1967), CH is independent of every extension of ZFC by large cardinal axioms of either kind [i.e., either small large cardinals or large large cardinals] if the extension is consistent at all, the biggest nail in the coffin so far.”133 Isn’t this interesting. If there is a logical error at the root of CH, then, of course, it will be impossible to prove that CH is true, or false, on the basis of any set of axioms that are supposed to be an accurate model, or part of such a model, of the inherent rationality of the real world. But as we have seen, this logical error is the same logical error that makes the concept of an infinite cardinal, or multiple levels of infinite cardinals with different cardinalities, inherently opaque, and thus meaningless. Therefore, adding axioms to ZFC that say that certain “even larger” large cardinals exist will never do anything to either prove or disprove CH; all they will do is add to the mire of confusion and intractability, while at the same time convincing us, since we allow ourselves to be convinced, that even though we have not yet solved the problem, at least we now understand “the structure of infinity” a little better than we did before. But infinity itself has no structure. Sets whose elements are defined by a particular rule that allows for the number of elements in the set to keep growing, such as the naturals or rationals, have structure, i.e., relations or patterns among their elements. But infinity itself is not a “thing” which can have structure. Infinity is nothing but the quality of increasing without bound. A recognition that no large cardinal axiom, however “great” the cardinal in question, can ever be added to ZFC to prove or disprove CH is, in a certain roundabout way, a step in the right direction.
In discussing the equiconsistency of different versions of set theory that “are based on independently motivated and conceptually distinct principles,” Feferman states that Woodin refers to three different set theories, “ZFC + SBH, ZF + AD, and ZFC + ‘There exist infinitely many Woodin cardinals,’ of which it has been shown that they are equiconsistent, with the third of these providing the essential link in the proof.”134 In a footnote, he states, “SBH abbreviates the Stationary Basis Hypothesis; cf. Woodin (2011) p. 450. Shelah (1986) proved that SBH implies that CH is false.”135 What we have here, then, is a result which seems to provide support to the idea that CH is false, taking SBH as an axiom. But notice that the concept of “infinitely many Woodin cardinals,” where a Woodin cardinal is a type of large, which implies uncountable, cardinal, is “the essential link in the proof.” Once again, we make essential use of concepts based on the logical error of conflating the finite with the infinite in order to produce a result, specifically that these three independently-developed versions of set theory are “equiconsistent,” and that, thus, the idea that CH is false is bolstered by “independent confirmation.” But as with the arguments that prove CH is true, or those that prove CH is false by equating 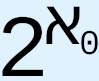 with a different level of uncountable infinity, or with multiple such levels, or by saying that
with a different level of uncountable infinity, or with multiple such levels, or by saying that 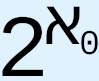 is not an aleph, these arguments and conclusions are only relevant in the context of ideas that already assume that it is logically valid to equate the finite with the infinite. As such, these arguments never get to the heart of the matter. At most, they skirt the issue while pretending to provide meaningful results. Any argument based on a logical error will not be able to solve any problem, including problems such as CH whose solution depends on the direct recognition that the logical error is a logical error. Such arguments ultimately only perpetuate the confusion regarding why the problem, after so many years of effort, still has not found a satisfactory resolution.
is not an aleph, these arguments and conclusions are only relevant in the context of ideas that already assume that it is logically valid to equate the finite with the infinite. As such, these arguments never get to the heart of the matter. At most, they skirt the issue while pretending to provide meaningful results. Any argument based on a logical error will not be able to solve any problem, including problems such as CH whose solution depends on the direct recognition that the logical error is a logical error. Such arguments ultimately only perpetuate the confusion regarding why the problem, after so many years of effort, still has not found a satisfactory resolution.
In discussing the mathematical status of CH, i.e., whether it is or should be considered an actual mathematical problem, rather than, e.g., one of metamathematics or philosophy, Feferman makes this comment with regard to Gödel’s view on the subject: “Of course there are those like Gödel and a few others for whom there is no ‘duck’ problem; on their view, CH is definite and we only have to search for new ways to settle it, perhaps by other means than large cardinal axioms.”136 Feferman also quotes Gödel from 1947: “Cantor’s continuum problem is simply the question: How many points are there on a straight line in Euclidean space? In other terms, the question is: How many different sets of integers do there exist? ... [t]he analysis of the phrase ‘how many’ leads unambiguously to quite a definite meaning for [this] question ... namely, to find out which one of the 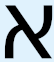 's is the number of points on a straight line.”137 Gödel’s views have been discussed to an extent elsewhere in this paper, in particular in the section on the axiom of constructibility. The comment to be made here is just that Gödel seems to have been a person for whom obtaining absolute certainty was of paramount importance, but for whom the usual route to certainty for humans, viz., blind religious belief, ignorance, distraction, and routine, was not appropriate or satisfying; however, if we are not careful, this deeper intellectual mentality can set up roadblocks and blind spots, sometimes powerful, in the way of our rational understanding of things as psychological and emotional protection against the more unpleasant aspects of reality. This appears to have been the case with Gödel, and though, of course, he has published some influential results, and, of course, he was intelligent, we must not let these things deter us from acknowledging any flaw that might exist in his reasoning, about set theory or about anything else that might be relevant to our investigations. On the basis of what we have learned in the present paper, we may conclude that Gödel was wrong in assuming that CH could be solved, i.e., could be proven true or false, and that we had up to that point simply not found the proper way to provide a proof. In fact, CH cannot be proven true or false in any way that does not already depend on the assumed validity of the logical error of conflating the finite and the infinite. Without this assumption, i.e., on the basis of nothing more than universal logical validity and necessity, CH is not a meaningful statement, and so cannot be assigned a truth value.
's is the number of points on a straight line.”137 Gödel’s views have been discussed to an extent elsewhere in this paper, in particular in the section on the axiom of constructibility. The comment to be made here is just that Gödel seems to have been a person for whom obtaining absolute certainty was of paramount importance, but for whom the usual route to certainty for humans, viz., blind religious belief, ignorance, distraction, and routine, was not appropriate or satisfying; however, if we are not careful, this deeper intellectual mentality can set up roadblocks and blind spots, sometimes powerful, in the way of our rational understanding of things as psychological and emotional protection against the more unpleasant aspects of reality. This appears to have been the case with Gödel, and though, of course, he has published some influential results, and, of course, he was intelligent, we must not let these things deter us from acknowledging any flaw that might exist in his reasoning, about set theory or about anything else that might be relevant to our investigations. On the basis of what we have learned in the present paper, we may conclude that Gödel was wrong in assuming that CH could be solved, i.e., could be proven true or false, and that we had up to that point simply not found the proper way to provide a proof. In fact, CH cannot be proven true or false in any way that does not already depend on the assumed validity of the logical error of conflating the finite and the infinite. Without this assumption, i.e., on the basis of nothing more than universal logical validity and necessity, CH is not a meaningful statement, and so cannot be assigned a truth value.
In Hrbacek’s discussion of the exponentiation of cardinals, they say that it is “simple” to add and multiply cardinals, but that “the evaluation of cardinal exponentiation is rather complicated. Here we do not give a complete set of rules (in fact, in a sense, the general problem of evaluation of κλ is still open), but prove only the basic properties of the operation κλ … . Without assuming the Generalized Continuum Hypothesis, there is not much one can prove about 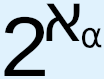 except [two trivial properties based on Cantor’s Theorem, which says that the magnitude of a power set is greater than the magnitude of the original set].”138 But we can understand the reason for these limitations that Hrbacek express in light of what has been said in this paper. The difficulty of understanding cardinal exponentiation is not due to the fact that we just haven’t found the “right way to think about it,” but to the fact that it makes no logical sense to raise either a finite or an infinite number to an infinite power. Cardinal addition and multiplication are “easy” to understand because it is an easy thing to carry over these operations that make sense on finite quantities into the realm of the transfinite once we make the leap and conclude (erroneously) that infinite quantities can be represented by finite symbols that can be mathematically manipulated as if they were finite. But the leap that is necessary to overcome the logical error of the conflation of the finite and the infinite is much greater when it comes to exponentiation of cardinals, because then we have added another layer of infinity, since we are now supposed to be able to multiply an infinite number an infinite number of times. It may someday be the case that set theorists will have settled on an agreed-upon set of rules for cardinal exponentiation, though I will not hold my breath. But all this would mean is that they would have found a way to collectively gloss over the logical error of conflating the finite with the infinite even at this more difficult level, i.e., they would have collectively made the greater leap necessary to do this. The logical error would still be present, in no greater or less capacity than it was before; it would simply be that, as is the case with the supposed difference between countable and uncountable infinity, there would now be an agreed-upon and customary way to ignore it, and so it would be easier to ignore. Also, when Hrbacek state, in the context of the exponentiation of cardinals, that not much can be said about
except [two trivial properties based on Cantor’s Theorem, which says that the magnitude of a power set is greater than the magnitude of the original set].”138 But we can understand the reason for these limitations that Hrbacek express in light of what has been said in this paper. The difficulty of understanding cardinal exponentiation is not due to the fact that we just haven’t found the “right way to think about it,” but to the fact that it makes no logical sense to raise either a finite or an infinite number to an infinite power. Cardinal addition and multiplication are “easy” to understand because it is an easy thing to carry over these operations that make sense on finite quantities into the realm of the transfinite once we make the leap and conclude (erroneously) that infinite quantities can be represented by finite symbols that can be mathematically manipulated as if they were finite. But the leap that is necessary to overcome the logical error of the conflation of the finite and the infinite is much greater when it comes to exponentiation of cardinals, because then we have added another layer of infinity, since we are now supposed to be able to multiply an infinite number an infinite number of times. It may someday be the case that set theorists will have settled on an agreed-upon set of rules for cardinal exponentiation, though I will not hold my breath. But all this would mean is that they would have found a way to collectively gloss over the logical error of conflating the finite with the infinite even at this more difficult level, i.e., they would have collectively made the greater leap necessary to do this. The logical error would still be present, in no greater or less capacity than it was before; it would simply be that, as is the case with the supposed difference between countable and uncountable infinity, there would now be an agreed-upon and customary way to ignore it, and so it would be easier to ignore. Also, when Hrbacek state, in the context of the exponentiation of cardinals, that not much can be said about 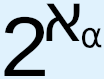 without first assuming as true generalized CH, this is not by coincidence. It is because
without first assuming as true generalized CH, this is not by coincidence. It is because 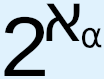 , and cardinal exponentiation in general, are logically nonsensical, so the only way to feel as if we are able to move forward in “understanding” cardinal exponentiation is by first arbitrarily assuming an initial nonsensical relation between different levels of infinity, and then basing our further investigations on that. Indeed, as Hrbacek state, “the Generalized Continuum Hypothesis greatly simplifies the cardinal exponentiation; in fact, the operation κλ can then be evaluated by very simple rules.”139
, and cardinal exponentiation in general, are logically nonsensical, so the only way to feel as if we are able to move forward in “understanding” cardinal exponentiation is by first arbitrarily assuming an initial nonsensical relation between different levels of infinity, and then basing our further investigations on that. Indeed, as Hrbacek state, “the Generalized Continuum Hypothesis greatly simplifies the cardinal exponentiation; in fact, the operation κλ can then be evaluated by very simple rules.”139
Also, Hrbacek state, “Persistent failures of all attempts [to solve problems such as CH or Suslin’s Problem] led some mathematicians to suspect that they cannot be solved at all at the current level of mathematical art… . Undecidability of the Continuum Hypothesis on the basis of our present understanding of sets as reflected by the axioms of ZFC means that some fundamental property of sets is still unknown. The task is now to find this property and formulate it as a new axiom which, when added to ZFC, would decide CH one way or another.”140 But this is not the correct approach. The difficulty with solving these outstanding problems is, as we have seen, not the result of our lack of knowledge regarding some aspect or another of sets, so that when this knowledge is gained the confusion will clear and we will finally be able to assign a truth value to these statements; rather, it is the result of the fact that these statements are not logically meaningful, and thus can never be assigned a truth value. The way to solve such problems is to recognize the logical error on which they are based, correct the logical error, and thereby show that the problems themselves are only illusions.
Hrbacek further state that “there appears to be very little evidence that the axiom 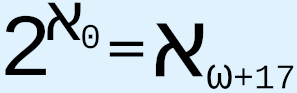 (or any other axiom of the form
(or any other axiom of the form 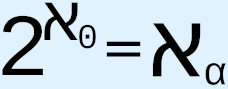 ) satisfies” the two basic and reasonable requirements that the axiom (a) postulate something that we can clearly and intuitively recognize as logically valid, and (b) have useful and fruitful consequences in other areas of mathematics.141 They state further, “In fact, no axioms that would be intuitively obvious in the same way as the axioms of ZFC have been proposed. Perhaps our intuition in these matters has reached its limits.”142 However, the only way our intuition can reach a fundamental or constitutively insurmountable limit is if we try to intuit, to understand, something that is based on or contains a logical contradiction. If something we are trying to understand does not contain and is not based on a logical contradiction, then there is no fundamental limit to our ability to intuit or understand it. There may be practical limits, such as those caused by our technical or financial, etc., inability to gather necessary data about the phenomenon we are trying to understand, or by our own biases and emotional interests that, depending on the person, may forever prevent a particular individual from coming to a clear understanding of something that is logically valid. But there is no such thing as a “fundamental limit” to the human psyche’s ability to understand the universe, such that we are constitutively incapable as thinking organisms or as a species of perceiving or conceiving of or comprehending things about reality or existence beyond this point.143 We do not need to “learn to accept our limitations” in this arena, but rather to recognize that when we consistently fail to answer a question or solve a problem despite many years or decades of serious attempts, one possible reason for this is that the problem we are trying to solve or the question we are trying to answer is a red herring, i.e., one that seems like a meaningful statement, but actually is not, because the statement is based on a hidden logical error. The reason no intuitively obvious or acceptable axioms have been proposed to account for CH and other such outstanding problems is that these problems are illogical, and therefore no logically valid or intuitively acceptable axiom can ever be proposed to account for them or accommodate them.
) satisfies” the two basic and reasonable requirements that the axiom (a) postulate something that we can clearly and intuitively recognize as logically valid, and (b) have useful and fruitful consequences in other areas of mathematics.141 They state further, “In fact, no axioms that would be intuitively obvious in the same way as the axioms of ZFC have been proposed. Perhaps our intuition in these matters has reached its limits.”142 However, the only way our intuition can reach a fundamental or constitutively insurmountable limit is if we try to intuit, to understand, something that is based on or contains a logical contradiction. If something we are trying to understand does not contain and is not based on a logical contradiction, then there is no fundamental limit to our ability to intuit or understand it. There may be practical limits, such as those caused by our technical or financial, etc., inability to gather necessary data about the phenomenon we are trying to understand, or by our own biases and emotional interests that, depending on the person, may forever prevent a particular individual from coming to a clear understanding of something that is logically valid. But there is no such thing as a “fundamental limit” to the human psyche’s ability to understand the universe, such that we are constitutively incapable as thinking organisms or as a species of perceiving or conceiving of or comprehending things about reality or existence beyond this point.143 We do not need to “learn to accept our limitations” in this arena, but rather to recognize that when we consistently fail to answer a question or solve a problem despite many years or decades of serious attempts, one possible reason for this is that the problem we are trying to solve or the question we are trying to answer is a red herring, i.e., one that seems like a meaningful statement, but actually is not, because the statement is based on a hidden logical error. The reason no intuitively obvious or acceptable axioms have been proposed to account for CH and other such outstanding problems is that these problems are illogical, and therefore no logically valid or intuitively acceptable axiom can ever be proposed to account for them or accommodate them.
But Hrbacek do not seem to be proposing that we “accept our limitations” and leave it at that. Rather, they follow the above statement with commentary on the recent “great amount of research into [large cardinals] performed over the last 40 years [that] has produced the very rich, often very subtle and difficult theory of large cardinals, whose esthetic appeal makes it difficult not to believe that it describes true aspects of the universe of set theory.”144 They also state, “The typical pattern [in investigations of large cardinals and their relation to open questions in set theory] is that such questions can be answered one way assuming an appropriate large cardinal exists, and have an opposite answer assuming that it does not, with the answer obtained with the help of large cardinals being preferable in the sense of being much more ‘natural,’ ‘profound,’ or ‘beautiful.’”145 This is not the place for a detailed discussion of the psychological and emotional reasons why we might feel that something is natural, profound, or beautiful. But we can say here that the desire to finitize infinity, and thus, in a crude but powerful emotional sense, become immortal, that is, cheat death or solve the problem of mortality, from which all other problems and fears spring, is the most powerful and emotionally impactful drive in the human psyche, and this is because our psyche is produced by the process of biological evolution. The feeling that we have “further conquered” or “further mastered” the infinite by “solving” a problem related to uncountable infinity by the means of assuming the existence of an “even greater” uncountable cardinal than the ones we “knew” about before, can easily provide a great sense of resolution, if only a temporary one, with regard to our powerful need to overcome death; and it makes sense to say that our psyches are evolutionarily attuned to view such “solutions” as attractive, since they give us, in a crude but powerful emotional way, a sense that we are on the right track in solving the problem of our own mortality. After all, the effect of our feeling that we are attracted to something is that there is a greater chance that we will actively pursue it, to try to obtain or achieve it, and the effect that we are repulsed by something is that there is a greater chance that we will actively avoid it. Why, then, would the psyche not be built by the evolutionary process to be attracted to things that it feels may help it overcome the greatest problem with which it is faced, viz., its own mortality, its own finiteness, and to avoid things that it feels may increase its chances of mortality? In this way it makes sense that conclusions which make us feel like we are conquering or mastering the infinite can sometimes feel as if they are natural or profound or beautiful. But just as we can rationally perceive that solving a problem in set theory will not, in fact, make us immortal, we should understand that just because we feel that some-thing is natural or profound or beautiful does not necessarily mean that it is logically valid, i.e., correct. In this way, Hrbacek also fall into the trap of trying to connect a desire to conquer the infinite, and thus become immortal – again, in a crude but powerful emotional sense – which can make certain “results” regarding uncountable infinity seem natural, profound, or beautiful, with actual logical necessity. It is often the case that logically valid conclusions seem to us to be natural, profound, or beautiful,146 but, as would be said in propositional logic, the converse is not necessarily true just because the original conditional statement is true. The reason that we can sometimes feel this sense of naturalness or profundity or beauty with regard to results obtained by the use of large cardinals is a combination of (a) our evolutionarily built-in desire to conflate the finite with the infinite, so as to, in a crude but powerful emotional sense, overcome mortality, and (b) the fact that the treatment that we make of large cardinals and uncountable infinity in general is the result of such conflation, which allows the logically flawed concepts to masquerade as logically valid, and infinities to masquerade as finite things which can be manipulated by legitimate, i.e., logically valid, mathematical operations and procedures; the “results” of these flawed operations can seem natural, profound, or beautiful by psychological and emotional reference to our feeling of these same things for various actually logically valid mathematical results and conclusions, combined with our desire to conquer death. Our need to finitize the infinite makes us overlook the fact that it is logically impossible to do so, and this need is built into the human psyche by the evolutionary process.
But there is another way in which we may “accept our limitations” with regard to understanding infinity. We do not accept any limitation with regard to our ability to understand infinity. We simply accept our limitation with regard to our inability to overcome mortality. Once we accept this limitation, it becomes much easier to perceive and understand the logical flaws in any part of our thinking, with regard to set theory or anything else, because we no longer fear death, the most unpleasant of all unpleasant truths, in a blindingly powerful emotional way, and thus there is no further reason for the built-in psychological and emotional protection from this knowledge to present an insurmountable obstacle to our deeper rational understanding of the world. Such unconditional protection no longer being needed, it will begin to fall away of its own accord, even as we continue actively pursuing a deeper rational understanding of things and thus actively making it easier for such protection to continue falling away, with the result that we are able to ever more clearly see the objective nature of reality.
Hrbacek state, “It is known that the existence of inaccessible cardinals cannot be proven in ZFC … .”147 This is not surprising, since inaccessible cardinals are defined such that they are examples of uncountable infinity, which (a) is a logically contradictory concept, and (b) cannot be built up out of countable infinity, which is the conception of infinity used in ZFC (in particular the axiom of infinity and the axiom of countable choice) and urged onto the extension of ZFC into the transfinite by the finitization process, as previously discussed. Hrbacek further state, “The assumption of the existence of inaccessible cardinals requires a ‘leap of faith’ (similar to that required for the acceptance of the Axiom of Infinity)… .”148 However, the similarity is more superficial than it seems, because the acceptance of the axiom of infinity in ZFC requires only the relatively minor conflation of the finite with the infinite with regard to a countable set, as we have already discussed. But the leap of faith required to accept inaccessible cardinals is far greater, because inaccessible cardinals are uncountable, and thus the very concept of infinity that they represent is logically contradictory. But to give a certain “intuitive justification for the plausibility”149 of making this leap of faith to believe in, or to accept, the existence of inaccessible cardinals, Hrbacek discuss “first-order” and “second-order” mathematicians. Those of the first order are mathematicians as we know them, who are able to conceive of “normal” and “intuitively acceptable” infinite sets, such as the naturals or the reals, as “finished” or “completed” totalities, and all sets which first-order mathematicians can conceive of in this way are to be called sets of the first order. But, it is claimed, first-order mathematicians cannot conceive of a set of all sets, because such a set is a logical contradiction, and so such a set would not be a set of the first order. However, a more powerfully gifted mathematician, whose existence we may postulate, who is a mathematician of the second order, can perceive the “set of all sets of the first order” and other so-called second-order sets as completed totalities, and through the usual set-theoretic operations can create and perceive many more sets in addition to these that are also beyond the capabilities of any first-order mathematician to conceive as completed totalities. In such a second-order set universe, a second-order mathematician may intuitively conceive of an uncountable cardinal that is both regular and greater in cardinality than all first-order ordinals, including first-order limit ordinals, and thus this uncountable cardinal that can be conceived as a completed totality by second-order mathematicians satisfies the definition of inaccessible cardinal.150
But there is no logical justification for this argument. The argument is an outgrowth of a desire for inaccessible cardinals, as well as uncountable infinity in general, to exist, not one that is based on sound reasoning. In fact, like the statement of CH itself, in only appears to be based on sound reasoning. First, “first-order” mathematicians can only “conceive” of infinite sets such as the rationals or the reals as “completed” entities because they can conceive of the finite patterns by which the numbers in each set are created, the naturals by the successor function and the reals by combining the rationals with the irrationals one number at a time, the same way the naturals themselves are accumulated. But the reason such sets are intuitively understandable is because each is an accurate representation of infinity (after the necessary correction in our perception of the reals so that we understand that they are countable). With inaccessible cardinals, as with all uncountable numbers, the conception of infinity that these numbers present is logically contradictory, and thus is not understandable by anyone. For the concept “understand” to mean anything at all, the understanding must happen rationally, that is, logically. If an idea contains a logical error, it cannot be understood, period, because it is inherently non-understandable. To postulate a “second-order” mathematician is to grasp at straws, out of a desire to find any way to bolster the emotionally satisfying belief that the uncountably infinite exists. Only the logically valid can be understood, and this “first-order” mathematicians can already do. There is literally nothing beyond this. The idea that there is or could be something beyond this is reinforced by the fact that we have grown accustomed to the idea that there exists both countable and uncountable infinity, and that we intuitively understand countable infinity but can seem to find no way to intuitively understand uncountable infinity. If, for the sake of argument, we say that uncountable infinity exists, and if uncountable infinity is assumed to be a logically valid concept, as it presumably must be if it is based on the “unassailable” and “intuitively clear” diagonal argument, and if its treatment in set theory has been based on quite strict logical definitions, manipulations, and conclusions that have themselves been based on an extension of many logically valid concepts from finite and countable mathematics, then it might seem to make sense that a “second-order” mathematician could exist that could conceive intuitively of the nature of uncountability the way we, at the level of the first-order, can conceive intuitively of countable infinity. Under such assumptions, it is not a stretch then even to say that perhaps someday some of our mathematicians will become second-order after sufficient thought and reflection, since, after all, they do think about mathematics and set theory logically, and uncountable infinity is a logical extension of countable infinity. But once we realize the logical error in the idea that there are different levels of infinity, this kind of hierarchy of mathematical understanding can be seen to be not only entirely implausible, but superfluous. At best, there are different levels of mathematical insight, ingenuity, creativity, drive, and dedication among first-order mathematicians. The concept of a “second-order” mathematician that can somehow go beyond this is nonsensical.
We should note one more thing, and this is in regard to the “set of all sets” being a logically contradictory concept. First, we can see that a set that contains all well-founded sets except for itself is a concept that is easy to understand, because it is nothing but a perpetually growing, i.e., never complete, collection of sets of finite elements, each of which can have its own finite elements within it, but such that a regress within an element always ends at a fixed point, making all such elements ultimately grounded. Such an infinite collection of sets is countable, because we can map the sets within this outermost set one-to-one with the natural numbers. But then imagine that we decide to include this outermost set within itself, as an element of itself. Then we are forced into an infinite regress within this particular element of the outermost set. The same would be the case if we allowed the set to be non-well-founded in general. But we have already discussed this in a previous section. Such infinite regresses are always enumerable, and thus countable, which means that this type of infinity is one which we can “intuitively understand,” and thus accept in the same way that we accept the infinity represented by the natural numbers themselves, albeit after a little demystifying of the nature of infinity and the nature of non-well-founded sets. Therefore, there is no logical contradiction inherent in such a conception, in the sense of the logical contradiction inherent in Russell’s paradox or in the idea of an irresistible force meeting an immovable object. The only logical contradiction relevant for this would be in the assumption that the “set of all sets” could actually be completed, which would be to conflate the finite with the infinite. But this is no different from the logical contradiction that the naturals, or the rationals, or the reals, or the integers, can be considered completed sets. If we have concluded that the latter sets do not contain any logical contradiction in their definitions, then to be consistent we must conclude that the former does not either. The “set of all sets,” then, can indeed be conceived by first-order mathematicians. Notice also that such a set does not include transfinite numbers or uncountable cardinals, because these are not logically valid entities, and so they cannot logically exist, either physically or conceptually, in order to be added as elements to a set. If the “set of all sets” is defined to include the transfinites and uncountables, then, indeed, such a set cannot be conceived by first-order mathematicians; but this is not because of a lack of mental capacity on the part of first-order mathematicians for the “higher” realms of logical thought or existence, but because the concepts themselves of transfinites and uncountables are logically flawed, and so sets that are postulated to contain such numbers are themselves logically flawed conceptions, and thus inherently non-understandable. The same is true of any logical contradiction that we propose to include in the definition of “set” – if there is any logical contradiction at all involved in this definition, such as the idea that a set can have the property of containing all and only the sets that do not contain themselves, then a “set of all sets” cannot be conceived by first-order mathematicians; but this would only be because not all logical contradictions have been expunged from the definition of “set,” not because such a set requires a “second-order” mathematical mind to intuitively conceive.
Hrbacek state that an axiom they discuss which references the cardinal 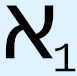 , treated as an inaccessible cardinal, “produces a mild improvement on the results obtained from the Axiom of Constructibility. To get better results we have to assume existence of cardinals much larger than mere inaccessibles.”151 (Italics mine.) They also state that the Axiom of Projective Determinacy has many intuitively appealing and mutually interconsistent results, and because of such thing many theorists in descriptive set theory lean toward the idea that PD is true.152 Once again, if enough logically valid concepts are intermixed with logical errors and flaws, then interesting, “profound,” “deep,” etc., results may be obtained about the logically contradictory ideas. But, again, these are, to one extent or another, red herring results, because they are partly based on logically flawed assumptions. They may, e.g., be based on logically valid arithmetical operations and manipulations, and on the basis of the flawed assumptions may be flawless in their deductions, and because the operations are on transfinite numbers we conclude that something “profound” has been proven when we find a connection to some other result that is also based on the logical error of assuming the existence of transfinite numbers. But to get to the point where what we have concluded in our investigations is or could be a fully accurate account of some aspect of reality, we must eradicate logical errors from our ideas, thoughts, and assumptions completely, instead of partially or mostly. The latter may work in cases where approximations to the truth are acceptable, but they will never work when the perfect or full truth must be known.
, treated as an inaccessible cardinal, “produces a mild improvement on the results obtained from the Axiom of Constructibility. To get better results we have to assume existence of cardinals much larger than mere inaccessibles.”151 (Italics mine.) They also state that the Axiom of Projective Determinacy has many intuitively appealing and mutually interconsistent results, and because of such thing many theorists in descriptive set theory lean toward the idea that PD is true.152 Once again, if enough logically valid concepts are intermixed with logical errors and flaws, then interesting, “profound,” “deep,” etc., results may be obtained about the logically contradictory ideas. But, again, these are, to one extent or another, red herring results, because they are partly based on logically flawed assumptions. They may, e.g., be based on logically valid arithmetical operations and manipulations, and on the basis of the flawed assumptions may be flawless in their deductions, and because the operations are on transfinite numbers we conclude that something “profound” has been proven when we find a connection to some other result that is also based on the logical error of assuming the existence of transfinite numbers. But to get to the point where what we have concluded in our investigations is or could be a fully accurate account of some aspect of reality, we must eradicate logical errors from our ideas, thoughts, and assumptions completely, instead of partially or mostly. The latter may work in cases where approximations to the truth are acceptable, but they will never work when the perfect or full truth must be known.
Potter states, “Since [the 1960s] second-order logic [unlike first-order logic] has been very little studied by mathematicians (although recently there seems to have been renewed interest in it, at least among logicians). So there must have been a powerful reason driving mathematics to first-order formulations. What was it? We have already noted the apparent failure of attempts to supply plausible constraints on inference which characterize first-order logic uniquely, but if first- and second-order logic are the only choices under consideration, then the question evidently becomes somewhat simpler, since all we need do is to find a single constraint which the one satisfies but not the other. Yet even when the question is simplified in this manner, it is surprisingly hard to say for sure what motivated mathematicians to choose first-order over second-order logic, as the texts one might expect to give reasons for the choice say almost nothing about it… . Goldfarb (1979) illuminates the context for the rise to dominance of first-order logic, without really attempting an explanation for it. Some further clues are offered by G. H. Moore (1980). However, there is much about this matter that remains obscure.”153 We will not consider the specific personalities and historical details involved in this rise to dominance. We will only say here that given the logical error at the root of Cantor’s diagonal argument and at the root of the theory of uncountable infinity in set theory, and given mathematicians’ overriding interest in logically valid results, it is not especially surprising that mathematicians have generally restricted their work to the kind that can be understood by means of first-order logic, since first-order logic contains an accurate representation of the nature of infinity, viz., that it is countable only. This is the distinguishing factor or “constraint” that represents the essential difference between first- and second-order logic which can account for the specified trend among mathematicians. Higher-order logics, as well as certain “extensions” of first-order logic, allow for the ideas of uncountable sets and uncountable infinity to creep into the formalisms: “… many extensions of first order logic have a Completeness Theorem, most notably the extension of first order logic by the generalized quantifier ‘There are uncountably many’ and the infinitary language Lω1ω … . second-order logic is—almost by definition—able to say that a set is the power set of another set. What this means is [that] the models [of second-order logic] are necessarily uncountable. This shows that second-order logic, unlike first order logic, has sentences with models but only uncountable ones… . Second-order logic hides in its semantics some of the most difficult problems of set theory.”154 Difficulty in clearly understanding the nature and mathematical significance of second- and higher-order logic comes from the flawed assumption that Cantor’s diagonal argument and the theory of uncountable infinity in set theory are logically valid. Of course, if one believes this, it will be more difficult to understand the changes and trends that have happened in broader mathematics in its use, either directly or indirectly, of the ideas from mathematical logic. This, in fact, is another example of a logical error in our assumptions creating intellectual opaqueness and roadblocks which stand in the way of our coming to a clear understanding and our being able to answer a question; and, in fact, the logical error at the root of this murkiness is the same one that is at the root of the murkiness of CH and Suslin’s Problem, viz., the conflation of the finite with the infinite and the assumption that there are different levels of infinity.
Potter states, “[The theory of cardinals and ordinals] is hardly controversial nowadays: it may still be a matter of controversy in some quarters whether infinite sets exist, but hardly anyone now tries to argue that their existence is, as a matter of pure logic, contradictory. This has not always been so, however, and the fact that it is so now is a consequence of the widespread acceptance of Cantor’s theories, which exhibited the contradictions others had claimed to derive from the supposition of infinite sets as confusions resulting from the failure to mark the necessary distinctions with sufficient clarity.”155 Potter makes the same comments that are made in this paper regarding set theory’s use “as a tool in understanding the infinite” and in “taming the infinite.”156 But here Potter also falls into the trap of not understanding that Cantor’s theory of cardinals and ordinals is based on a logical flaw, the conflation of the finite with the infinite. We have already shown in the previous part the precise nature of the flaw in Cantor’s famous diagonal argument. Potter states that Cantor showed that the criticisms of the concept of completed infinity were based on confusions, and implies that Cantor’s theory can be seen to be logically valid and clear if we take sufficient care to ensure our concepts are clarified. And yet Cantor was never able to make any significant progress in resolving the continuum hypothesis, and neither has anyone else prior to the present paper. Should we wonder why? Or should we consider that Cantor’s theory of the infinite was not as clear and precise as he thought it was? On the basis of the understanding of the infinite presented in this paper, we must choose the latter. We will not discuss whether Cantor was correct in his claim or belief that the criticisms raised against the concept of completed infinity, or even directly against his theory of the infinite, were based on confusions; in fact, they all might have been, and Cantor might have been correct in every instance in which he rejected such a criticism as invalid. A criticism raised against an invalid idea or theory may itself be invalid, either in whole or in part; but this does not mean that the invalid idea or theory being criticized is or must be valid itself. If someone proposes a theory, and all criticisms raised against it at the time of its proposal, and perhaps for 5, 10, 15, etc., years afterward, are shown to be invalid, then if there is not an inherent reason in the theory itself to logically accept the theory as correct, we must take what is commonly understood to be the “scientific” approach, and say that thus far the theory has stood the test of time, and so we may begin to feel reasonably confident that the theory is correct. The implication here is that, of course, we do not know that the theory is correct, so there is always the nagging doubt that this lack of complete certainty can from time to time produce in our minds, the doubt that perhaps, just perhaps, something about the theory is flawed, and we are simply at a loss, at least at the present time, as to what this flaw might be. But the thing is, in the realm of the logically necessary, such as that studied in mathematical logic, metamathematics, philosophy, and set theory and its foundations, we can do better than the mere “provisional” nature of the results of the typical scientific investigation or enterprise, because we ourselves can perceive logical necessity. In typical scientific investigations, on the other hand, there is always the possibility that we have not gathered the necessary data in order to perceive some facet of what we are studying. In the realm of logical necessity, we may make definitive arguments. The only requirement is, as Potter states, that our concepts are sufficiently clarified and logically valid.
With regard to the fact that hardly anybody today in mathematics (or philosophy or set theory) would argue that it is an actual logical contradiction for an infinite set to exist, we have already discussed this in earlier sections. If the process which produces the elements in the infinite set is finite, i.e., if it is a pattern, we can clearly see how it can be applied any number of times in a countable way, and thus it is intuitively understandable how such an infinite sequence of elements can be produced. This, in turn, is because countable sets are accurate representations of the nature of infinity, and as such are logically comprehensible. It is not surprising, then, that after many years and decades of thinking about this type of mathematical operation, it has come to be the case that the vast majority of practitioners accept that such sets exist. But if we just leave it at this, we will not see the more subtle flaw in this reasoning, and will thus not be able to, for example, find the correct way to resolve CH. Yes, in various mathematical circumstances it is a good approximation to the full truth to say that the finite pattern that produces this infinite sequence of elements is equal to the infinite sequence itself, or, in any case, to implicitly and subconsciously assume this to be so; but it is incorrect to say that the two actually equal each other. In the process of growing as accustomed as we have to equating the two, we have made ever more remote the recognition of the logical error in doing so, and have made it that much harder for us to resolve CH, Suslin’s Problem, and other problems that bear directly on the nature of the relation between the different supposed levels of infinity. In our desire to find the ultimate nature of reality and logic, and be absolutely certain about things, we have performed the necessary mental gymnastics to get two things, one finite and one infinite, to resemble each other as closely as we can, and have been satisfied with equating the two based on this resemblance, and then for the most part not thinking further about it, except for the purpose of trying to find additional, preferably mathematical, ways to feel even more justified and validated in this equating. Such a feeling allows us to have a measure of that sense of certainty which we so desperately crave, and this satisfactory feeling itself makes it that much harder to recognize the logical error involved. There is a logical contradiction in the idea that an infinite sequence of elements can be comprehended as a finite, completed, finished thing. But because the nature of countable infinity is logically valid, we can easily understand how it is possible to treat such infinite sets “as a whole” for various mathematical and logical manipulations. But if we look more closely at these manipulations and treatments, we find that we are only ever treating each element in such an infinite sequence of elements individually in any concrete task or operation, and we only think of the infinite sequence itself “as a whole” or “as a completed thing” because it is convenient to do so in our thoughts and discussions about these infinite sequences, not because doing so is logically valid. Moreover, it is convenient to think of such an infinite sequence in this way precisely because we can comprehend as a finite thing the specific pattern, or algorithm, used to generate each new element in the sequence, and as such it becomes that much easier to treat the infinite sequence itself as if it were the finite pattern which generates it. We should note that both Potter and Hrbacek make the same comment about infinite sets, viz., that the key reason we should accept the existence of infinite sets comes down to the fact that the vast majority of researchers in the relevant fields accept their existence. But we notice that this falls short of being a logically necessary or definitive reason to accept their existence. The authors desire that the issue be settled, rather than remain open, and so they make the strongest argument they can for why it should be settled; but the argument fails to settle the issue, because it relies on shared acceptance of an idea, which is prone to error, rather than on logical definitiveness or necessity, which, as we have stated, is possible in this realm of inquiry, once all relevant concepts are sufficiently clarified.
Potter makes insightful comments about set theory and about the meta elements of set theory. But he, like most set theorists, places too much faith in the supposed unassailability of the diagonal argument, and the theory of different levels of infinity which is its natural consequence. In fact, the diagonal argument is based on a logical error, and thus its conclusion about infinity is incorrect. Cantor, in other words, did not think as clearly about the nature of infinity as many practitioners of set theory and its philosophy wish to believe.
Potter states, “… if there is a set-theoretic paradox that is not analysable in terms of indefinite extensibility, then by the nature of the case it involves a wholly new idea, and we plainly have little idea in advance how likely this is to occur.”157 However, as we have discussed, the only logically valid type of infinity is countable infinity, and, as such, any set-theoretic concepts which restrict themselves to that which is logically valid are by their nature either finite or “indefinitely extensible.” Any paradox with regard to the infinite that cannot be analyzed in terms of indefinite extensibility is one which contains within it a logical error and thus is not able to be resolved in any way other than by recognizing and eliminating the logical error. Indefinite extensibility is, as discussed, the process by which a finite algorithm, i.e., a pattern, is able to produce an infinite sequence of elements, and in the context solely of this logically valid understanding of infinity, i.e., of countable infinity not marred by the intermixing of the ideas of uncountable or finitized infinity, it is impossible to have or to deduce an actual paradox.
In discussing axioms of infinity in relation to the different levels in his hierarchy of sets, Potter states, “It is not hard to persuade oneself that there is no limit to the strength … of the axioms of infinity that can be devised. What will interest us in this chapter is rather whether there is a limit to the strength of axioms of infinity that are true, and, if so, what it is.”158 Each axiom of infinity is thought to correspond roughly to a particular level in the hierarchy, so that a stronger axiom of infinity, postulating a larger cardinal, is to be found only at a higher level in the hierarchy.159 But we have already discussed at length that the only possible level is the one that models the finite and the countably infinite. Any higher level, i.e., any level that introduces the concept of the uncountably infinite, introduces a logical error in the theory and thus cannot possibly introduce a truth. In other words, there is a limit to the strength of axioms of infinity that are true, and this limit is precisely at the point where the theory encompasses countable infinity, and, in particular, only in a way that does not include the implicit or explicit claim that completed infinity exists or can exist.
Gödel’s second incompleteness theorem says that there is a statement within any sufficiently powerful formal axiomatic system which says that the system itself is consistent but which is unprovable within the context of the system. Potter discusses this and says that these statements “can also, like any arithmetical sequence, be interpreted set-theoretically as saying something about ω.”160 He then states that if a particular set theory is strictly stronger than the set theory in question, then it is reasonable to assume that the stronger set theory, which is based on a stronger axiom of infinity, can be used to prove the validity of the consistency statement of the weaker set theory. He goes on: “… what is significant is that it is an elementary arithmetical [claim]; i.e., it is obtained from a sentence in the first-order language of arithmetic simply by interpreting the quantifiers in that sentence as ranging over ω.”161 But it is not surprising that we can recognize that the consistency statement is true, since all it is is a statement that, as Potter says, ranges over the set of natural numbers; in other words, we can clearly see the pattern that produces the natural numbers as part of the consistency statement, but because first-order logic can only operate at any given time on a single number, a single finite individual, it is not powerful enough to make general statements about the entirety of a countably infinite collection of individuals. But the conclusion that we must involve the uncountably infinite, via the addition of a stronger axiom of infinity in second-order logic, to formally prove the consistency statement, is mistaken, and this conclusion is the conceptual result of the logical error of equating the finite with the infinite, specifically the finite pattern that produces the natural numbers with the infinite sequence so produced. We think of the infinite sequence of natural numbers as a linear, never-ending sequence, but at the same time we have subconsciously equated this infinite sequence with the finite pattern that produces it, and we then subconsciously conclude that because the pattern itself is finite, then the infinite sequence must be able to be finitized. We then conclude erroneously that it is necessary to add a stronger axiom of infinity and introduce a higher-order logic system that includes it so that we can treat the entirety of the natural numbers, ω, as a completed or finished totality, which then allows us to prove finite statements in mathematical logic about this totality. But what we have done here is, in stepping outside the finite pattern that produces the natural numbers we believe that we have been able also to “step outside of,” or more correctly, to “step beyond,” the infinite sequence of natural numbers itself, which then gives us a sense of justification in believing that it is possible to propagate the number sequence beyond the end of the natural numbers, when it is not. Note that there can be a level of convenience in thinking this way, and we can recognize that to this extent such a conception can be helpful in making explicit the implicit truths that we can see but not prove in the context of first-order logic. But it is not logically valid to take things beyond this point. In other words, if we start to think of the stronger axiom of infinity as representing an actual number, an actual totality, that is beyond the totality of the natural numbers, then we have ventured into the realm of logical error. It is only the idiosyncrasies of how first-order logic is defined and restricted that prevent the first-order system from proving the truth of the consistency statement. But it is not necessary to invoke stronger axioms of infinity and uncountable cardinals to prove the truth of the consistency statement. It is simply necessary to modify first-order logic so that it is able to encode, in a formal way, the notion of pattern. By doing this, we do not use the logically flawed conception of uncountable infinity, with the permanent opaqueness and intractability which this conception brings; instead, we not only provide a useful extension to so-called first-order logic, but also bring to greater prominence the fact that there is nothing higher or bigger than countable infinity, and that, unlike with the useful approximations in various mathematical contexts, in a formal system of logical truth the finite should never be equated with the infinite.
In discussing the limitation of the hierarchy of levels defined so far in his book regarding the fact that the levels do not extend to include level Vω+ω, Potter suggests adding the “axiom of ordinals,” which says that every ordinal has a level in the hierarchy which corresponds to it, to the list of axioms of his set theory. This then allows for the level Vω+ω to exist, as well as a level for every higher ordinal. However, he then discusses the very limited applicability for this axiom thus far in broader mathematics, and the fact that the “overwhelming majority”162 of broader mathematics barely breaches the level of ω itself, and thus remains entirely within the realm of the countable. As a result of this, he states, “the principle argument for [the validity of the axiom of ordinals] must [therefore] be intuitive. The most obvious such argument is that there is no good reason why the hierarchy should not extend beyond Vω+ω, and so by some version of the second principle of plenitude, we conclude that it does so extend.”163 The second principle of plenitude is discussed by Potter in the same book on pp. 55-56; he does not define it precisely, and indeed discussed the difficulty of precisely defining it. But it is basically the idea that there exist as many levels in the set/collection hierarchy as it is possible for there to be. As Potter states, this is not a precise definition, but it is sufficient for our discussion here. However, Potter’s argument conflates the finite with the infinite. The only reason he thinks that there is no good reason why the hierarchy should not extend to ever-greater ordinals at ever-higher levels is that he is already comfortable with treating the transfinite ordinals, which are examples of finitized infinity, as if they were actually finite things that could be lined up in order of magnitude, and then more or less subconsciously superimposes the countable infinity of the natural numbers onto this sequence of transfinite ordinals; also, since the concept of infinite sequences of uncountable ordinals is already a mainstay in set theory, Potter has a strong motivation to ensure that his theory of levels encompasses it, in order that his theory of levels accurately represent what the vast majority of set theorists say is the truth about sets. But once the specified superimposition is done, we find it impossible to imagine that the sequence of transfinite ordinals could ever end; however, this is precisely because the sequence of natural numbers never ends. When we have, over time, altered and molded the ideas and half-ideas in our minds so that they come out in the particular illogical shape we want, in this case the shape that allows us to view infinity as a finite thing, then in the context of this particular cast of ideas we will have trouble understanding why certain things which seem like they should be possible, and thus logical, seem at the same time to have deeper flaws or whose conceptions seem to be particularly foggy or nontransparent, and we will also not be able to see why certain things that we think should be possible or are possible are actually not possible. It is, in fact, not possible to extend the hierarchy in the way Potter describes, because there is no such thing as uncountable infinity (which would be included in the list of all ordinals), and because, as Potter himself indirectly implies, the number of levels themselves can always only be finite, and we may increase them as high as we like only in the context of countable infinity, the “end” of which can never be reached. Also, if the first level already represents countable infinity, then there can only ever be one level, nothing more. A better, though still not as precise as we could make it, version of the second principle of plenitude, then, would be that if no particular level ever entirely encompasses countable infinity in its definition, then we can create as many levels as we like, but the total number of these levels at any given time will always be finite, and it will be literally impossible to produce all of these levels as a completed collection of levels; or, if the first level represents countable infinity already, then there can be literally nothing beyond the first level. In the first case, we may for convenience envision these levels in their entirety in the same manner we do for the naturals, the rationals, etc., viz., by conceiving of the pattern that produces them, but if we do this, we must keep in mind the difference between the pattern that produces an infinite sequence and the infinite sequence produced by the pattern. In the second case, we have, effectively, made use of this exact convenience.
We may make another note here. In discussing the second principle of plenitude, Potter states, “When we come to express the second principle … we might do so by saying that all the levels exist that are possible where the type of possibility invoked might now be narrower (e.g., metaphysical or conceptual possibility). There is difficulty at this point, of course… . To say that there are as many levels as possible seems contradictory, because however many there are, there could have been more: just take the union of all of them. If we simply deny that there is such a union, we are left struggling to explain why not… . [T]he platonist conceives of the universe as static. There are just the sets there are… . And yet it seems to be the essence of the conception that the second principle of plenitude urges on us to keep on trying to destabilize this static picture.”164 But the seeming contradictory nature of this proposal for the total number of levels that could exist, the seeming urge to keep trying to destabilize the static platonist picture, is actually a sign, however obscured and buried, of the true nature of infinity, viz., that no countably infinite sequence can ever end. By making the clear statement that simply requires that all levels exist that are possible, we come to face more squarely and more obviously the infinite nature of countable infinity, albeit disguised as an infinite sequence of levels each representing a higher level of infinity than the level below it. What Potter struggles with here is the reality that it is logically contradictory to equate the finite with the infinite, i.e., that in “specifying” a particular “amount” as the “most” there ever could be in terms of levels, one has specified, albeit indirectly, a finite, fixed quantity, and as soon as we specify a finite, fixed quantity, we can perceive how to step outside of or beyond it. What Potter encounters here in fractured and incomplete form is the true nature of countable infinity, mostly hidden from view submerged in the cold water and beating on the ice from underneath, trying to break through to the surface. We only need acknowledge that the sole logically valid type of infinity is countable infinity, and the entire problem of the height of the hierarchy goes away, because when there is only countable infinity the reality is that there is no need for a hierarchy anymore, since no hierarchy is necessary to complete the description of all possible sets.
Potter states, “Non-self-membership was not the first instance of a non-collectivizing property to be discovered: Cantor told Hilbert in 1897 that ‘the set of all alephs … cannot be interpreted as a definite, well-defined finished set’… . Hilbert referred in his (1900) lecture on the problems of mathematics to ‘the system of all cardinal numbers or even of all Cantor’s alephs, for which, as may be shown, a consistent system of axioms cannot be set up’.”165 And why exactly would Cantor and Hilbert draw these conclusions? But based on the content of the present paper, we may say that it is quite clear why Cantor had difficulty visualizing the “set” of all alephs as a definite, well-defined, and finished entity: alephs are not numbers, but concretizations of infinity, and as such are themselves logical contradictions; therefore, of course Cantor had, and anyone else will have, a certain nagging difficulty conceiving of them being placed as elements into a set, much less conceiving of a completed collection of an infinite, and even more, an uncountably infinite, number of these entities. No matter how hard he tried, Cantor was simply not able to figure out how to make such conceptions logically meaningful, and thus intuitively satisfactory. But this is inevitable with logically flawed ideas. And why, as Hilbert claims, should it be the case that it can be “shown” that such a collection cannot have a consistent system of axioms set up for it? Well, of course, this is because the concepts on which such a collection is based are logically flawed. When one tries to find a logically valid way to express the meaning and nature of logically flawed ideas, one will inevitably encounter impossibilities and permanent roadblocks such as these, as well as murkiness with regard to why one has run into such impossibilities and roadblocks. Only when one corrects the logical error in one’s thinking does the murkiness clear up and all become understandable again. These “definitive” statements by these idolized mathematicians, then, do not provide the kind of “definitiveness” that we are usually meant to draw from them, and that their originators presumably meant us to draw from them – they do not provide justified reinforcement for the conclusion that such sets of alephs are logically valid concepts that simply cannot be interpreted or understood according to our current methods or level of understanding; rather, they serve to subtly emphasize, without our, or their originators’, necessarily realizing it, the expression and reticulation of a logical error through our reasoning, like gristle in meat. In order to realize the true significance of these difficulties, we must “mark the necessary distinctions with sufficient clarity.” Only after we have done this can we say that we have drawn a logically valid conclusion. Potter goes on to say, “What is particularly striking about Russell’s paradox, however, is that it is in essence more purely logical than the others… . By contrast, the other set-theoretic paradoxes involve cardinal or ordinal numbers in some way. Curiously, Hilbert described these other paradoxes (in a letter to Frege) as ‘even more convincing’: it is not clear why.”166 Russell’s paradox can be considered more “purely logical” because, like the irresistible force meeting the immovable object, the contradiction involved is solely contained in the defining arrangement of things being considered; i.e., the components being considered in the statement of the paradox are themselves individually logically valid, clearly understandable concepts or things, and it is simply that they are being placed into a logically contradictory arrangement. The paradoxes of the sets of alephs, cardinals, ordinals, the sets of their sets, etc., on the other hand, are about entities or things which themselves are logically contradictory, on top of the fact that they are sometimes, as in the case of uncountable such sets, or countable such sets that are treated as finitized infinities, placed into logically contradictory arrangements. This is the key difference, and this disparity results in a difference which can be perceived with regard to the nature of the “paradox” in these things, as opposed to that in, e.g., Russell’s paradox. The confusion regarding such things on the part of Cantor, Hilbert, Potter, and many others, stems from the fact that the logically contradictory concepts or entities used as objects in the latter type of paradox – the alephs, cardinals, etc. – as well as the logically contradictory arrangements in which they are sometimes placed, are treated and thought of as logically valid.
As for why Hilbert described the paradoxes regarding the alephs, etc., as even more convincing than a “typical” paradox like Russell’s paradox, it would be helpful to know more of the context of Hilbert’s personality, life, and thoughts. However, even without these things we can still say that to the extent that Hilbert believed in the logical validity of the concept of finitized infinities, their ability to be meaningfully mathematically manipulated, etc., he was still in the essential grip of the crude but powerful evolutionarily-built fear of death, i.e., he had not conquered this fear in the most essential ways, and so he was still subject to the built-in psychological and emotional protection which blocks recognition of the essential logical error in such ideas, which recognition would cause the theory of the uncountably infinite and of finitized infinities to completely crumble and dissipate. Within the context of such a mindset, one which sees the uncountably infinite as a pathway to the actual conquering of infinity, and thus, in a crude but powerful emotional way, to the overcoming of mortality, paradoxes with regard to the “uncountably infinite” can seem like “even more profound” paradoxes, or “truer” paradoxes, than the comparatively simple, drab, boring, lackluster, mundane, uninspiring, trite (etc., etc.), easily understandable paradoxes like Russell’s paradox, because paradoxes of the former kind will have a stronger emotional pull, due to the sense of their greater potential for helping overcome mortality, on a psyche which has not conquered death in the essential ways.
Further, Potter states, as a proposition, “The set of all cardinals does not exist.” For the proof, he says, “If there were a set of all cardinals, it would have a largest element … contradicting [the fact that Cantor’s theorem that every set is smaller in cardinality than its power set implies an infinite sequence of ever-greater cardinals].”167 In other words, if the set had a greatest element, we could easily see how to go beyond this greatest element, contradicting the initial assumption that it is the greatest element, i.e., the set would be shown to be finite, contradicting the initial assumption that it is infinite. But note that this is the exact argument that we have used in the present paper to point out the fact that the natural numbers cannot exist as a set, i.e., as a completed thing with a fixed number of elements. It is simply that in the context in which infinite cardinal numbers are the elements of the set in question, this realization is, in modern set theory, easier to arrive at. Why is it easier to acknowledge that an infinite list of infinite quantities cannot be collected together into a finite thing than it is to acknowledge the same thing for an infinite list of finite quantities? But the answer already presents itself. There is less at stake for set theorists in the former acknowledgment, because there is in this no danger of destroying any essential portion of their theory of the transfinite. But if they were to acknowledge the latter, they would be forced to also conclude that it is logically contradictory to go beyond the countably infinite, which, in turn, would mean they would have to acknowledge the logical error in the entirety of the theory of the transfinite and uncountable infinity, and, in particular, in the diagonal argument. We may also say that since the concept of an infinite cardinal being a finite element of a set already contains a contradiction in it, there is some fuzziness, i.e., murkiness or opaqueness, in the idea of collecting an infinite number of them together which does not exist in the idea of collecting an infinite number of actually finite entities or quantities together, and this, indirectly, adds an additional level of uncertainty on the part of set theorists regarding the nature of such an infinite collection, or what can be said about it. Potter, in fact, very indirectly acknowledges the problem, when, in a footnote about cardinal numbers, he says, “If there happens to be infinitely many individuals, finite cardinals will in fact be infinite sets.”168
Potter makes the comment that “any system of notations is countable and will therefore fail to exhaust ω1.”169 Recall that ω1 is the first uncountable ordinal. Of course, it is clear that in any system of notations each notational symbol is a fixed, finite thing, a particular symbol that is made to represent a single ordinal, starting with 0 and continuing into the transfinite with ω, then the symbol that represents ω+1, etc. If ω1 is supposed to be uncountable, and thus beyond the “end” of the countable numbers, then, of course, a countable set of symbols can never actually reach the ω1 point in the sequence of numbers. But what is not realized here is that no system of notations can exhaust the natural numbers, i.e., a countable system of symbols can never complete assignment to a countable set of numbers. A countably infinite list of elements can never end, because it is, by definition, infinite, and so not only can one never reach ω1 with a countably infinite sequence of symbols, it is impossible even to reach the “end” of the natural numbers with such a sequence of symbols; in fact, a part of why it seems so hard to create a completed system of notations for the ordinals leading up to ω1, aside from the fact that the concept of uncountability is logically nonsensical, is precisely that we feel the need to count, that is, enumerate, not only the finite ordinals but also all the transfinite ordinals, as part of our effort to get a handle on their nature. It may be objected that the reason a countably infinite sequence of symbols cannot reach ω1 is precisely because ω1 is uncountably infinite; but this is to fall into the same trap that causes all these paradoxical problems to begin with, viz., the belief that the uncountably infinite and the transfinite in general exist. One cannot “reach” the uncountably infinite, symbolized here by ω1, by a countably infinite sequence of steps, because the countably infinite sequence of steps never ends, and so there can be nothing “beyond” it to reach. The disconnect that Potter discusses between a countably infinite sequence of notational symbols on the one hand, and ω1 on the other, is not that something “more” is needed than a countable number of symbols to “reach” ω1, but that ω1 as a representative of uncountable infinity is a logically contradictory concept, and so it is not surprising that we draw a blank when we try to find an intuitive or reasonable or understandable way to connect the countably infinite with ω1. This is the same rock upon which CH founders.
One other way to look at the set of all alephs is to make an analogy with the set of natural numbers. Potter tells us, “The alephs do not form a set,” and as proof of this statement we are told, “By Hartog’s theorem … there is no cardinal which is an upper bound for the alephs: it follows that they do not form a set … .”170 But why, then, do the natural numbers form a set? There is no upper bound for them either. We only say there is an upper bound, which we call ω, based on the flawed conclusion of the diagonal argument that there are more reals than naturals. But if the natural numbers never end, and yet we have simply, and contradictorily, decided that there is an upper bound to them and decided to use the finite symbol ω to represent this fixed, i.e., finite, upper bound, then by the same logic, and with the same degree of justification, we can arbitrarily decide to say that the sequence of infinite cardinals also has a fixed upper bound, which, say, we will call Ϡ. Aside from the fact that infinite cardinals are not fixed, finite quantities themselves, and so it makes no sense to say that they can be ordered in a sequence by their magnitudes, the legitimacy of this conclusion is no less than that of the conclusion that the natural numbers are bounded on their upper end by ω. In other words, both conclusions are absurd and logically flawed. This is implicitly acknowledged by set theorists’ recognition that the sequence of infinite cardinals, when these cardinals are treated as finite entities arranged by magnitude, does not have an upper bound. They are just not consistent enough, and brave enough, to apply this same conclusion to the natural numbers.
Potter gives a definition of the concept of “supertask” by saying that such tasks are “tasks which can be performed an infinite number of times in a finite period by the device of speeding up progressively (so that successive performances might take 1 second, ½ second, ¼ second, etc., and the supertask would be complete in 2 seconds). But there seems to be little hope of extending this idea to the uncountable case… . What we need in general is a method for comprehending infinite collections by means of something that is finite and hence capable of being grasped by a finite mind, namely the property which the members of the collection satisfy.”171 Here “property” is the same thing as what in the present paper we have called the “pattern” or “finite pattern” that generates an infinite set. It should be made clear, though, that a “supertask” is not something that can actually be performed to completion – otherwise it would simply be a task, and would be finite. Treating a supertask as being able to complete by analogizing it with an infinite series of numbers that has a finite limit point as its “sum” is an example of conflating the finite with the infinite, and it is, thus, a logical error to do so. However, as with equating the finite pattern, or “property,” that produces the natural numbers with the infinite sequence so produced, or an infinite decimal expansion with its finite limit point, this equating is a readily understandable conflation of the finite with the infinite, because it deals strictly with countable infinity, and so useful practical applications of this conflation, where we are satisfied with approximations to the full truth, can be made of it. But we must always remember that the idea of a supertask is a practical conceptual convenience; a supertask is not something that can actually exist or happen; infinity is infinite, and thus a supertask is never complete. Another way of saying this is that a supertask would at “completion” perform the final task in 0 seconds, i.e., it would be able to perform a task in literally no time at all; but this is a logical contradiction, because any task, no matter how fast it is done, is always performed in a non-zero amount of time. It can be easy to map or analogize this concept to that of an infinite series with a finite limit point which represents the “sum” of the series as a way to feel as justified as possible in believing that in concluding that a supertask can complete we are making no logical error, since we are already mathematically comfortable with such sums; but we will do well, for the purpose of understanding reality’s foundations, to remember that such conflation is a practical conceptual tool only. As for Potter’s comment about how there seems to be little hope of extending the conception of a supertask to the uncountably infinite, well, this is not surprising, since the concept of the uncountably infinite is logically contradictory, whereas the concept of the countably infinite is not; the attempt to extend the concept of supertask from the countable to the uncountable is the same as the attempt in CH to relate countable infinity to uncountable infinity, and it is just as meaningless and just as impossible. We should also note that, though in certain ways our minds are “finite,” we must not allow this to let us conclude that there is or could be such a thing as an “infinite” mind beyond ours that can understand the “higher” levels of infinity and reality that we cannot. There is nothing but logical necessity and countable infinity, and this the human mind is already capable of understanding. To think that there is anything beyond this is to fall prey to the same emotional motivations and impulses that make acolytes believe in God, which are ultimately expressions of the desire to find something about the world that is eternal, which can then give hope that maybe, just maybe, we might also be made eternal, i.e., might be able to conquer death, if we do or say or think or know the right things. Such desire is couched in more mathematical terms in set theory’s study of the infinite than is the typical statement of belief made by a religious acolyte, and thus in certain ways is expressed in a more logical fashion; but the underlying emotional impulse to conquer death is the same founding motivation for both. Potter makes the further acknowledgment, “Even if the idea of an infinite set is unproblematic, it certainly does not follow that the idea of an infinite thinking being is.”172 Right. If we define an “infinite thinking being” as a being that can comprehend levels or types of logic or infinity that are fundamentally or constitutively beyond the human mind’s capacity, then of course the idea of such a being is problematic, since we are now discussing a being who “comprehends” logical contradictions. But this is literally impossible – not just impossible for the human mind, but for any mind. A logical contradiction is, by its nature, non-comprehensible. Only ideas which are logically valid are comprehensible, and, again, the human mind already has this covered. Also, the very idea itself of an “infinite mind” is logically contradictory, because it posits a completed infinity, viz., a mind that is itself whole or complete but that at the same time is infinite; such a conception, as we have discussed, is inherently nonsensical. Potter also states, “… but it remains to this day a real philosophical perplexity to say how we finite beings achieve this feat of comprehending the infinite (or, indeed, whether we fully do so).”173 Why should this be perplexing, though? But the reason it is perplexing is that the philosophers do not see the underlying principles and patterns of their subject matter clearly and completely enough to fully understand it, which lack of clarity results in definitions of concepts and words that are ambiguous, vague, logically flawed, not representative of the inherent structure of that which is being studied, or mutually contradictory. The word “comprehend” is a good example. If by “comprehend” we mean “completely circumscribe, bound, complete, finish, etc., a collection,” then, by definition, we can never comprehend infinity, which, by definition, is that which can never be circumscribed, bounded, etc. But if by “comprehend” we mean “understand the finite pattern that produces an infinite sequence,” then we do comprehend the infinite. And the reason we care so much about this in the first place is that there is a crude but powerful emotion impulse within us which makes us greatly desire to conquer death, i.e., to conquer transientness, insignificance, weakness – in other words, finiteness. In fact, our emotional desire to conquer finiteness makes it considerably harder to see foundational things clearly, because to see foundational things clearly means to more directly face the inevitability of our own mortality; thus, the mind heavily protects itself, and is evolutionarily built to heavily protect itself, against such deeply troubling knowledge. Once we clarify the concepts, we realize that it is no “feat” for “finite” beings such as ourselves to “comprehend” the infinite – our ability to do so simply reflects the connection between infinite and pattern, and in no way means that we have finitized the infinite itself, which flawed and confusing idea is implicit in the questions we ask about how or whether the human mind could possibly understand the infinite. Of course, by the definition of “infinite,” it is impossible not just for humans but for any thinking entity whatsoever, indeed, for anything at all, to finitize the infinite. But in our understanding of the infinite, we have not, in fact, actually done this, nor is there a need to in order to obtain this understanding.
In a discussion of well-ordered sets, Potter states, “When we discussed the constructivist understanding of the process of set formation, we noted the difficulty that this conception would apparently limit us to finite sets. In order to liberate the constructivist from this limitation, we examined the possibility of appealing to supertasks … . [However,] this method has a limit. This is because the tasks performed in a supertask are well-ordered in time. As a result, if we assume that the ordering of time is correctly modeled as a continuum, we can conclude that any supertask contains only countably many subtasks.”174 This is no different from saying that any countably infinite subset of the real line is null, or that the measure of a countable set is 0. As soon as we are able to clearly see that the infinity we are dealing with is countable, such as is the case with the clearly enumerable tasks of a supertask, then we perceive a seemingly unbridgeable disconnect or gap between the infinity that we are working with and the uncountable infinity that supposedly lies beyond this. The full nature of time must be left for future discussion, but we may still make certain comments here. Time being modeled as a continuum is no different from space, specifically Euclidean measures such as distance, being modeled as a continuum, and we have discussed the irreconcilability of these ideas at length in earlier sections. Time, just like space, being modeled as a continuum, i.e., as an infinite, linear collection of zero-length (or, equivalently, zero-duration) points that somehow can be accumulated together to produce a non-zero, positive measure is, at best, a useful approximation to the truth, and can never be the truth itself. As we have discussed, “uncountable infinity” is a logically flawed, and thus meaningless, concept, and, therefore, neither time nor space can be accurately represented as an uncountable sequence or set of points or elements. In fact, though this takes us a bit afield, the entire concept of using the reductionistic mindset to “break down” time, or space, into its individual parts, so that we may see the inner workings of this aspect of our universe more closely, in order to finally understand it, is simply the wrong approach to understanding time and space. The reductionistic mindset itself is a useful practical conceptual tool, which, like all such tools, has its bounds of applicability; beyond these bounds, it starts to produce nonsensical results, such as the idea that time, or space, can be understood by breaking it apart into smaller, simpler, or more primitive components that can then be understood individually and pieced back together into the whole. The reason a supertask could not solve the constructivist’s problem of how to construct uncountably infinite sets, “given” that there are many sets, e.g., ℝ, that are clearly sets but are also uncountable, is not that a supertask can only perform a countably infinite number of subtasks in a finite time, which would never be enough to perform an uncountably infinite number of subtasks in a finite time (so as to “complete” an uncountably infinite supertask); it is because there is no such thing as “uncountability,” and so this problem is, in fact, not a problem at all, not only for the constructivist, but for everyone and anyone, of any valid philosophical persuasion. Note that even here we are assuming that the supertask of countably many subtasks is able to complete. In fact, because the supertask is defined to contain an infinite number of subtasks, it can never complete; the idea that it can complete, and thus that it can complete in a finite time, is an artifact of the conflation of the finite with the infinite, viz., the treating of an infinite, ever-changing sequence of magnitudes as if it were equal to its fixed, finite limit point. Just because an infinite sequence of numbers approaches a finite limit point does not mean it will ever reach the limit point. In fact, this is impossible. In the case of an infinite series, just because we can see the pattern that its terms conform to, and thus can see the finite value that this series of terms approaches, does not mean that the infinite sum can ever be completed.
How many sets are there? What is the totality of all sets? Is this a meaningful conception? But if we clarify our understanding of infinity, then since there can be an infinite number of sets, based on the infinite number of numbers or things that can be in sets, the totality of sets is countable, i.e., it is infinite and therefore never complete. The attempt to envision the “universe” of sets is another example of the attempt to finitize the infinite, no different from treating the naturals, the reals, etc., as a “completed” collection or thing, and no less subject to the same logical error as these. Because of the way “set” is defined, the universe of sets is countably infinite, and therefore cannot ever exist as a totality. But because we can conceive of the finite pattern by which sets are added to the universe of sets, viz., the pattern of adding a set to the universe, we can gain a sense that it is meaningful to talk about the “universe” of sets as a completed entity, no different from how we talk about the set of natural numbers as a completed entity; in both cases it is meaningful because the infinite collection to which we refer is countable. If we wished to include, along with sets that contain a finite number of elements, sets that contain a countably infinite number of elements, we may include in lieu of the actual completed set, which is an impossibility, a statement of the pattern, or finite algorithm, used to produce the set, or, in other terminology, the “property” that the elements of the infinite set all have in common. If we desire to call such a collection that includes both finite sets and properties a “class,” or just the latter a “class,” or anything else, then so be it – using a different term such as “class” for some aspect of this expanded collection does show a certain recognition of the fundamental distinction between finite sets and countably infinite sets, in that the one is legitimately a completed totality, while the other is not. Then, if we wished to included ungrounded, i.e., non-well-founded, sets, we could do so as well, by replacing each particular infinite regress within a set or within an element of a set, or an element of an element, etc., with the statement of the finite pattern or algorithm used to produce the infinite regress. This is no different from including these finite patterns at the “top” level of the universe of sets to represent countably infinite sets such as the naturals or rationals, since these infinite regresses are, if we wish them to be logically valid, also countable. Beyond this, there is nothing else that could be included. Since the concept of uncountable sets is a logical contradiction, such sets are not sets at all, and so it would not make sense to include them in the universe of sets. We may build this universe in the following way: for the moment, do not consider the specific nature of the finite elements within each set, whereby, e.g., a set of three chickens would be different from a set of three tomatoes; consider for the moment that there is only one set, a set with exactly three individual elements, that represents both of these. Then, taking into account the comments above regarding using statements of pattern to represent countable infinities, what counts as “a set” in the universe of sets is based on the number of elements, the structure of each element – whether it is an individual or a set – and the level of nesting and number and structure of elements within each element. Then, we may add to this by saying that sets with the same number and structure of elements but with different specific elements, such as the sets {1, 2, 3} and {4, 5, 6} or a set of three chickens and a set of three tomatoes, and sets with overlapping elements but that are not identical, such as {1, 2, 3} and {2, 3, 4}, are different sets. Then, we may say that two instances of a set with the same number and structure of elements and the same specific elements, such as two different instances of the set {1, 2, 3}, represent the same set. We may also say that it is possible for an infinite set to exist that “contains” a countable number of physical objects, not as a physically completed set, but, like a countable set of numbers, as a logically valid conception, such as a countably infinite set or collection of tomatoes. Finally, we may say that two sets with different permutations of elements but the same combination of elements would also be considered the same set, though if we really wanted to we could consider each permutation as its own set, and this would still result in only a countable number of sets in the universe of sets.
With regard to early criticisms of Cantor’s theory of the infinite, Potter states, “Some years after Cantor’s work Poincaré … could still assert that ‘there is no actual infinite; the Cantorians forgot this and fell into contradiction.’ On the issue of bare consistency, however, Cantor’s views did eventually prevail: hardly anyone would now try to argue that the existence of infinite collections is inconsistent: the modern finitist is more likely to make the much weaker claim that there is no reason to suppose they exist.”175 The problem here is that when two fundamentally different things, one finite and the other infinite, are so similar and can be so easily conflated, as the finite pattern that produces an infinite sequence can with the infinite sequence so produced, and when this ease of conflating is combined with a powerful emotional drive to finitize the infinite, it is not exactly surprising that on the basis of something so “simple yet powerful” as Cantor’s diagonal argument we are able to gloss over this essential inconsistency in our ideas, so that the vast majority of practitioners either do not think about it at all or see it as at most inconsequential. There is an essential inconsistency here, and it is the same inconsistency that we have discussed throughout this paper, the inconsistency on which the persistent opaqueness and intractability of CH is based. In the realm of countable infinity, which is a logically valid conception of infinity, and thus in the realm of pattern, set theorists have found a way to believe that infinity can be finitized, and their elation at being able to, in this way, “bring infinity into the realm of the circumscribable,” combined with the supposed unassailability of Cantor’s diagonal argument, has made them less careful than they should be in ensuring the logical validity of their underlying assumptions. There have always been those who take the stance that the notion of a completed infinity is a contradiction. But what kept the subject of CH open for so long is that whenever someone doubted, they could always think back to the supposed definitiveness of the diagonal argument, and there stop, because the argument seemed so clear and undeniable. Then, with renewed strength, they could go back to pondering the nature of uncountable infinity, and at the same time go right back to not making any real progress in understanding it. The inconsistency in the conception of a completed infinite collection is not that countable infinity cannot be logically understood. It is that the pattern which we use to create the infinite sequence of elements is itself a finite thing, a fixed algorithm with a particular, fixed number of steps, and because we can comprehend this finite pattern as a completed whole, we draw the erroneous conclusion that we must, therefore, also be able to comprehend the infinite sequence which it produces as a completed whole. But this is to conflate the finite with the infinite, and, therefore, to commit a logical error. Without a clear understanding of this distinction, we cannot see Poincaré’s criticism in its full light. Potter’s comment is more of a historical statement about a trend among practitioners than a statement of his own opinion on the matter. But note that he does not explicitly say that Poincaré was right, or that he was wrong. Potter seems to be caught between a rock and a hard place. Poincaré was one of the most insightful mathematicians in history, so his criticisms and conclusions about Cantor’s theory of the infinite cannot simply be dismissed as ill-thought-out or amateur; further, there seems to be this nagging doubt, often vaguely-felt, that keeps reappearing in various, sometimes unexpected, ways about the coherence of certain important concepts in modern set theory. On the other hand, much of mathematics uses countably infinite sets on a regular basis without logical contradiction, the most broadly accepted version of set theory today assumes that the uncountably infinite exists, and the diagonal argument seems definitive. What, then, is a philosopher to do? Without a clear understanding that the theory of the transfinite and the uncountably infinite rests on a logical error, there is no resolution to this conflict. But once we have this understanding, we can see that Poincaré was right. However, this understanding has to be clear and thorough, rather than partial. In other words, one must not only see the essential truth that there is a logical error at the foundation of the theory of the transfinite and the uncountably infinite, but must also traverse the implications of this essential insight wherever they lead, and be willing, if necessary, to dig up deeply-entrenched, time-honored roots in order to expose a hidden disease that would, if left unchecked, eventually spread and kill the host organism. Philosophy is about uncovering the truth, regardless of how many wish to disbelieve the truths so uncovered. We must be careful not to let idols of our time, or the desire to preserve the imagined nobility and purity of past (or present) golden eras, such as that of “Cantor’s paradise,” prevent us from thinking clearly about our chosen subject matter. In the long run, we gain by making the necessary short-term sacrifices in order to perceive unpleasant aspects of the world correctly, not by striving to find ways to allow ourselves to continue perceiving these aspects in pleasantly distorted grandeur, or to allow these aspects to entirely evaporate before our mind’s eye so we can completely forget that they exist.
Potter states, “Indeed, it is not even clear that we have any direct intuitions that bear directly on the cardinality of the real line beyond the bare fact that it is infinite. Hodges … has remarked (in the course of an interesting discussion of amateur criticisms of the proof) that when we come to Cantor’s result, ‘all intuition fails us. Until Cantor first proved his theorem … nothing like its conclusion was in anybody’s mind’s eye. And even now we accept it because it is proved, not for any other reason.’”176 But in light of what has been shown in the present paper, we can understand why we do not seem to have any “direct intuitions” regarding the cardinality of the real line aside from the fact that it is infinite. We can also understand why Hodges concludes that all intuition fails us when it comes to understanding the reason why Cantor’s diagonal argument is correct. Hodges says that we simply accept the result now not based on an intuitive understanding of why it is correct, but simply because it is correct, and this because it is clearly “proved.” But the reason why there is so much opaqueness with regard to the underlying reason for the correctness of Cantor’s diagonal argument is that it is a flawed argument to begin with. It is literally impossible to understand something that has a logical error contained in it. The difficulty with regard to determining the cardinality of the real line, i.e., the opaqueness in which this question is couched, is the result of the same logical error that prevents us from intuitively understanding why Cantor’s diagonal argument is correct, viz., the flawed assumption (based originally on the diagonal argument itself) that there are different levels of infinity. There will always remain the problem of understanding the “cardinality of the continuum,” and there will always be opaqueness with regard to why Cantor’s diagonal argument is “correct,” so long as we persist in assuming that multiple levels of infinity exist, and that it is legitimate to conflate the finite with the infinite. Progress in foundational matters cannot be made on the basis of logical errors.
In the case of two finite sets, they are equinumerous if they have the same number of elements, and one finite set is more numerous than another if its number of elements is strictly greater than the number of elements of the other set, and, in particular, a finite set which is a proper subset of another finite set has a strictly lower number of elements than the encompassing set, and so the two sets are not equinumerous. Potter make reference to “the fact that … the set of natural numbers properly contains the set of even numbers and yet is equinumerous with it.” He then goes on to say, “The definition of equinumerosity gives rise to a coherent notion of size for infinite sets, therefore, but it is not yet clear that it is a fruitful one. For that to be so, one further thing needs to be true: there have to be sets of different infinite sizes. It is this that is quite unexpected, which is why Cantor’s discovery of the existence of uncountable sets is pivotal.”177 One problem with these conceptions is that the set of natural numbers, or any countably infinite set, does not, and cannot, have a magnitude or particular number of elements in the same way a finite set can. The assumption that this is the case is nothing but wishful thinking. The reason why the even numbers are properly contained in the naturals and yet “equinumerous” with the naturals is not that both have the same number of elements, but that both are infinite sequences, and as such they can both be taken as high as we like, with neither ever ending. The attempt to make these two sequences finished or completed collections of elements having the same total number of elements whose cardinalities can then be compared and found to be equal is based on the desire to finitize the infinite, and is an effort which, if “completed,” produces a logically erroneous result. An infinite sequence is one which grows without bound, and thus is one whose total number of elements is always changing. It is logically contradictory to say that a sequence whose number of elements is always changing could ever have a fixed total number of elements, but it is precisely the latter that is necessary for a set to be able to have a cardinality which can be compared to the cardinality of another set. Potter is correct in saying that if the idea of equinumerosity is to be useful in defining the sizes of infinite sets, there must be infinite sets of different sizes, the way there are finite sets of different sizes; otherwise, the concept of equinumerosity has no value in comparing infinite sets, since such sets would all have the same “size.” But just because the concept of equinumerosity is valuable as a tool to compare finite sets does not mean that it is reasonable or meaningful to extend this concept to infinite sets, sequences, or collections. The desire to do so itself springs from a desire to conquer the infinite, but, again, just because we wish something were possible does not mean it is. If Cantor’s diagonal argument were valid, then this would, as Potter implies, make the concept of equinumerosity valuable in the study of infinite sets. But, as we have seen, Cantor’s diagonal argument is flawed, and, therefore, since there is only one type of infinity, viz., countable infinity, and since it is not meaningful to say that an infinite set has a cardinality, we must conclude that the concept of equinumerosity is not a valuable tool for studying infinite sets.
Potter calls the idea that all infinite sets have the same cardinality “a naive conjecture.” He then goes on to say that the cardinality of the naturals and the cardinality of the reals have already been shown to be unequal, and “so the theory we erect [regarding the use of equinumerosity to study infinite sets] cannot be as straightforward as the naive conjecture suggests.”178 But actually, it can, and it is. The proof to which he refers that these two sets of numbers have different cardinalities makes use of a number of ideas, but its key components are on pp. 117-18 and 121-22 of his book, where he states that (a) there exists a (pure) countable line (Theorem 7.1.1), (b) there is a (pure) countable line of lowest possible birthday that we dub the rational line (a definition), (c) every countable line is isomorphic to (and thus has the same number of elements as) the rational line (Theorem 7.1.2), (d) the rationals are not complete (Proposition 7.3.1), since there are also the irrationals, (e) any complete line is uncountable (Corollary 7.3.2), since the irrationals make a complete line greater in magnitude than the rationals by themselves, which are already countable, and (f) after defining a continuum as a complete line with a countable dense subset, we define the real line as some (pure) continuum of lowest possible birthday.179 The term “pure” here just means that it is assumed that there is no such thing as an “individual” which is a separate type of entity from a “set,” i.e., that even individuals are treated as sets, specifically that each individual is conceived as a set with a single element; the term “birthday” is an artifact of Potter’s particular way of building sets by the use of “levels,” in which a particular set’s birthday is the lowest level in the hierarchy at which the set can appear. This argument has several flaws, and the main one is that it implicitly assumes that countable infinity can be fully counted. Yes, the rationals are countable, but this does not mean that the rationals form a complete set that can be fully counted, and thus whose cardinality can be superseded. In fact, they cannot, because there is an infinite number of them. The fact that we talk of them as a whole, as “the rationals,” makes it easier to erroneously conclude that it is valid to think of them as a totality that can be characterized or measured by means of a fixed cardinality, viz., the “total number” of rationals, when, in fact, this is impossible. In other words, yes, the rationals are countable, but what this means is precisely that their total number cannot be fully counted, because no matter how many of these numbers we add to our growing set of rationals, we can always add more. In other words, again, countable infinity never ends, and so there can never be anything beyond it. As we have discussed in earlier sections, the reals themselves are countable, because each real, whether rational or irrational, is a fixed magnitude in the total sequence of real numbers, and, as such, each real can be indexed by a single natural number, i.e., the reals can be mapped one-to-one with the natural numbers. The idea that there is somehow a “totality” of natural numbers, and thus of any set that is “isomorphic” to them, such as the rationals, that can be “gone beyond” to reach even higher quantities or numerical values is nothing but the logical error of conflating the finite with the infinite, and such an argument gains unjustified credibility on the back of the supposed validity of the diagonal argument. In fact, the reals themselves are isomorphic to the naturals. This only seems counterintuitive because we are so accustomed to thinking that this is not the case. But it is no different from the difficulty we experience when we first try to grasp the fact that the even numbers can be mapped one-to-one with the naturals. We think, the evens are a proper subset of the naturals, so how could it possibly be the case that there are exactly as many evens as there are naturals? Or for that matter, the same number of units of 1,000,000 as there are naturals, where each million natural numbers is mapped one-to-one with a single natural number? But the question is based on a flawed assumption, viz., that it is logically meaningful to say that the naturals, or the evens, have a particular “number” of elements, even though, of course, we cannot specify what that number of elements actually is. The counterintuitive quality of the idea of equating the number of elements of the evens with the number of elements of the naturals springs from the logical error of assuming that either of these sets has a total number of elements whose fixed value can be compared to the fixed value of the number of elements of another set. This is simply not the case. One gets the impression that, in so cavalierly dismissing the “naive conjecture” that all infinite sets are equinumerous, Potter wishes to not think too seriously or too clearly about this possibility, because if, somehow, it can be shown to be valid, the bulk of modern set theory will thereby have been shown to be logically flawed.
We have said that it does not make logical sense to try to add or multiply infinite quantities, because the operations of addition and multiplications (and other arithmetic operations) only make sense when performed on finite, unchanging quantities. In set theory, it is standard to perform arithmetic operations on infinite cardinals and ordinals. How do such operations have meaning in set theory? They take on meaning by the treating of each number, finite or infinite, as if it were a set. A finite cardinal or ordinal is treated as a set with the same number of elements as the number it represents; a countable infinite cardinal or ordinal is treated as a countable set of elements, i.e., an infinite set of element that can be mapped one-to-one with the natural numbers. Therefore, the addition of two countable cardinals or ordinals can be treated as the addition of two countable infinite sets, which, like the two countable sets of the even numbers and the odd numbers, can easily be seen to “add up” to a countable set by simply taking the numbers in each set alternatingly and putting them into a third set, the “sum” set. We can represent the first set by the infinite number λ, the second set by the infinite number η, and their sum λ + η by the infinite number φ, i.e., λ + η = φ. But what, exactly, have we learned from this? A number is defined solely by its fixed, unchanging magnitude, its value. But since the numbers in question in this addition problem are infinite, they can never have fixed, unchanging values, i.e., they can never be numbers. The only reason that such an “addition” operation seems to make sense is that the infinity represented by the addends is an accurate representation of infinity, i.e., countable infinity, and so we can logically grasp each of the infinite sets as a countable collection of elements. And because each set is countable, we can clearly see that it is possible to create one set to which we may continue adding the elements from both original sets for as long as we like, i.e., it is a logically valid operation to take elements from both sets one (or more) at a time and put them in a new set, i.e., to union the two sets. Such a union operation is similar, or analogous, in certain ways to the process of addition of finite numbers, and so, out of a desire to finitize infinity, we define addition of countably infinite “numbers” by their countable unions. Once we have made this leap, then various other properties, such as associativity, commutativity, identity, distributivity, exponentiation, etc., may be defined on these countably infinite sets and their combinations by the same analogy, which, notably, treats each element of the sets being combined in various ways individually, in order that these definitions of “transfinite arithmetic operations” make at least a certain level of sense – this is something that must be done, because since addition operations and properties only make sense on fixed magnitudes, and since the sets themselves are countable and thus never fixed, in order to define addition operations and properties on these sets we must define them in such a way that the actual concrete tasks of the addition operations only ever happen on one element at a time, i.e., only ever happen on fixed magnitudes. It also helps that, e.g., in the case of two different infinite sets being added, the two sets may have different elements, such as one set being the odds and the other the evens, because this makes it seem more feasible to say that they might represent two “different” infinite numbers; this, in turn, makes it seem less unreasonable to identify different infinite “numbers” in our equations by different symbols, e.g, λ + η = φ, and in the basic properties of ordinal and cardinal addition which we define, and the elementary consequences of these properties, e.g., λ + η = η + λ, or β(λ + η) = βλ + βη in the case of cardinals, or β(λ + 1) = βλ + β or 2ω = ω < ω + ω = ω2 in the case of ordinals (these are random example selected from the list of addition properties of cardinals and ordinals and their elementary consequences; we should note here that we are aware that the addition properties in standard set theory differ in various ways between transfinite cardinals and transfinite ordinals, and so we are not attempting to say here that in standard set theory they are all the same). In this way, we gradually convince ourselves that it is possible to meaningfully extend the concept of arithmetic on finite numbers to the realm of the so-called transfinite.
But this is a logically flawed extension. The only way in which the operations and properties of addition can be meaningful is if they are performed or defined on finite, fixed quantities. Only if the numbers in question are finite is it meaningful to say that there can be two different numbers, because the only property by which numbers are defined, and thus by which they can differ, is the property of magnitude, or, in the language of set theory, cardinality. But if two “numbers” are both countable, then it makes no sense to identify them as two different numbers, by, e.g., using a different letter to represent each, since they are both of the same “magnitude.” At best, we may say that identifying the same number by two different letters represents our lack of knowledge that two unknowns have the same cardinality, and thus are equal; but this is to stretch the limits of credulity regarding what the different letters in these operations in set theory are meant to represent. The implication in these addition problems on countable transfinite numbers is that the different letters do, or at least can, represent different transfinite numbers. But this does not make logical sense, because the different letters all represent countable sets, and thus all have the same “magnitude.” In fact, in defining transfinite addition by means of various combinations and arrangements of the elements of the sets that the transfinite numbers are supposed to be, we are admitting that we are unjustified in treating the transfinite numbers as numbers – if transfinite numbers were numbers, then we would not feel the need to use set representations of them in order to obtain the concreteness of magnitude necessary to perform meaningful arithmetic operations on them; we would simply perform the operations on the transfinite numbers directly, no different from the way we do with finite numbers. This is one of those situations in which an idea, in this case that of arithmetic operations on numbers, starts to breach the bounds of its applicability, but is not yet so far beyond these bounds that we can clearly recognize it as non-applicable. If on top of this we are incentivized by other reasons, such as the powerful emotional drive to conquer infinity combined with the supposed unassailability of the simple yet powerful diagonal argument, to not see that we are breaching the bounds of applicability of the idea, then there is a higher chance that we will not see that we are breaching these bounds and will instead continue to believe that we are making logical sense in our arguments and conclusions.
As stated, the addition operation itself does not make sense on transfinite numbers because addition is only meaningful on finite quantities. To say that it is meaningful on infinite quantities by defining the sum of two countably infinite sets to be their union is to strip the entire meaning of the concept of “addition of two numbers” from the addition operation, so that the sequence of symbols of a cardinal or ordinal addition operation is in reality nothing but a parody or mimicry of addition, not a legitimate representation of it – an emperor with no clothes. The ideas and procedures of cardinal and ordinal arithmetic are nothing but another attempt to finitize the infinite, no different from treating an infinite decimal sequence as if it is equal to its limit point. The effort to try to create an equivalent of finite-number addition in the realm of the infinite is an effort to achieve the impossible, and so is doomed to failure. The analogous form of the basic arithmetic operations in the transfinite numbers may be meaningful in certain ways if each such “number” is treated as a countably infinite set, but it is disingenuous at best to call such operations addition or multiplication or exponentiation, etc., because this implies an equivalence with these operations on finite numbers when there is, in fact, no equivalence, only superficial similarity. Also, the “success” of translating addition operations to the countably infinite bolsters the idea that it is possible to translate such operations into the uncountably infinite as well. But this, also, would be a logical mistake, not only because the “success” in translating the operations into the countably infinite was not, in fact, an actual success, but because, as we have discussed, the concept of the uncountably infinite is itself logically flawed.
It is interesting to note that in comparing ordinal and cardinal exponentiation Potter states that if we could “define ordinal exponentiation in a way that matched it up with cardinal exponentiation,” then “we would in particular … have defined a well-ordering on [the power set of ω]. But this is known to be impossible to do in our theory, even if we include the axiom of choice… .”180 So, in our definitions of ordinal and cardinal exponentiation, we explicitly rule out the equating of the two on the basis of the fact that if we did equate them the reals would be well-orderable, i.e., they would “behave very much like natural numbers [in that] they [would be] linearly ordered by [inclusion], and every nonempty subset [would have] a least element. We call linear orderings with this property well-orderings … .”181 (First italics mine.) In other words, such “matching up” would lead to the conclusion that the reals are countable, which in modern set theory is an unacceptable result; we have already “shown” that the power set of ω has cardinality equal to that of the continuum and that this cardinality is uncountable, and thus the equating of the operations of cardinal and ordinal exponentiation would appear to result in a contradiction. But, if there is no such thing as uncountable infinity, then this roadblock in the way of equating the operations of ordinal and cardinal exponentiation is removed. However, this is not all: if there is no such thing as uncountable infinity, then there is no such thing as an end to countable infinity, and thus the operations of ordinal and cardinal exponentiation both reduce to the logically valid expression of exponentiation, viz., that on finite numbers, and, as such, the operations of ordinal and cardinal exponentiation become equivalent. In other words, the idea that ordinal and cardinal exponentiation are different is an outgrowth of the logically flawed idea that it is valid to conflate the finite and the infinite, as well as of the different idiosyncratic ways in which ordinal and cardinal exponentiation are defined on the basis of various results that follow from this conflation. Remove the logical flaw, and we can see that exponentiation is a singular process, not one that can bifurcate to mean different but related things for different “types” of infinite number.
Potter states, “We have proved that 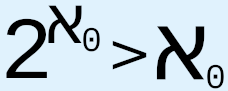 . But is this true in the same sense that 4 > 2? From a narrowly formal perspective, of course, we can give a positive answer to this question, since both are instances of Cantor’s theorem. But that only answers the question to the extent that the formalism in which the common proof of the two inequalities is formulated has a sense. What we really wanted was to be taught how to think about infinite sets, and the answer which the theory urges upon us is that we should think of them, as far as possible, as being just like finite sets. But how far is that? Analogy is one of the most important tools in mathematical thought, but the analogy we are dealing with here is one that we can be sure will at some point fail us.”182 Exactly. Here Potter shows his philosophical side, which steps outside set theory proper and tries to understand its meaning and significance. Potter expresses his sneaking suspicion that the extension of the processes and ideas that were formed in the realm of the finite into the transfinite might not be all it is cracked up to be. We may first recall that the expression
. But is this true in the same sense that 4 > 2? From a narrowly formal perspective, of course, we can give a positive answer to this question, since both are instances of Cantor’s theorem. But that only answers the question to the extent that the formalism in which the common proof of the two inequalities is formulated has a sense. What we really wanted was to be taught how to think about infinite sets, and the answer which the theory urges upon us is that we should think of them, as far as possible, as being just like finite sets. But how far is that? Analogy is one of the most important tools in mathematical thought, but the analogy we are dealing with here is one that we can be sure will at some point fail us.”182 Exactly. Here Potter shows his philosophical side, which steps outside set theory proper and tries to understand its meaning and significance. Potter expresses his sneaking suspicion that the extension of the processes and ideas that were formed in the realm of the finite into the transfinite might not be all it is cracked up to be. We may first recall that the expression 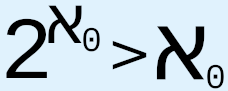 is not a logically valid expression; it is for this reason that this inequality does not express the same thing as the inequality 4 > 2. We have discussed at length the fact that
is not a logically valid expression; it is for this reason that this inequality does not express the same thing as the inequality 4 > 2. We have discussed at length the fact that 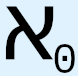 is not a number, because a number’s sole defining characteristic is that it is a fixed, finite value, and
is not a number, because a number’s sole defining characteristic is that it is a fixed, finite value, and 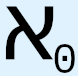 by definition represents an infinity, that is, something that is ever-changing. Cantor’s theorem that the power set of a finite set of elements is greater in magnitude than the original set is a logically valid conclusion, and it can be proved rigorously by using standard mathematical induction. But this logically valid conclusion cannot be extended to say that the magnitude of the power set of an infinite set is greater than the magnitude of the original infinite set, because it does not make logical sense to assign to an infinite, that is, an ever-growing, ever-changing, set, a fixed magnitude; and it also does not make logical sense to raise a finite number, such as 2, to the power of the magnitude of an infinite set, since the process of exponentiation is only meaningful when both the base and the exponent are finite, i.e., fixed, magnitudes. In other words, to answer Potter’s first question, the former inequality is not true in the same sense as the latter inequality not because the former inequality is true in a different way than 4 > 2, but because the former inequality is logically meaningless, and thus cannot be assigned a truth value at all. This is the reason for the confusion and vagueness in trying to understand the way in which the former inequality is true. In other words, even at this early stage we are already at a point where the analogy between finite and infinite sets fails us. The two inequalities can both be “proven” to be true in the same set theoretic formalism only because this formalism itself is already partly based on the logically invalid assumption that it is possible to finitize the infinite, and thus that we may treat infinities as finite things, that is, think about them and manipulate them in our formulas and proofs as if they were finite. Once we correct this logical error at the foundation of set theory, we can see that only the latter inequality can be validly proved, and thus assigned a truth value, and that the former cannot because it references ideas and entities which are logically flawed. The analogy between the finite and the infinite in set theory fails us precisely at the point where we start treating the finite as if it could be equal to the infinite, in any way. To be logically valid, set theory can only contain (a) finite sets, and (b) countably infinite sequences of elements produced by finite patterns which, for convenience, we may call “infinite sets.” In this, we must always keep in mind that these countably infinite sequences can never be completed wholes, because this would contradict the meaning of the word “infinite.” Further, anything at all beyond this would introduce logical errors, and thus cannot be brought into the picture if we wish to remain logically consistent in our theory. Potter seems to have an intimation of an inkling that all this might, in fact, be the case. But he does not bring such considerations out into the open so that they may be analyzed in detail. He does not, in other words, take this intimation and follow it conceptually to its logical conclusion.
by definition represents an infinity, that is, something that is ever-changing. Cantor’s theorem that the power set of a finite set of elements is greater in magnitude than the original set is a logically valid conclusion, and it can be proved rigorously by using standard mathematical induction. But this logically valid conclusion cannot be extended to say that the magnitude of the power set of an infinite set is greater than the magnitude of the original infinite set, because it does not make logical sense to assign to an infinite, that is, an ever-growing, ever-changing, set, a fixed magnitude; and it also does not make logical sense to raise a finite number, such as 2, to the power of the magnitude of an infinite set, since the process of exponentiation is only meaningful when both the base and the exponent are finite, i.e., fixed, magnitudes. In other words, to answer Potter’s first question, the former inequality is not true in the same sense as the latter inequality not because the former inequality is true in a different way than 4 > 2, but because the former inequality is logically meaningless, and thus cannot be assigned a truth value at all. This is the reason for the confusion and vagueness in trying to understand the way in which the former inequality is true. In other words, even at this early stage we are already at a point where the analogy between finite and infinite sets fails us. The two inequalities can both be “proven” to be true in the same set theoretic formalism only because this formalism itself is already partly based on the logically invalid assumption that it is possible to finitize the infinite, and thus that we may treat infinities as finite things, that is, think about them and manipulate them in our formulas and proofs as if they were finite. Once we correct this logical error at the foundation of set theory, we can see that only the latter inequality can be validly proved, and thus assigned a truth value, and that the former cannot because it references ideas and entities which are logically flawed. The analogy between the finite and the infinite in set theory fails us precisely at the point where we start treating the finite as if it could be equal to the infinite, in any way. To be logically valid, set theory can only contain (a) finite sets, and (b) countably infinite sequences of elements produced by finite patterns which, for convenience, we may call “infinite sets.” In this, we must always keep in mind that these countably infinite sequences can never be completed wholes, because this would contradict the meaning of the word “infinite.” Further, anything at all beyond this would introduce logical errors, and thus cannot be brought into the picture if we wish to remain logically consistent in our theory. Potter seems to have an intimation of an inkling that all this might, in fact, be the case. But he does not bring such considerations out into the open so that they may be analyzed in detail. He does not, in other words, take this intimation and follow it conceptually to its logical conclusion.
Potter states that CH is decided in second-order set theory, i.e., in second-order predicate logic. But, as we have discussed, second-order logic brings the concept of uncountable infinity into the picture, and as such cannot be trusted to give valid answers when such a concept is used in its statements and proofs. In particular, since CH itself is a question about uncountable infinity, we may expect that (a) second-order logic would have something to say about CH, given that second-order logic assumes uncountable infinity exists, and (b) whatever is said by second-order logic about CH will be meaningless, because such conclusions would be based on logically flawed assumptions. Indeed, Potter himself, though he does not say it quite this way, does say, “The difficulty [with what second-order logic could say about CH] is evidently that in contrast to the case of the axiom of choice we do not seem to have any intuitions about whether these second-order principles that could settle the continuum hypothesis are themselves true or false. So this observation does not seem especially likely to be a route to an argument that will actually settle the continuum hypothesis one way or the other.”183 What could be the reason for this lack of intuition regarding the truth status of the second-order principles? But we have already given the answer: logically flawed ideas are intrinsic in the formulation of second-order logic, and such ideas are inherently non-understandable.
Potter then discusses Kreisel’s 1971 assertion that the place of CH in set theory is not like the place of the parallel postulate in geometry, but more like “the proven insolubility in elementary geometry of the classical problems of squaring the circle and trisecting the angle: what is shown is not that an angle cannot be trisected but only that it cannot be done with a straightedge and compasses. But even if this analogy is apposite, it is not clear that it helps us to solve the continuum problem, since it does not give us much of a clue where to look for the new methods that we need.”184 But this analogy is not apposite. Kreisel’s assumption is that CH can be solved, the way it is possible, and logically meaningful, to square a circle or trisect an angle, and it is simply that new or different methods or ideas of which we are currently unaware are needed. But as we have seen, CH is based on logically flawed concepts, and thus it is impossible to solve it, i.e., to assign to it a truth value.
Potter then briefly discusses the projects in set theory to find a way to prove or disprove CH by the addition to set theory of ever larger cardinals via ever stronger axioms of infinity. However, after numerous failures over the years this method is now considered to be “very unlikely” to be successful at determining a truth value for CH: “Broadly stated, every large cardinal axiom so far proposed is known not to settle the continuum hypothesis.”185 Is it possible that some cardinal that is even larger than all that are currently known will be able to solve CH? But the answer must be no, because these cardinals represent uncountable infinity, which is a logically flawed concept, and because, again, CH itself makes direct reference to uncountable infinity, and also assumes it is meaningful to attempt to equate the magnitudes of infinite, ever-changing values, and so itself is logically flawed. It is impossible to use logically flawed concepts to prove anything, whether what one is trying to prove is itself logically valid or not.
Potter then briefly discusses Gödel’s conclusion that “no formal characterization is possible of what should count as an axiom of infinity.”186 Potter mentions Gödel’s basic high-level comment regarding the nature of such a characterization, and then says that neither Gödel nor anyone else has actually published a candidate for this formal structure. But this all might be expected, since axioms of infinity beyond the basic one in ZFC all reference the concept of uncountable infinity, and so a logically valid general description of such axioms, i.e., a logically valid “formal characterization” of them, is impossible. By viewing these comments and (the lack of) results in light of the ideas we have been discussing in this paper, we can readily explain why things have turned out the way they have.
Potter discusses Gödel’s brief speculation “that there might be no strongly undecidable propositions in set theory,”187 i.e., no propositions that cannot be proven true or false in the context of a suitably strong axiom of infinity combined with a certain hitherto unknown axiom regarding the completeness or largeness of the universe of sets. Without additional research, it is hard to know the full conceptual context in which Gödel made this speculation. But in a way this may be interpreted as Gödel briefly seeing the truth about infinity, if only in a roundabout way. There are, in fact, no strongly undecidable statements in set theory when set theory is restricted to that part of its current form which is logically valid, and this is because there are no logically valid numbers above the finite numbers, and so there are simply no valid axioms of infinity beyond the (correctly understood) base axiom of infinity regarding countable infinity in ZFC and which could thus be added to ZFC without at the same time adding a logical contradiction. In other words, there is no such thing as a logically valid proposition that is so “strong” that no level of infinity, no matter how high, could be added to ZFC that would prove or disprove it.
In a comment on Cohen’s comment that the cardinality of the continuum must be greater than any uncountable cardinal we could construct, or possibly even conceive, Potter quotes Scott as saying, “‘we would be pushed in the end to say that all sets are countable (and that the continuum is not even a set!) when at last all cardinals are absolutely destroyed.’”188 The point to be made here is that the idea that all sets could be countable seems to be almost a sacrilege to Scott, a very extreme position that one can do nothing but marvel at. And so, presumably, would the majority of set theorists conclude today. We may say that a large part of this incredulity is due to the emotional and psychological implications of the idea that all logically valid sets are at most countable, specifically that if this is true then all our effort to mathematically capture the infinite will have been for naught, i.e., we will end up realizing that we have come no closer to capturing infinity than when Cantor began this effort 150 years ago. These are serious emotional and psychological implications, and so we are highly incentivized to find ways to believe that the idea of uncountable infinity is acceptable, normal, desired, interesting, logically valid, etc., and that the idea that there is nothing beyond countable infinity is abnormal, absurd, non-intuitive, amateurish, logically unsatisfactory, beyond the pale, etc. Emotional need drives what we consider or believe to be possible or impossible to a much greater degree than we often realize. It is the purpose of rational analysis to bring to light and to criticize false conclusions which we draw that we believe to be true, and this is the case for false conclusions drawn on the basis of emotional need just as much as on the basis of simple mistakes in the logic of an argument.
Potter states that “one reason for the tendency of mathematicians to regard the continuum hypothesis as absolutely undecidable may well be that it receives so little regressive support from its consequences.”189 This reasoning is on the right path. The reason CH has so little regressive support is that it is a logically flawed statement based on logically flawed conceptions, and such statements and conceptions will not find a home in logically valid mathematical systems and results.
In discussing Feferman’s view of the “inherently vague” nature of CH, Potter says that “if we admit the continuum hypothesis as vague, we shall be hard pressed to resist the conclusion that all other sentences involving quantification at the third infinite level of the hierarchy are more or less vague as well.”190 Exactly. If a system of logic is based on the logical flaw of conflating the finite with the infinite and the nonsensical concept of uncountability, then any statement or conclusion in this system of logic that makes use of these invalid ideas will also be logically flawed, thus not representative of reality, and thus not intuitively understandable, i.e., it will be vague. Potter then quotes Steel: “ ‘There may be something in the idea that the language of third order arithmetic is vague, but the suggestion that it is inherently so is a gratuitous counsel of despair. If the language of third order arithmetic permits vague or ambiguous sentences, then it is important to trim or sharpen it so as to eliminate these.’ ”191 Exactly, at least with regard to the last sentence. However, it would probably not be unreasonable to say that Scott does not consider uncountable infinity to be a logically flawed concept, so in his acknowledgment that there may be certain ways to trim or sharpen third order arithmetical logic to make it a little clearer, he presumably is not considering the more radical possibility of eliminating the notion of uncountability altogether. But it is this, in fact, that needs to be done if we are to remove the “vague,” or logically flawed, ideas and conclusions from second- and higher-order logic. Whether there will be anything left of these higher levels of logic after such removal, or whether, with perhaps certain minor modifications of first-order logic, they will be more or less reduced to first-order logic themselves, we may with interest speculate. But in criticizing Feferman, Steel himself does not show, at least in this small passage, that he has any more insight into CH or other such conundrums than Feferman does. In particular, Scott criticizes Feferman’s likening of an arbitrary set of reals to “ ‘the ‘concept’ of a feasible number,’ ” after which he goes on to say, “ ‘This analogy is far-fetched at best. The concept of an arbitrary set of reals is the foundation for a great deal of mathematics, and has never led into contradiction. The first two things of a general nature one is inclined to say about feasible numbers will contradict each other.’ ”192 Of course, when the reals are treated as, and thought about as, fixed magnitudes, and thus as completed, finite entities, then the concept of an arbitrary set of reals does not cause problems in broader mathematics, because this is a logically valid way to think about a set of real numbers; and, in particular, this way of thinking about real numbers entails, as we have discussed, that the reals are countable. But this completely sidesteps the key point of Feferman’s comments about the vagueness of the concept of an arbitrary set of reals. The vagueness arises because we have it in our heads that the reals are greater in number than the naturals, i.e., that the naturals are countable but that the reals are somehow greater than this in totality, and also that it is possible for there to be a “totality” of naturals and a “totality” of reals as finished or completed sets. When we overlay these logically flawed concepts onto the logically valid concept of the real numbers as finite, fixed magnitudes, things become confused where once they were clear, because logically flawed concepts are inherently non-understandable. In saying that arbitrary sets of reals have been much used in broader mathematics without contradiction, Scott implicitly restricts his criticism to the logically valid conception of the reals, thereby completely ignoring the key point of Feferman’s argument. In doing this, Scott renders his criticism irrelevant. Further, Scott does not see that this is the case because he is still in the grip of the flawed belief that there is no logical error in the ideas of finitized infinity and uncountability, and so he implicitly believes that any comment he makes about the logically valid conception of the real numbers must also apply to the logically flawed conceptions of them, i.e., he implicitly treats the logically valid and logically flawed conceptions as equal to each other, and as both logically valid. Note also that this is the case regardless of whether Feferman’s analogy to ‘feasible numbers’ is a valid analogy.
Potter quotes Fraenkel and his co-authors in a 1958 work saying that “when we try to reconcile the image of the ever-growing universe with our desire to talk about the truth or falsity of statements that refer to all sets, we are led to assume that some temporary universes are as close an ‘approximation’ to the ultimate unreached universe as we wish. In other words, there is no property expressible in the language of set theory which distinguishes the universe from some ‘temporary universes.’ ”193 But set theory already contains examples of the essential component necessary to include all logically valid sets within it, and this component is expressed, albeit in somewhat disguised form, in the symbols that represent the standard infinite sets – ℕ, ℚ, $#x211d;, etc. In set theory, each of these symbols is used to represent both a finite pattern that produces an infinite sequence, and the infinite sequence so produced. We only need a clarified understanding of infinity and then we can properly tease apart the pattern from the sequence and see that the pattern itself, which is a logically valid finite representation of an infinite sequence, is a finite expression of the totality of an infinite set of numbers; and we can realize that all our attempts to understand the uncountably infinite are attempts to understand a mirage, which mirage makes us erroneously think that there must be levels of logical truth, or in any case levels of “higher” truth, that we, as humans with “finite” minds, have no capacity to grasp. For a person of the religious persuasion, such an “ungraspable” truth may be equated with God, or with whatever the “ultimate” is conceived to be in their particular religious tradition. But the reality is that there is nothing higher than “mere” or “simple” countable infinity, however much we may wish this were not so. The reason why there seems to be an ungraspable aspect to uncountable infinity, and why no matter how high a level we go to or how accurate our approximation is to the full universe of sets, we can always go higher, or add more, or progress beyond the given level, and thus can never fully “complete” the universe of sets, is precisely because this quality of being “never complete” is the essential nature of countable infinity; and countable infinity has been, through various rounds of individual and collective mental gymnastics, superimposed onto the conception of uncountable infinity and sequences of countable and uncountable ordinals and cardinals, so that we now treat these sequences as if they behaved more or less no differently from countable sequences of finite numbers. Mathematics attempts to make the patterns of the world understandable, but it is inevitable that when we see a pattern we understand that it eventually ends and thus can be repeated, which is part of the nature of a pattern. So when we see a pattern with regard to numbers in mathematics, we can see that this pattern, too, can be repeated, and thus can be repeated as often as we like. But this leads directly to the idea of countable infinity. And since mathematics is supposed to bring the world into the realm of the understandable, i.e., to finitize, in a certain important intellectual sense, the world, we are at once faced with a paradox – how do we finitize something which is clearly infinite? The real answer is that, of course, it is impossible to finitize the infinite. But our desire for certainty at a deeply powerful emotional level drives us to try to finitize the infinite anyway, and to try to find ways to ignore or downplay or trivialize the logical errors that stand in the way of this effort. We equate infinite sequences of numbers with the finite patterns that produce them, and use this to feel as if we have at least partly conquered the infinite. But as soon as we create a clear enough finitization of an infinite thing, which means that we now treat the infinite thing in a nontrivial way as if it were finite, we immediately see that we may go beyond this finitized infinite thing, precisely because the essence of infinity has been stripped from it, and so, in the relevant ways with respect to our overall effort to finitize the infinite, the infinity has become finite in our thoughts and treatments. When something becomes finite, of course we may see a way to go beyond it, because it is now finite, and the definition of “finite” is the quality of being fixed, which by its nature is something we may go beyond. Therefore, in finitizing the infinite we have not solved our problem, to any degree; all we have done is create something that is finite itself, which is equivalent to completely negating the entirety of our effort, i.e., losing every bit of ground that we thought this whole time we had been gaining. This is exactly what has happened and continues to happen in the theory of transfinite numbers and uncountable infinity. The set of reals, for example, is conceived to be uncountably infinite, and thus, in some nebulous way, we are “even more” unable to complete or finitize this infinity than we are countable infinity. And yet, the reals are treated as a completed collection, and as having their own cardinality, i.e., their own fixed magnitude or total number of elements. But as soon as we start thinking about the reals in this way, it becomes more feasible that there could be levels of infinity beyond that of the reals, because, after all, the reals do have a “total” number, even though we may not clearly understand what that number is or how to find it. This is the case with the sequences of ordinals and cardinals in general, both countable and uncountable. As soon as we start treating these infinities as finite things, it is inevitable that we will be able to go beyond them, ad infinitum. This, then, is a conundrum. If this always happens, how, then, will it ever be possible to finitize the infinite in a way that ends up being satisfactory? But the answer is that it is literally impossible to do this, because, by definition, infinity is something that cannot be finitized. We expend so much effort trying to finitize infinity not because it is possible to do so, but because we have a desperate desire to do so, and this desire ultimately springs from our fear of death, as built powerfully into the human psyche by the evolutionary process. If we can grasp infinity, hold eternity in our hands, truly finitize it, then we may be able thereby to become infinite ourselves, i.e., to become immortal, i.e., to conquer death. This is the source of the perpetually renewed effort over the past 150 years to find a way to complete the work that Cantor started. It is a mathematically acceptable way to search for the existence of God, no different from the efforts of the individuals who go into philosophy or science or theology for the purpose of finding a rational proof of God’s existence, out of a recognition that nothing can be logically valid unless it has a rational argument in its favor. This is not to say that all set theorists purposely went into set theory to find proof of God’s existence, or that there are no atheistic or agnostic set theorists. The point is that the search for a way to overcome death, to overcome mortality, expresses itself in many and diverse ways, and in set theory it has found an expression that is particularly mathematical in nature.
In the case of Fraenkel’s comment regarding the impossibility of finding a way in the language of set theory to express the totality of infinity or the totality of sets, we can resolve this by a simple shift in how we think about sets and about infinity. As mentioned, set theory already has an indirect method of encompassing the totality of sets of a particular kind. If we recognize that uncountable infinity is impossible, and that our conundrums regarding the unendingness of uncountable infinity are only a disguised version of the fact that countable infinity is unending, then we may entirely encompass the universe of sets in the language of set theory by (a) having symbolic expressions for finite sets, which set theory already has, and (b) creating symbols that represent the essential nature of pattern (it matters little precisely how this is done), so that whenever we need to talk about a countably infinite sequence as a whole, we can invoke the symbols for pattern in our arguments and proofs. This would also allow for non-well-founded sets to be a part of set theory just as easily as well-founded sets. In doing this, we would have encompassed all logically possible sets in the particular, finite language of this modestly-extended version of set theory. This does not mean we will have finitized infinity – infinity will still be infinite, as always, and thus will remain un-encompassable. But by modifying set theory in this way, we will have come to grips with the actual nature of infinity, and thereby solved the otherwise unsolvable problems which plague us as a result of a flawed, but in certain important ways emotionally comforting, understanding of infinity. Fraenkel and his co-authors were correct in that it is impossible to fully finitize infinity. But they were incorrect in saying (or implying) that the more we capture levels of infinity into ordinals and cardinals, the closer we get to the “true” or “full” nature of infinity. Capturing more and more of something can only get us closer to the true nature of that something if that something is ultimately finite. If something is infinite, then no matter how much of it we capture, there will always be an infinity remaining to be captured, and so no matter how much we capture, we will not have made any progress toward completing the process of capturing, i.e., circumscribing or finitizing. Here, too, we can see an example of the equating of the finite with the infinite. The “set of all sets” and the “universe of sets” are themselves phrases that imply a completion, or finitizing, of something that is infinite, and even just due to the way these phrases are worded we begin to think of a fixed collection of sets as the “universe” of sets that includes all sets. But since the number of sets that can be produced or conceived is infinite, because the elements that are the members of sets, and the sets themselves, are defined in such a way that they can be produced by patterns, which can be iterated as many times as we like, then it is literally impossible to complete the collection of sets, just like it is literally impossible to complete the set of natural numbers. We may think of the totality of sets being completed as a convenience when discussing all sets, but, as with the natural numbers, there is a difference between the pattern that produces additional sets in the collection of sets, viz., the pattern add one more set to the existing finite collection of sets, on the one hand, and the ever-growing collection of sets itself, on the other. If we equate the two, then we start to run afoul of logical errors, such as thinking that by capturing ever-higher levels of infinity in finite symbols we more and more closely approximate the true nature of infinity – running down blind alleys that end in a giant looping circle which leads back to an earlier point in the alley path, but we never realize that the path loops and instead continue to think we are moving straight and making genuine progress toward some ultimate goal where the path will actually end. If we conflate the finite with the infinite, or assume as valid any logical error whatsoever, we will inevitably find ourselves unable to progress beyond a certain point in our investigations, due to the unscalable mountainous peaks that we ourselves have raised up in front of us.
Hrbacek provide a proof that 2ℕ is equal to the cardinality of ℝ.194 They start by defining the “characteristic function,” which maps any subset S of ℕ to an infinite sequence of 0s and 1s such that for each natural number n, if n is in S then its corresponding position in the output of the characteristic function is 0, and if n is not in S then its corresponding position in the output of the characteristic function is 1. For example, for the set S = {2, 5, 6, 9} the characteristic function would output {1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, …}, where the ellipsis represents an infinite sequence of 1s. Since S may be any ordered collection of natural numbers, since each such ordered collection maps to a unique infinite string of 0s and 1s, and since each infinite string of 0s and 1s maps to a unique ordered collection of natural numbers, then there is a one-to-one mapping of the subsets of ℕ onto the set of infinite sequences of 0s and 1s, i.e., the mapping is bijective. The collection of all infinite sequences of 0s and 1s can, for convenience, be written as {0, 1}ℕ, which is analogous to the well-defined operation of exponentiation of a set as it is defined on finite sets with finite exponents; for example,
{0, 1}3 =
{0, 1}⨉{0, 1}⨉{0, 1} =
{{0, 0, 0},{0, 0, 1},{0, 1, 0},{0, 1, 1},{1, 0, 0},{1, 0, 1},{1, 1, 0},{1, 1, 1}}
is the collection, or set, of all possible sequences of 0s and 1s of length 3, and the cardinality of this set is 23 = 8. This procedure is a way to produce a set that always has the same cardinality as the power set of a set of elements whose cardinality equals the value of the exponent, in this case 3, and since there are 2 elements in the set {0, 1}, and the cardinality of the result of the operation {0, 1}3 is the same as 23, when speaking of cardinalities it can be convenient to think of these two expressions as equivalent. By analogy, then, it can also be convenient to say that the total number of different infinite sequences of 0s and 1s, which are the exact sequences produced by the characteristic function, could be expressed by replacing the 3 with ℕ, since, instead of cardinality 3, the sequences produced by the characteristic function for the subsets S are all countably infinite. We could, in other words, say that the total number of sets produced by the characteristic function is 2ℕ, and that, therefore, the total number of such sets is equal to the cardinality of P(ℕ).
The rest of the proof consists of showing that the cardinality of ℝ is less than or equal to the cardinality of P(ℕ) and also greater than or equal to the cardinality of 2ℕ, so that by the squeezing property all three cardinalities must be equal. First, they use the Dedekind cut definition of the reals to say that each real is mapped to uniquely by at least one infinite sequence of rationals. However, since the collection of all infinite sequences of rationals is a proper subset of the power set of the rationals, or since more than one infinite sequence of rationals can map to a given real – either is appropriate – we may say that the cardinality of the reals is less than or equal to the cardinality of the power set of the rationals. But since the rationals are countable and thus their cardinality is equal to that of the naturals, the cardinality of the reals can be said to be less than or equal to the cardinality of the power set of the naturals. Then, to complete the proof, they use, just as the diagonal argument does, the infinite decimal sequence representation of real numbers. First, we are to think of each unique infinite sequence of 0s and 1s as a unique decimal number in the interval (0, 1). But then the entire collection of these infinite sequences of 0s and 1s maps into the reals, but not onto them. Therefore, since the set of all infinite sequences of 0s and 1s has cardinality 2ℕ, the magnitude 2ℕ is less than or equal to the cardinality of the real numbers. Finally, by applying the squeezing property within ℝ in the middle, the cardinality of the reals must be equal to both 2ℕ and the cardinality of P(ℕ), since the latter two are equal.
The first thing to note is that because ℕ is infinite, the result of the operation P(ℕ) is also infinite, i.e., it does not have a cardinality, since a cardinality is a fixed magnitude that represents the total number of elements in a set. P(ℕ), however, is always growing, i.e., it never stops increasing its number of elements, and so can never have a fixed cardinality which can be compared to the cardinality of another set. Also, as we have discussed in previous sections, P(ℕ) is countably infinite, because the elements in this set are simply individual sets that are subsets of the natural numbers. As such, each element in P(ℕ) can be mapped to a single number in the index sequence of natural numbers, and thus P(ℕ) is countable. Since according to the proof in Hrbacek the cardinality of the set P(ℕ) is supposed to be equal to 2ℕ, this would also mean that 2ℕ is countable – under the assumption, that is, that 2ℕ not be interpreted as an actual mathematical expression or operation. If we interpret 2ℕ simply as shorthand for “the number of unique infinite sequences of 0s and 1s,” then since each infinite sequence can be treated as a single element in the set of all such sequences, and since each such infinite sequence can be mapped to a single natural number, the number of elements in this overall set is also countable, i.e., 2ℕ is countable. Note that this is valid because even though there is an infinite number of numbers in each element, we are not setting this sequence of numbers equal to a fixed magnitude, which the diagonal argument does with its infinite decimal sequences, and which is logically flawed, but rather are treating each infinite sequence of 0s and 1s as a finite pattern, the pattern of “add another 1 or 0 to this particular element’s sequence of 0s and 1s,” and identifying the pattern with a particular natural number in the index sequence. In this way, for the purpose of enumerating these elements we may treat each one as a black box that looks exactly the same for all elements, and simply subscript the black box at a particular position in the index sequence with that position’s index sequence number, and this will do all that is needed to ensure that these unique infinite sequences are identified as unique for the purpose of indexing them, and thus for showing that only the natural numbers are needed to count them. This way of looking at things, in fact, makes it more plain that this set of sets is, in fact, countable, not uncountable. However, if we treat 2ℕ as an actual math problem, the problem of raising 2 to the power of the number of natural numbers, then the expression is nonsensical, because the process of exponentiation is only meaningful when both the base and the exponent are finite, i.e., fixed quantities. The naturals are infinite, and therefore are not finite and are never fixed in magnitude. The task of mathematically evaluating 2ℕ, therefore, is one that cannot logically be done, and so it makes no sense to try to compare the resulting “magnitude” or “value” with the cardinality of a set. If we rule out this latter impossibility, then we are left with the fact that both 2ℕ and P(ℕ) are countable, and, therefore, if any subsequent component of a proof were to find that the set ℝ has cardinality between 2ℕ and P(ℕ), this would prove not that ℝ is uncountable, but that ℝ is countable. In fact, the only reason we believe that either 2ℕ or P(ℕ) is uncountable is that the proof shows that ℝ is equal to them in total magnitude or number of entities and the diagonal argument has “shown” previously that ℝ is uncountable, meaning the other two must also be uncountable. However, if we understand that the diagonal argument is flawed, we lose the entire basis on which we conclude that 2ℕ and P(ℕ) are uncountable.
As a brief aside, we will also note that it is a false analogy to say that because the number of elements in the power set of a finite set is 2 to the power of the number of elements in the set, this must mean that the number of elements in the power set of a countably infinite set is 2 to the power of a countably infinite number of elements. This is to breach the bounds of applicability of the pattern that maps the number of elements in a set to the number of elements in its power set. The assumption is that because this relation holds for all n∈ℕ, it must also hold for ℕ itself as the “highest” of the natural numbers, i.e., this is an attempt to take the valid process of mathematical induction beyond the bounds of its applicability. If we can prove that a pattern holds for the first natural number, and also that if the pattern holds for n it must hold for n+1, then we have proven that this pattern holds for all the natural numbers. But because the natural numbers are infinite, and thus never end, it is impossible for this process to ever get to the point of the “highest” of the natural numbers, much less to go “above” or “beyond” the “end” of them; to conclude that this is the case is to conflate the finite with the infinite, and thus to make a logical error. In other words, “transfinite induction,” as we have discussed in a prior section, is a logical impossibility. But to be valid, the analogy must make recourse to transfinite induction. Thus, the analogy is flawed. The idea that the total number of subsets of the natural numbers, being equal to the total number of reals, could ever be greater in number than the total number of natural numbers is an artifact of the diagonal argument, which says that the number of reals is greater than the number of naturals. However, as stated above, if we understand that the diagonal argument is flawed, and that the reals are countable, no different from every other logically valid infinite set, then the idea that the total number of subsets of the naturals is “equal” to the total number of reals no longer lends credence to the idea that the total number of subsets of the naturals is greater than the total number of naturals themselves.
Hrbacek’s proof uses the idea of Dedekind cuts, which define real numbers (typically irrationals) as the limit points of infinite sequences of rationals approaching ever closer to them, but never reaching them. It is clear that a single real number, which is the fixed limit point itself, can be approached by more than one infinite sequence of rationals, and, in fact, by an infinite number of such sequences. Even without the fact that the power set of the rationals also includes all the finite sets of rationals, the argument can conclude from this that there are at least as many infinite sequences of rationals as there are reals. (Adding the finite sets of rationals does not alter this conclusion.) But there is some fuzziness here. In the realm of the finite, when two or more numbers in one set map to each number of a second set, and none of the mappings overlap, i.e., all numbers in the first set that map to a given number in the second set map to only that particular number in the second set and no other, we say that the first set is clearly greater in cardinality, or number of elements, than the second set. There is a certain recognition of this in the proof as well, by including a “greater than” component to the relationship between sequences of rationals and the reals, such that it appears, to all intents and purposes, that the number of infinite sequences of rationals is actually greater than the number of reals. But then we are forced to weasel a bit, because we also know that the number of infinite sequences of rationals is infinite, and we know that the number of reals is infinite, i.e., both of these sets are infinite. But since our understanding of infinity is flawed, we do not see clearly how to relate these two infinite sets, i.e., how to index or map between their elements. We, therefore, are stuck between a rock and a hard place. On the one hand, it seems clear that the number of infinite sequences of rationals is greater than the number of reals, but on the other hand both sets of numbers are infinite, and so we are left with a nagging uncertainty about whether what we think is clear actually is clear. We therefore play it safe and add an “equal to” component into the mix, to try to be as sure as possible that what we say is correct, and conclude that the number of reals is less than or equal to the number of infinite sequences of rationals (or, equivalently, that the number of such sequences is greater than or equal to the number of reals). By the same argument, therefore, the number of reals is less than or equal to the cardinality of the power set of the rationals. But, using the same argument as for the natural numbers above, we know that both the rationals and the power set of the rationals are countable. What this means is that the cardinality of the reals is less than or equal to the countable cardinality of the power set of the rationals, and thus the countable cardinality of the power set of the naturals. And since we know the reals are themselves infinite, this in itself is enough to prove, by the squeezing property, that the reals are countable. It should be noted here, as well, that to be strictly correct in this proof, we must interpret the “less than or equal to” component not to mean that the total number of reals is less than or equal to the total number of infinite sequences of rationals or naturals, since this would be to compare two infinities as if they were finite, fixed magnitudes, which is a logical contradiction. Rather, the “less than or equal to” component must be understood to only have meaning in the sense that a particular real number maps to at least two infinite rational sequences, and that this is the case for every single real. The fact that “one” real can always be mapped to “more than one” infinite sequence of rationals, and that none of the infinite sequences of rationals need map to more than one real, is enough to allow for the “less than” component to be logically valid, since, as with quantifying over the entirety of the natural numbers in first-order logic, a particular, concrete “less than” evaluation is only ever performed on finite numbers. We may then add the “equal to” component into the mix in recognition that the reals and the set of infinite sequences of rationals are both infinite. But then, we may drop the “less than” component after further recognition that since these two sets are both infinite, they must both be countably infinite, since there is no such thing as uncountable infinity, and this leaves only an equal sign between the two sides. Finally, we must ensure that we do not interpret this equal sign as saying that the two sets have the same number of elements, since this would imply that fixed cardinalities are being compared, which would be a logical contradiction since the two sets being compared are infinite; rather, we must interpret the equal sign only as saying that both sets have the particular attribute of being countable. In this way, we have provided a valid proof that the reals are countable, though technically some of these elements are unneeded for such a proof.
But the proof in Hrbacek continues a little further. Let us analyze this last part of their proof. In this part of the proof, they make each infinite sequence of 0s and 1s equal to an infinite decimal sequence that represents a real number in the interval (0, 1); specifically, these decimal sequences map into, but not onto, (0, 1). But since these sequences only map to a part of the real line, the total number of these sequences, which is 2ℕ, would seem to clearly be less than the total number of reals. Again, this would be the clear conclusion drawn in the realm of the finite. But because we are dealing with two infinite sets, the collection of all infinite sequences of 0s and 1s as well as the set of all reals, there creeps in a nagging uncertainty about what at first glance seems like it should be clear and definitive. Therefore, because both sets are infinite, we weasel a bit, and, instead of saying that the cardinality of the set of infinite sequences of 0s and 1s is strictly less than that of the set of reals, we say that the former is less than or equal to the latter. The “equal to” component reflects our lack of certainty regarding the actual relationship between the cardinalities of these sets. But by representing the relevant subset of the reals by infinite decimal sequences, we obscure the nature of what we are discussing, and make it harder to see the truth of the matter, or, equivalently, easier to draw a false or logically meaningless, but emotionally pleasing, conclusion. Because we are so accustomed to equating infinite decimal sequences with their finite limit points, by using infinite decimal sequences we hide the fact that in this part of the argument we are no longer talking about real numbers; that is, each infinite decimal sequence is meant, as in the diagonal argument, to be equal to a real number, but an infinite decimal sequence can never be equal to a real number, because the former never completes and is thus always changing, while the latter is always complete and thus never changes. These two things are the opposite of each other in this essential respect, and it is thus logically contradictory to equate them. But each such infinite decimal sequence approaches, and thus maps to, a single, fixed real number, and as such what each infinite decimal sequence is supposed to represent can be mapped one-to-one with a particular natural number. But because the natural numbers are infinite, and thus never end, then we may map to the naturals as many of the reals that these infinite decimal sequences represent as we like, in addition to as many of the other reals as we like beyond what are represented by the infinite sequences of 0s and 1s, and this process will never have an end, i.e., will never be complete. The idea that a number of elements equal in cardinality to 2ℕ is able to be mapped into a tiny portion of the real line ignores the fact that the expression 2ℕ, if we are to interpret it in a meaningful way, means countable infinity, and thus it is impossible to “complete” a mapping of this many elements in one-to-one correspondence with real numbers, so that we may then go “beyond” this completed mapping to consider the “rest” of the real numbers. It is not appropriate, to any degree, to say that 2ℕ is “less than” the cardinality of the reals, because this implies (a) that an infinity can be compared in terms of magnitude to another magnitude, and (b) that different infinite sets can have different sizes, which is the only way “less than” would have any applicability when comparing different infinite sets. But both of these assumptions are flawed, and thus not correct. The only meaningful way to say that a set has 2ℕ elements is to say that it is a countably infinite set. And since the reals are themselves individual, fixed magnitudes, which can thus be mapped one-to-one with the natural numbers, the reals are also countably infinite. It is, therefore, correct to say that a set with 2ℕ elements and the set of the reals are equal, in the sense that they are both countably infinite. The idea that an infinite set of elements can be mapped to a small section or set of points on the real line is an artifact of conflating the finite with the infinite, specifically the erroneous conclusion that a sequence of zero-length positions representing real numbers lined up can ever produce a sum total length greater than 0. We recognize that the fixed real numbers that are the limit points of the infinite sequences of 0s and 1s are zero-length points or positions on the real line, and we know that there is an infinite number of such sequences, but then at the same time we erroneously assume that a continuous geometric line can be built up out of a sufficient number of these zero-length points, so that in a certain way it makes sense to use the “less than” relational component in our conclusion about the relationship between 2ℕ and the cardinality of the reals. It is the same with the relation of the naturals to the reals when they are thought of a positions on the real line. The naturals are fixed, equidistant points on the real line, and it is clear that there are numbers that are in between any two successive such fixed points. Based on this, it would seem clear and definitive that the number of reals is greater than the number of naturals. However, we then run into difficulty with the fact that the naturals and the reals are both infinite sets, so, in the absence of other information about how these two sets relate to each other, we must play it safe and say that the naturals are merely less than or equal to the reals in terms of cardinality. Here, the diagonal argument confuses things by lending credibility to the erroneous idea that the reals are greater in cardinality than the naturals, and thus to the conclusion that “of course” this makes sense when looking at the geometric line that is supposed to be built up solely out of the complete set of real numbers, and that in this representation of the reals and their relationship to the naturals there seems to be “something true” that is showing itself, of which truth the diagonal argument serves as a sort of independent confirmation. But as we have seen, no amount of zero-length points can ever amass linearly to any length greater than 0, so how is it possible to create such a line to begin with in order to compare the reals and the naturals in this way? Ultimately, these are all inherently unclear notions, and there is no possible way to shed light on these matters other than to recognize that it is a logical error to conflate the finite with the infinite, and then to trace the implications of this recognition.
Another comment can be made with regard to the “less than or equal” components of the proof. We have said that it is uncertainty with regard to the choice between the “less than” and “equal to” relations that forces us to specify the “less than or equal” relation in the comparison of the three different “numbers.” If we look more closely at the reason why we have this uncertainty, we will find that it is not because the relation in question is one or the other and we simply do not have enough knowledge to determine which of the two it is. Rather, it is because we are attempting to compare finitized infinities, i.e., logically contradictory entities, and a consequence of this is that one such entity can be both less than another and equal to it at the same time. We see, for example, that the number of infinite rational sequences is greater than the number of reals, since each real can be mapped to by more than one unique infinite rational sequence, but at the same time the number of reals and the number of infinite rational sequences are both infinite, and can each thus be mapped one-to-one with the natural numbers (however much we try to tell ourselves that this is not the case for the reals), meaning they are both countably infinite, and thus both “equal” in terms of cardinality. Each of these situations seems to have an essential element of truth to it. But, of course, logically it cannot be true that one number is both equal to another number and at the same time less than it. Since we do not have a clear understanding of infinity, and thus still think that the comparisons we are making between finitized infinities are logically valid, then the only conclusion that we can draw from this state of affairs is that the one number is less than or equal to another. But in fact, since this uncertainty, this confusion, is the result of the treating of a logical error as if it is not a logical error, and since logically erroneous conclusions are drawn from logically erroneous premises, it makes more sense to conclude, for each of the two comparisons, that the one finitized infinity is “less than and equal to” the other.
In discussing the limitation of size principle, which is a way to try to categorize collections of elements by whether or not the property that determines the elements of the set is collectivizing, Potter states, “Cantor [called] a cardinality absolutely infinite if it is too large for that number of objects to be collected together. It is easy to see how the very attempt to collect so many things together could be presented as an instance of that recurrent theme of human folly – hubris in the face of the incomprehensible… . [But while the ancient Greeks] had identified the Absolute with the infinite, … Cantor now proposed to split them apart so that on his account there would be cardinalities which are infinite but not absolutely infinite (hence are comprehensible by human thought)… . [For the constructivist explanation of limitation of size,] what is [perhaps] required is that we should run through the objects in our thought. If so, it is easy to see why pre-Cantorians identified the absolutely infinite with the simply infinite, since it is by no means clear how a finite being – even an idealized one – is expected to be able to run through an infinity of things. To make any sense of this, we have to be willing to accept the coherence of the notion of a supertask.”195 Cantor did not understand that there is no difference between countable and uncountable infinity. It is not possible for there to be an “infinite cardinality” that is so high that a number of objects representing that cardinality could not be collected together, while at the same time the number of objects of infinite cardinalities below this level can all be collected together. The point of infinity is that we may collect as many objects as we like together, and the only thing that could ever be done is to add, in a countable way, ever more elements to the finite collection that we have built so far at any given point. There is no limitation of size that would serve as a fundamental or logical dividing line between infinite sets whose elements can be collected together and infinite sets whose elements cannot. In no case of an infinite set can the entirety of its elements be collected together. The idea that the infinite could be separated into a “lower” and a “higher” level of infinity in the first place is due to the flawed belief that there are different levels of infinity, a belief which Cantor wanted to be true. Countable infinity is comprehensible by human thought, because it is produced by patterned behavior. In addition, the only type of infinity is countable infinity. Therefore, infinity itself is fully comprehensible by human thought, since we are able to understand patterned behavior. This does not mean that we have fully circumscribed or completed or finitized infinite sequences of elements. It just means that the concept of countable infinity is a logically valid concept, i.e., its definition does not contain any logical contradictions. Potter states, “Cantor’s idea [was] that the universe of sets in some way represents the Absolute, and hence that it would be a sort of blasphemy to suppose that a finite being could express it.”196 Cantor had a deep emotional need to prove that his God exists, and to thereby wrap his hands around eternity: “As an orthodox Lutheran, Cantor viewed God as all wise, all powerful [and] infinite … . He believed God had blessed him with profound insights concerning infinity and had commissioned him as a prophet to proclaim this message to others… . [Cantor wrote such things as] ‘Every extension of our insight into the origin of the creatively-possible therefore must lead to an extension of our knowledge of God’ and ‘I am so in favor of the actual infinite that instead of admitting that Nature abhors it, as is commonly said, I hold that Nature makes frequent use of it everywhere, in order to show more effectively the perfections of its Author.’”197 But one cannot wrap one’s hands around eternity, i.e., finitize the “ultimate infinity” (while at the same time paradoxically saying that because God is God it is impossible for humans to do so), if the only conception of the infinite one has is the countably infinite, since, after all, humans are capable of understanding the countably infinite by means of our inherent capacity to understand patterned behavior, and since this understanding, if not quickly made less plain by conceptual twisting and distortion, forces us to realize in a blatant and undeniable way that infinity is infinite, and thus cannot ever be grasped in its entirety. God, on the other hand, is supposed to be, at least in some sense, beyond human understanding. What good is a God that is entirely comprehensible to the human mind? Such a God would serve no useful purpose to the human psyche, precisely because the concept of God is useful only as a conceptual tool to help us believe we can overcome death, i.e., that somehow it is possible for us to eventually move into an eternity that as mortals is not fully comprehensible to us. What we are able to comprehend, i.e., what we can conceive rationally, is always a pattern, and thus always finite. Our psyches, in a crude but powerful emotional way, seek to overcome the finiteness of life by finding a way to conquer death. If we are to overcome finiteness in this essential way, then our conception of the infinite cannot be one that is fully comprehensible to us, because as soon as we comprehend it we realize we have not solved the problem of overcoming finiteness in our lives, since even though we now understand infinity, we, of course, are still going to die. This is the same reason that religions tend to define their concepts and beliefs in ways that purposely place their most essential constructs, beings, realms, etc., either partially or fully beyond the realm of rational inquiry and criticism, so that they will be safe from such harsh, unflattering light. If, in set theory, we purposely define a level of infinity that is fundamentally beyond the ability of human capacity to grasp, which definition is motivated by a fortuitously germane mathematical argument, then we have done exactly the same thing, just in a more appropriately scientific or intellectual outward format, and thus a format that in intellectual circles is more respectable, not to mention a format that insightful and rationally-minded people such as Cantor need to place it in, in order to feel as though what they wish to believe about God or about the world actually could be true. What such a definition of infinity does is give us the best of both worlds – we have, or at least feel as though we have an at least somewhat concrete path to, the ability to finitize infinity, but at the same time we do not have to directly face the fact that infinity, being infinite, is inherently unfinitizable, since our chosen conception of infinity is inherently opaque and thus does not force us into direct confrontation with this unpleasant reality.
For Cantor, the transfinite in set theory was an essential part of his effort to understand the foundations of the world, and, thereby, to glorify God and teach His revelations, and so the “universe of sets” was in his mind an essential component of the universe, of its foundation, its creation. And if this “perfect completion” at the foundations of the world exists, and if God also exists, then it seems reasonable to equate the two in some way. But this effort at finding or reaching “perfect completion” is no different from the effort to equate a non-terminating decimal sequence with its limit point, or to equate the successor function with the infinite sequence which it produces. “Absolute infinity” is nothing but a way of expressing the concept of limit points of logically comprehensible infinite sequences, where we may move ever in the direction of a limit point but never actually reach it. Cantor, in other words, superimposed actual infinity, that is, countable infinity, onto the sequence of uncountable cardinals, and in this way disguised to himself the fact that his “absolute infinity” was nothing more than an unnecessarily complicated expression of the fact that countable infinity never ends. Cantor also is guilty of conflating the finite with the infinite in thinking that the limit point of “absolute infinity” actually exists as a completed totality, albeit one that humans could supposedly never comprehend. But this itself is a contradiction, because if it exists as a completed totality, then like any and every uncountable ordinal or cardinal, it now becomes possible to move one step beyond it, which means that it is no more “absolute” an infinity than countable infinity, or than any of the uncountable infinities in any sequence of uncountable transfinite numbers. Potter is correct in saying that our attempt to collect an infinite number of things together is an example of human hubris, though it is not strictly, that is, not necessarily, hubris in the face of the incomprehensible. For many who may attempt to do this type of collecting, such an aspect of reality may actually be incomprehensible to them. But this is not true for everyone, i.e., it is not constitutively true for the human psyche in general, and this means that the concept of the infinite, when properly understood, is not fundamentally beyond the human brain’s capacity to comprehend. The idea that it is or that it might be, or that a part of it might be, is an indirect and distorted reflection of the sneaking suspicion in our minds that we, in fact, are not able to actually solve the problem of death, that the infinite will forever be beyond our full grasp in certain essential ways. But by simply thinking a little about the actual definition of “infinite,” and how it relates to “finite,” we will find that it is possible to understand what “infinite” is, as is the case for any word whose definition does not contain a logical contradiction. We should add also that it is not just hubris, or an inflated sense of our own capacities or abilities, that makes us think we can finitize the infinite, but also desperation, however indirect and masked to ourselves, to find a way to avoid mortality, which desperation serves as a continually-renewing spring of mental creativity and energy aimed at keeping us as blind as possible to our own insignificance and transience, and as focused as possible on building and maintaining an image of ourselves as special, consequential, and eternal. In fact, the need to overcome mortality is the source for both the hubris and the desperation, and the hubris is an outgrowth of the desperation.
Potter comments, “Part of what makes large cardinals so hard to accept is precisely the Cantorian finitism which has sometimes been used to motivate them. This is the idea that infinite sets are, as far as possible, just like finite sets. If we adopt this idea, we are encouraged to regard the claim that a large cardinal is much bigger than, say, 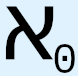 as having the same sort of import as the claim that 1020 is much bigger than 12. But if we do that, do we lose our grip on reality? Do we, as Boolos has suggested, ‘suspect that, however it may have been at the beginning of the story, by the time we have come thus far the wheels are spinning and we are no longer listening to a description of anything that is the case?’ ”198 In fact, this is the same stance that has been taken throughout this paper, viz., that there is no inherent meaning in the idea of uncountable infinity or the transfinite, and that countable infinity itself is not fully correctly expressed in modern set theory. The “as far as possible” part of the comment gives much-needed wiggle room to any set theorist or philosopher who wishes to superimpose finiteness onto the infinite so as to bring the infinite into the realm of the finite, which wiggle room is needed because such superimposing creates a contradiction, so no matter how the ideas are massaged there will always be an intractable irreconcilability involved in this conflation that will express itself in a variety of ways, and in ways that depend on the idiosyncrasies of the particular set theory, or model, or philosophical stance, etc., in question. As we have seen, only countable infinity exists, and the way to accommodate this in set theory is simple, and in certain indirect ways has already been done. If, on the other hand, we strike out beyond this point, we pass into the realm of logical error, and so of course the ideas we conceive after this point do not accurately reflect reality.
as having the same sort of import as the claim that 1020 is much bigger than 12. But if we do that, do we lose our grip on reality? Do we, as Boolos has suggested, ‘suspect that, however it may have been at the beginning of the story, by the time we have come thus far the wheels are spinning and we are no longer listening to a description of anything that is the case?’ ”198 In fact, this is the same stance that has been taken throughout this paper, viz., that there is no inherent meaning in the idea of uncountable infinity or the transfinite, and that countable infinity itself is not fully correctly expressed in modern set theory. The “as far as possible” part of the comment gives much-needed wiggle room to any set theorist or philosopher who wishes to superimpose finiteness onto the infinite so as to bring the infinite into the realm of the finite, which wiggle room is needed because such superimposing creates a contradiction, so no matter how the ideas are massaged there will always be an intractable irreconcilability involved in this conflation that will express itself in a variety of ways, and in ways that depend on the idiosyncrasies of the particular set theory, or model, or philosophical stance, etc., in question. As we have seen, only countable infinity exists, and the way to accommodate this in set theory is simple, and in certain indirect ways has already been done. If, on the other hand, we strike out beyond this point, we pass into the realm of logical error, and so of course the ideas we conceive after this point do not accurately reflect reality.
To conquer the infinite is to do just about the greatest thing that anybody might think to do. Of course, set theory is not just about conquering the infinite, but also about providing a foundation for mathematics. But the goal of mathematics is to understand the basic principles by which the world operates, i.e., to understand, and thus conceptually circumscribe, the patterns underlying existence and change; and this desire to conceptually finitize the world has its roots in the need to survive within it. Different people express the need to survive in different ways, some by becoming academics, either officially or unofficially, out of a desire to understand the world rationally at a deeper level than that required for day-to-day practical survival and navigation. The prospect of solving problems, answering questions, gaining and creating knowledge, playing a nontrivial part in driving humanity upward and outward – these are the signposts on our particular path toward happiness, fulfillment, contentment, inner peace. However, there is always still the deeper struggle between acknowledging the truth about things, especially foundational things, which ultimately leads to a full and non-repudiable acknowledgment of our own mortality, and preserving the illusion that we are immortal by finding acceptable ways to ensure that the world, at least at certain levels, remains mysterious. The struggle is particularly pronounced in philosophy, because this endeavor actively seeks to know the grand patterns of the world, though the severity of the struggle can be ameliorated by specializing.199 But the more foundational ideas tend to cross the borders of different specialties, uniting them and bringing both clarity to their interrelationships and an understanding of the relative significance of each to the larger set of ideas. Foundational ideas are nearer to the ultimate level of logical necessity than non-foundational ideas, and so the pursuit of foundational ideas brings one closer to understanding truths from which there is no escape, because such truths apply universally. But just for this reason, the understanding of such truths is worth the struggle and disillusionment, because it frees us to think more creatively, achieve more profoundly, live more fully. The universe exists, it is as it is, and we are here at a specific spot within its immensity. How amazing is that? Let us make the most of it.